
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды коэффициентов корреляций и их применениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Корреля́ция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин. Математической мерой корреляции двух случайных величин служит корреляционное отношение Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и ее направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин. В силу сложности, многофакторности общественной жизни связи между социальными переменными практически всегда корреляционные. Количественно они описываются с помощью коэффициентов корреляции. В случае корреляционной связи между признаками х и у каждому значению одной величины (x i) соответствует групповая средняя другой (y i). Уравнения, описывающие эту зависимость, называются корреляционными, или регрессионными, а соответствующие им графики – кривыми регрессии. Коэффициенты корреляции– меры плотности корреляционной связи. Когда каждому значению одного признака соответствуют различные, но близкие значения другого признака, т.е. тесно располагающиеся около своей средней величины, – связь более плотная. Коэффициент Пирсона-Бравеявляется r мерой связи при линейной корреляции. Все его значения заключены между – 1 и + 1, причем крайние значения соответствуют линейной функциональной связи между признаками. Значенне r=0 означает отсутствие линейном связи, но при r=0 может иметь место нелинейная связь, даже функциональная. Мерой плотности нелинейной связи является корреляционное отношение R, принимающее значение между 0 и 1. Значение 0 соответствует отсутствию связи. Чем больше R, тем теснее связь между признаками. Значение 1 соответствует функциональной связи. Модуль r всегда не превосходит R (для одной и той же корреляционной таблицы), r и R применяются для описания количественных признаков. Если при описании объектов удается определить лишь наличие или отсутствие у них признака, либо если изучается связь между альтернативными признаками, то корреляционные таблицы становятся четырехклеточными. В таких случаях можно применять коэффициенты ассоциации и контингенции. Ряд коэффициентов корреляции основан на критерии Пирсона. Это коэффициент сопряженности Пирсона, теоретически более предпочтительный коэффициент Чупрова. Коэффициенты частной корреляции позволяют изучать связи между признаками при элиминировании влияния некоторых других признаков. Если устраняется влияние одного признака, то говорят о частных коэффициентах корреляции первого порядка. Они выражаются через обычные коэффициенты парной корреляции. Логика частной корреляции такова: если при устранении некоторого признака коэффициент корреляции двух данных признаков увеличивается, то такой признак ослабляет связь, если же коэффициент корреляции уменьшается, то устраняемый признак в определенной мере обуславливает связь. (В предельном случае, если устранение признака обращает коэффициент корреляции в нуль, то данный признак обуславливает связь данных признаков, т.е. это связь сопутствия). Например, при изучении корреляции между производительностью труда и возрастом рабочих была установлена положительная связь. На производительность влияет и стаж работы, который оказывается в положительной корреляции и с возрастом, и с производительностью. При элиминировании стажа оказалось, что связь между производительностью и возрастом отрицательная, а между производительностью труда и стажем (при элиминировании возраста) –положительная и еще более тесная. Если устраняется влияние двух признаков, то говорят о частных коэффициентахкорреляции второго порядка. Они в свою очередь выражаются через коэффициенты частной корреляции первого порядка и т.д.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1535; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.248.214 (0.005 с.) |

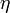 , либо коэффициент корреляции
, либо коэффициент корреляции 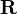 (или
(или  ). В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.
). В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.


