
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С помощью коэффициента парной корреляцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Допустим, проводится независимое измерение различных параметров у одного типа объектов. Из этих данных можно получить качественно новую информацию – о взаимосвязи этих параметров. Например, измеряем рост и вес человека, или рост и размер обуви. Каждое измерение представлено точкой в двумерном пространстве:
Несмотря на то, что величины носят случайный характер, в общем, наблюдается некоторая зависимость – величины коррелируют. В данном случае это положительная корреляция (при увеличении одного параметра второй тоже увеличивается). Возможны также такие случаи:
Рис. 5 Рис.6 Связь между величинами может быть и нелинейной (рис. 7).
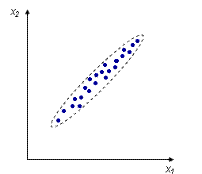
Взаимосвязь между переменными необходимо охарактеризовать численно, чтобы, например, различать случаи, приведенные на рис.8 и рис.9.
Рис. 8 Рис. 9 Все, что мы видим на приведенных выше рисунках, называют диаграммой рассеивания. Если облако точек напоминает очертания некоторой линии, то можно предполагать, что мы видим на диаграмме рассеяния именно такую по форме зависимость, однако искаженную воздействием как случайных, так и неучтенных факторов, вызывающим отклонение точек от теоретической формы. Поскольку наиболее простой формой в математике является прямая пропорциональная зависимость, то в корреляционном и регрессионном анализе наиболее популярны линейные модели. Для численных оценок вводится коэффициент корреляции (коэффициент парной корреляции)
Коэффициент корреляции Коэффициент парной корреляции вычисляется для количественных признаков. Коэффициент корреляции симметричен, т.е. не изменяется, если X и Y поменять местами, и является величиной безразмерной. Коэффициент корреляции не изменяется при изменении единиц измерения признаков X и Y. Сам по себе коэффициент корреляции не имеет содержательной интерпретации. Однако его квадрат (r2), называемый коэффициентом детерминации (обозначается d и обычно выражается в %), имеет простой смысл – это показатель того, насколько изменения зависимого признака объясняются изменениями независимого. Более точно, это доля дисперсии (разброса) одного признака, объясняемая влиянием другого (если связь интерпретировать как причинно-следственную). Из определения коэффициента детерминации следует, что он принимает значения в диапазоне от 0% до 100%. Если две переменные функционально линейно зависимы (точки на диаграмме рассеяния лежат на одной прямой), то можно сказать, что изменение одной из них полностью объясняется изменением другой. Это как раз тот случай, когда коэффициент детерминации равен 100% (при этом коэффициент корреляции может быть равен как 1, так и –1).
Коэффициенты корреляции и детерминации Если две переменные линейно независимы (метод наименьших квадратов, о котором пойдет речь в следующем параграфе, дает горизонтальную прямую), то одна из них в своих изменениях никоим образом не определяет другую – в этом случае коэффициент детерминации равен нулю. В остальных случаях коэффициент детерминации указывает, какая часть изменений одной переменной объясняется изменениями другой переменной. Чем выше по модулю (по абсолютной величине) значение коэффициента корреляции, тем сильнее связь между признаками. Принято считать, что коэффициенты корреляции, которые по модулю больше 0,7, говорят о сильной связи (при этом коэффициенты детерминации > 50%, т.е. один признак определяет другой более чем наполовину). Коэффициенты корреляции, которые по модулю меньше 0,7, но больше 0,5, говорят о связи средней силы (при этом коэффициенты детерминации меньше 50%, но больше 25%). Наконец, коэффициенты корреляции, которые по модулю меньше 0,5, говорят о слабой связи (при этом коэффициенты детерминации меньше 25%). Оценить глубину корреляционной связи и характер связи можно, пользуясь табл. 2: Таблица 2.
Если Методами корреляционного анализа решаются задачи: 1. Взаимосвязь. Есть ли взаимосвязь между параметрами? 2. Прогнозирование. Если известно поведение одного параметра, то можно предсказать поведение другого параметра, коррелирующего с первым. 3. Классификация и идентификация объектов. Корреляционный анализ помогает подобрать набор независимых признаков для классификации.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

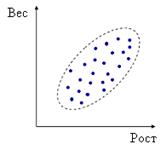


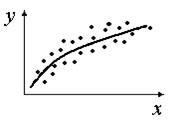 Рис. 7
Рис. 7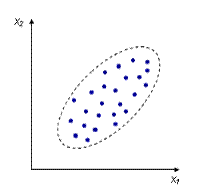
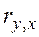 . Для линейной связи переменных он рассчитывается по формуле Пирсона.
. Для линейной связи переменных он рассчитывается по формуле Пирсона.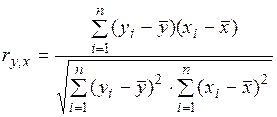
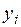 и xi. Коэффициент корреляцииравен 1 (или -1), если связь линейна.
и xi. Коэффициент корреляцииравен 1 (или -1), если связь линейна.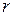
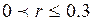
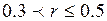


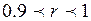
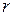 >0, то связь прямая (положительная), при
>0, то связь прямая (положительная), при 


