
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи на составление дифференциальных уравнений.Содержание книги
Поиск на нашем сайте Рассмотрим конкретный пример. Скорость распада радия пропорциональна его имеющемуся количеству R. Найти закон распада радия, если известно, что через 1600 лет останется половина первоначального количества. Какой процент радия окажется распавшимся через 100 лет? Решение. Пусть R - количество радия в момент времени t, а R 0- его первоначальное количество. Тогда скорость распада радия равна
Осталось найти k и C. Для определения произвольной постоянной С воспользуемся начальным условием: R=R 0 в начальный момент времени t =0. Тогда R 0= С. Итак, закон распада радия имеет вид
Для нахождения k воспользуемся следующим условием:
Таким образом, окончательно получаем
При t=100 имеем
Следовательно, через 100 лет распадается 4,2% первоначального запаса радия.
Решить задачи. 6.26. Тело за 10 мин охлаждается от 100 до 60° С. Температура окружающего воздуха равна 20° С. Считая скорость остывания тела пропорциональной разности температур тела и окружающего его воздуха, определить, за какое время тело остынет до 30° С. Указание. Пусть Т - температура тела в момент времени t. Тогда дифференциальный закон охлаждения тела имеет вид
6.27. Моторная лодка движется в спокойной воде со скоростью 1,5 м/с. Через 4с после выключения мотора ее скорость уменьшилась до 1 м/с. Считая, что сопротивление воды пропорционально скорости движения лодки, найти ее скорость через 50с после остановки мотора. Указание. Пусть V - скорость лодки после выключения мотора в момент времени t. Тогда зависимость между V и t имеет вид
6.28. Поглощение светового потока тонким слоем воды пропорционально толщине слоя и потоку, падающему на его поверхность. При прохождении через слой толщиной 2м поглощается 1/3 первоначального светового потока. Определить, какой процент первоначального светового потока дойдет до глубины 4м. Указание. Пусть Q - световой поток, падающий на поверхность на глубине h. Тогда dQ = - kQdh.
6.29. Скорость тела V, брошенного вниз с начальной скоростью V 0, определяется равенством V = V 0+ gt. Найти уравнение движения данного тела.
6.30. Скорость размножения некоторых бактерий пропорциональна начальному количеству бактерий. Найти зависимость изменения количества бактерий от времени.
6.31. Найти закон роста клеток с течением времени, если для пальчиковых клеток скорость роста
6.32. По какому закону происходит разрушение клеток в звуковом поле, если скорость их разрушения пропорциональна начальному количеству N.
6.33. Скорость укорочения мышц описывается уравнением
Глава 7 Элементы теории вероятностей И математической статистики
Основные понятия
Теория вероятности и методы математической статистики широко используются при изучении заболеваемости, физического развития населения, физиологических и биохимических показателей. Это обусловлено тем, что многим биологическим явлениям свойственны статистические закономерности, которые обнаруживаются при изучении случайных совокупностей. Теория вероятностей изучает закономерности, присущие массовым (статистическим) случайным событиям, и их количественную оценку. Математическая статистика позволяет систематизировать и оценивать экспериментальные данные, которые рассматриваются как случайные величины. Важнейшими понятиями теории вероятности и математической статистики являются понятия: «случайное событие», «вероятность случайного события», «случайная величина». Случайным событием А называют событие, которое в одинаковых условиях эксперимента может произойти, а может и не произойти, и о появлении которого не может быть сделано точного предсказания.
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 2426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.009 с.) |

 и является отрицательной величиной, т.к. R с течением времени убывает. Согласно условию задачи имеем:
и является отрицательной величиной, т.к. R с течением времени убывает. Согласно условию задачи имеем: 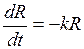 , где k >0 - коэффициент пропорциональности, подлежащий определению. Интегрируем полученное уравнение:
, где k >0 - коэффициент пропорциональности, подлежащий определению. Интегрируем полученное уравнение:

 при t=1600. Отсюда
при t=1600. Отсюда


 .
.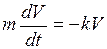 , где m- масса лодки.
, где m- масса лодки. пропорциональна длине клетки l в данный момент. Указание. Пусть
пропорциональна длине клетки l в данный момент. Указание. Пусть  , где a,b- постоянные, характеризующие процессы синтеза и распада.
, где a,b- постоянные, характеризующие процессы синтеза и распада. , где х 0- полное укорочение, х - укорочение в заданный момент. Найти закон сокращения мышц, если при t =0 величина укорочения была равна нулю.
, где х 0- полное укорочение, х - укорочение в заданный момент. Найти закон сокращения мышц, если при t =0 величина укорочения была равна нулю.


