
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одной независимой переменнойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Понятие производной Пусть Производной от функции
Или
Примечание. Производная обозначается также как Отыскание производной называется дифференцированием функции. Исходя из определения производной, можно найти производную любой дифференцируемой функции. Рассмотрим несколько примеров. 1. Найти производную функции
Дадим
отсюда
Функция
= Находим отношение приращения функции к приращению аргумента:
Найдем предел этого отношения при
Следовательно, по определению производной
2. Найти производную функции
Находим приращение функции
Таким образом,
Итак,
3. Найти производную функции
Находим приращение функции
Воспользуемся формулой
Отсюда
и
Итак,
Исходя из определения производной, найти производные следующих функций:
Основные правила дифференцирования. Дифференцирование основных элементарных функций. Основные правила дифференцирования Пусть C –постоянная, 1. 2. 3. 4. 5. Таблица производных основных элементарных функций
Применяя формулы и правила дифференцирования, найдем производную функции:
Запишем данную функцию следующим образом:
Тогда
В качестве следующего примера найдем производную от функции
Для нахождения производной воспользуемся правилом нахождения производной от произведения двух функций:
И, наконец, рассмотрим еще один пример: нахождение производной частного от деления двух функций
Для нахождения производной воспользуемся пятым правилом из раздела «Основные правила дифференцирования». Тогда
Найти производные следующих функций:
Дифференцирование сложной функции.
Пусть
Это правило распространяется на цепочку из любого конечного числа дифференцируемых функций: производная сложной функции равна произведению производных функций, ее составляющих. Рассмотрим несколько примеров нахождения производной сложной функции. Пример 1.
Положим Тогда
Пример 2.
Обозначим По правилу дифференцирования сложной функции имеем:
Пример 3.
Обозначим По правилу дифференцирования сложной функции имеем:
Пример 4.
Положим
Пример 5.
Если
Пример 6.
Положим Получаем
Пример 7.
Если
Пример 8.
Имеем
Найти производные следующих сложных функций:
Производные высших порядков Производная второго порядка (вторая производная) от функции
Производная третьего порядка (третья производная) от функции
Вообще производная n-го порядка (n-я производная) функции Рассмотрим пример. Найти третью производную от функции Дифференцируя данную функцию, получим
Найти производные второго порядка от функций:
Найти производные третьего порядка от функций:
Дифференциал функции
Дифференциалом (первого порядка) функции Дифференциалом аргумента называется приращение этого аргумента: Дифференциал функции равен произведению ее производной на дифференциал аргумента:
Основные свойства дифференциала.
1. 2. 3. 4. 5. 6.
Если приращение аргумента Дифференциалом второго порядка функции Используя определение дифференциала, рассмотрим ряд примеров. 1. Найти приращение Имеем
Найдем дифференциал функции:
Абсолютная погрешность
Относительная погрешность
2. Найти дифференциалы первого и второго порядков функции Имеем
3. Вычислить приближенное значение Рассмотрим функцию
4. Вычислить приближенное значение площади круга, радиус которого равен 3,02 м. Воспользуемся формулой
Следовательно, площадь круга радиуса 3,02м имеет приближенное значение
5. Вычислить приближенно Рассмотрим функцию Тогда, воспользовавшись формулой найдем
Таким образом, 6. На сколько увеличилось ребро куба, если объем его изменился с 27 м3 до 27,2 м3? Если Приращение
Найти дифференциалы следующих функций:
Найти дифференциалы первого, второго и третьего порядков.
2.149. Найти приращение и дифференциал функции 2.150. Вычислить | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

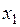 и
и 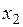 - два значения аргумента, а
- два значения аргумента, а 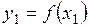 и
и 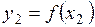 - соответствующие значения функции
- соответствующие значения функции 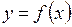 . Тогда разность
. Тогда разность 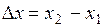 называется приращением аргумента, а разность
называется приращением аргумента, а разность 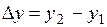 =
= 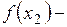
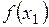 - приращением функции на отрезке
- приращением функции на отрезке 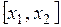 .
.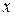 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
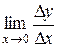
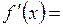
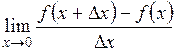
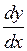 (Читается «дэ игрек по дэ икс».) Штрихом производная обозначается только в том случае, если она берется по
(Читается «дэ игрек по дэ икс».) Штрихом производная обозначается только в том случае, если она берется по 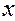 .
.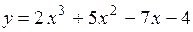 (1)
(1) , тогда
, тогда  получит приращение
получит приращение 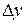 :
: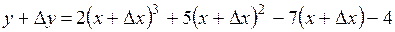 ,
,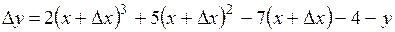 .
.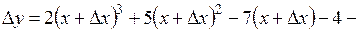
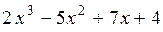 =
=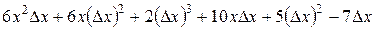
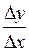 =
= 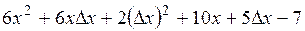 .
.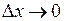 :
: =
= 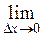 (
(
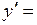
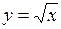 (2)
(2)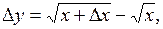 отсюда
отсюда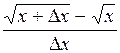 и
и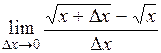
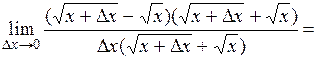

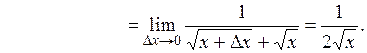

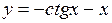 (3)
(3)
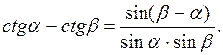
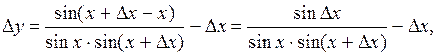
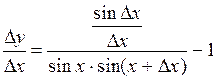
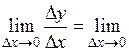
 =
= 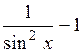 .
.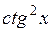
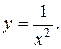 (Ответ: -
(Ответ: - 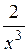 )
)
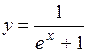 (Ответ:
(Ответ: 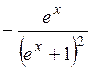 )
)
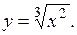 (Ответ:
(Ответ: 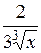 )
)
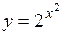 . (Ответ:
. (Ответ:  )
)
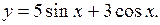 (Ответ:
(Ответ:  )
)
 .
(Ответ:
.
(Ответ: 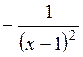 )
)
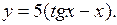 Ответ:
Ответ:  )
)
 .
(Ответ: 6(x-1))
.
(Ответ: 6(x-1))
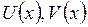 - функции, имеющие производные, тогда:
- функции, имеющие производные, тогда: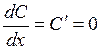
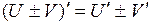
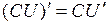
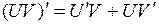

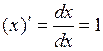
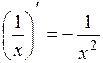
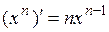
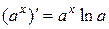
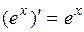
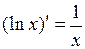

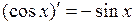
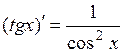
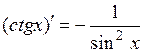
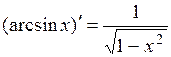
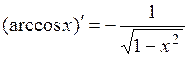
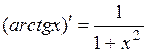
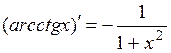

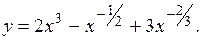

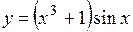 .
.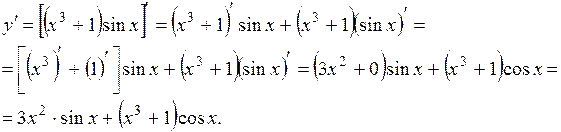
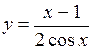 .
.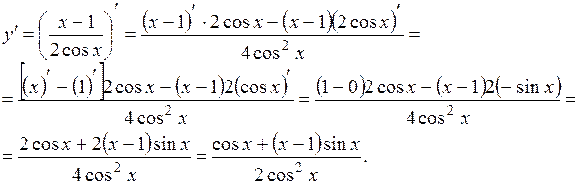
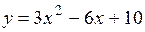 .
(Ответ: 6(x-1))
.
(Ответ: 6(x-1))
 .
(Ответ:
.
(Ответ: 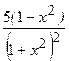 )
)
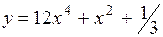 .
(Ответ: 2x(24x2+1))
.
(Ответ: 2x(24x2+1))
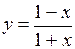 .
(Ответ:
.
(Ответ: 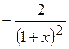 )
)
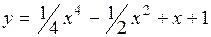 .
(Ответ:
.
(Ответ:  )
)
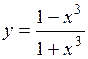 .
(Ответ:
.
(Ответ: 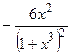 )
)
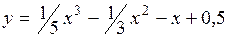 .
(Ответ:
.
(Ответ: 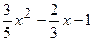 )
)
 .
(Ответ:
.
(Ответ:  )
)
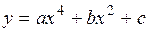 .
(Ответ: 4
.
(Ответ: 4 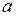
 )
)
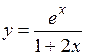 .
(Ответ:
.
(Ответ: 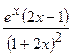 )
)
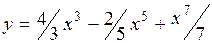 .
(Ответ:
.
(Ответ: 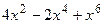 )
)
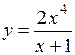 .
(Ответ:
.
(Ответ: 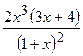 )
)
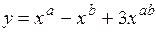 .
(Ответ:
.
(Ответ: 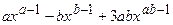 )
)
 .
(Ответ:
.
(Ответ: 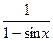 )
)
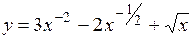 .
(Ответ:
.
(Ответ: 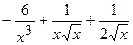 )
)
 (Ответ:
(Ответ: 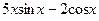 )
)
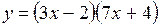 .
(Ответ:
.
(Ответ: 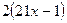 )
)
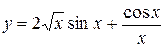 .
(
.
(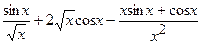 )
)
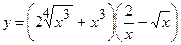 .
(
.
(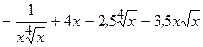 )
)
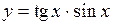 .
(Ответ:
.
(Ответ: 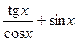 )
)
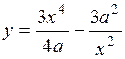 .
(Ответ:
.
(Ответ: 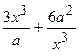 )
)
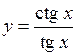 .
(Ответ: -
.
(Ответ: - 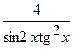 )
)
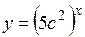 .
(Ответ:
.
(Ответ: 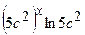 )
)
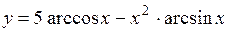 (Ответ:
(Ответ: 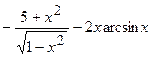 )
)
 .
(Ответ:
.
(Ответ: 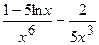 )
)
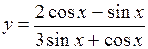 .
(Ответ: -
.
(Ответ: -  )
)
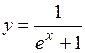 .
(Ответ:
.
(Ответ:  )
)
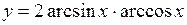 .
(Ответ:
.
(Ответ: 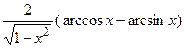 )
)
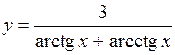 .
(Ответ: 0)
.
(Ответ: 0)
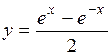 .
(Ответ:
.
(Ответ: 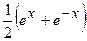 )
)
 .
(Ответ:
.
(Ответ: 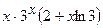 )
)
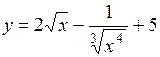 (Ответ:
(Ответ: 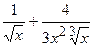 )
)
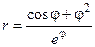 .
(Ответ:
.
(Ответ: 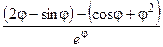 )
)
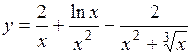 .
(Ответ:
.
(Ответ: 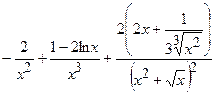
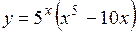 .
(Ответ:
.
(Ответ: 
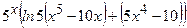 )
)
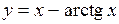 (Ответ:
(Ответ: 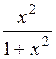 )
)
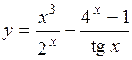 .
.
 )
)
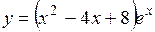 .
(Ответ:
.
(Ответ:  )
)
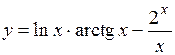 .
(Ответ:
.
(Ответ: 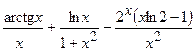 )
)
 .
(Ответ:
.
(Ответ: 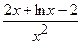 )
)
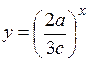 .
(Ответ:
.
(Ответ: 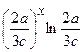 )
)
 .
(Ответ:
.
(Ответ: 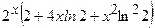 )
)
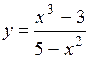 .
(Ответ:
.
(Ответ: 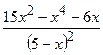 )
)
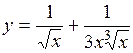 .
(Ответ:
.
(Ответ: 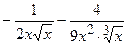 )
)
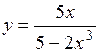 .
(Ответ:
.
(Ответ: 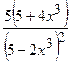 )
)
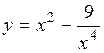 .
(Ответ:
.
(Ответ: 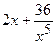 )
)
 .
(Ответ:
.
(Ответ:  )
)
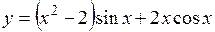 .
(Ответ:
.
(Ответ: 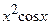 )
)
 .
(Ответ:
.
(Ответ: 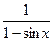 )
)
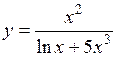 .
(Ответ:
.
(Ответ: 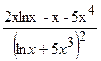 )
)
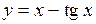 .
(Ответ:
.
(Ответ: 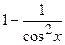 )
)
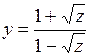 .
(Ответ:
.
(Ответ: 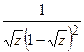 )
)
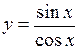 .
(Ответ:
.
(Ответ:  )
)
 .
(Ответ:
.
(Ответ: 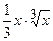 )
)
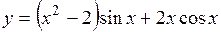 (Ответ:
(Ответ:  )
)
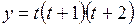 .
(Ответ:
.
(Ответ: 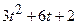 )
)
 .
(Ответ:
.
(Ответ:  )
)
 .
(Ответ:
.
(Ответ: 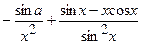 )
)
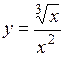 .
(Ответ:
.
(Ответ: 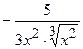 )
)
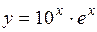 .
(Ответ:
.
(Ответ: 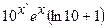 )
)
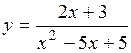 .
(Ответ:
.
(Ответ: 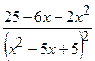 )
)
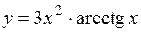 .
(Ответ:
.
(Ответ: 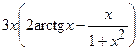 )
)
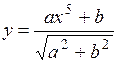 .
(Ответ:
.
(Ответ:  )
)
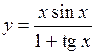 (Ответ:
(Ответ: 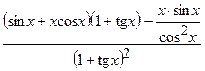 )
)
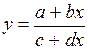 .
(Ответ:
.
(Ответ:  )
)
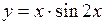 (Ответ:
(Ответ:  )
)
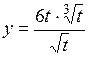 .
(Ответ:
.
(Ответ: 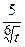 )
)
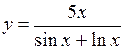 (Ответ:
(Ответ: 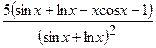 )
)
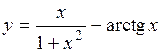 .
(Ответ:
.
(Ответ:  )
)
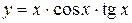 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ: 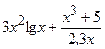 )
)
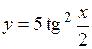 (Ответ:
(Ответ: 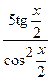 )
)
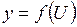 и
и 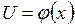 - дифференцируемые функции. Тогда сложная функция
- дифференцируемые функции. Тогда сложная функция 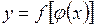 есть также дифференцируемая функция, причем
есть также дифференцируемая функция, причем .
.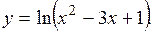
 , где
, где 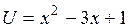 .
.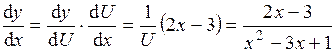 .
.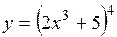 .
.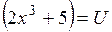 . Тогда
. Тогда  .
.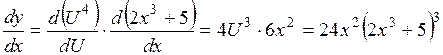 .
.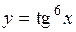 .
.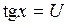 . Тогда
. Тогда 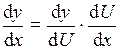 =
= 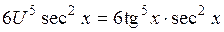 .
. .
.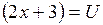 . Тогда
. Тогда 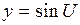 .
.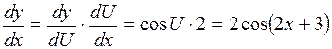 .
.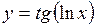 .
.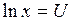 , то
, то 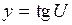 . Следовательно
. Следовательно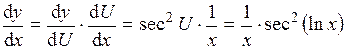 .
.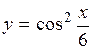 .
.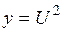 , где
, где 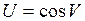 , а
, а 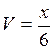 .
. =
= 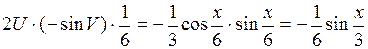 .
.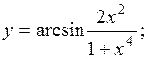
 <1.
<1.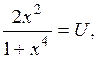 то
то 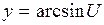 , следовательно,
, следовательно,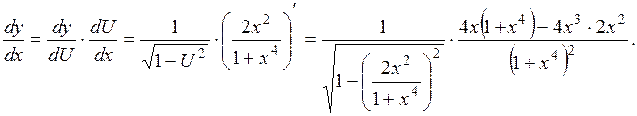 Выполним алгебраические преобразования и получим окончательно
Выполним алгебраические преобразования и получим окончательно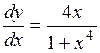 .
.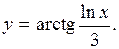

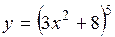 (Ответ:
(Ответ: 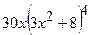 )
)
 (Ответ:
(Ответ: 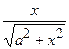 )
)
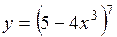 (Ответ:
(Ответ: 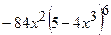 )
)
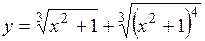 (Ответ:
(Ответ:  )
)
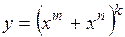 (Ответ:
(Ответ: 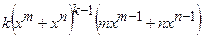 )
)
 (Ответ:
(Ответ: 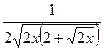 )
)
 (Ответ:
(Ответ:  )
)
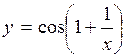 (Ответ:
(Ответ: 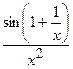 )
)
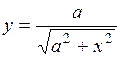 (Ответ:
(Ответ: 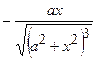 )
)
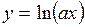 (Ответ:
(Ответ: 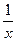 )
)
 (Ответ:
(Ответ: 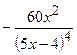 )
)
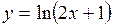 (Ответ:
(Ответ: 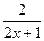 )
)
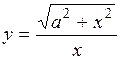 (Ответ:
(Ответ:  )
)
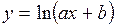 (Ответ:
(Ответ: 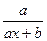 )
)
 (Ответ:
(Ответ: 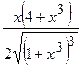 )
)
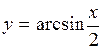
 (Ответ:
(Ответ: 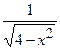 )
)
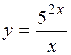 (Ответ:
(Ответ: 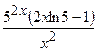 )
)
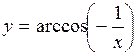 (Ответ:
(Ответ: 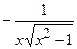 )
)
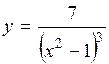 (Ответ:
(Ответ:  )
)
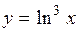 (Ответ:
(Ответ: 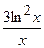 )
)
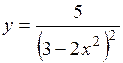 (Ответ:
(Ответ: 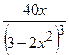 )
)
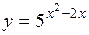 (Ответ:
(Ответ: 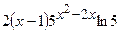 )
)
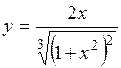 (Ответ:
(Ответ: 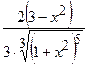 )
)
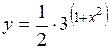 (Ответ:
(Ответ: 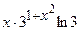 )
)
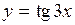 (Ответ:
(Ответ: 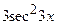 )
)
 (Ответ:
(Ответ: 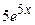 )
)
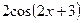 )
)
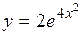 (Ответ:
(Ответ: 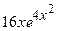 )
)
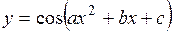 (Ответ:
(Ответ: 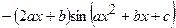 )
)
 (Ответ:
(Ответ:  )
)
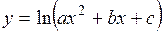 (Ответ:
(Ответ: 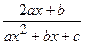 )
)
 (Ответ:
(Ответ: 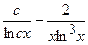 )
)
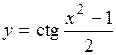 (Ответ:
(Ответ: 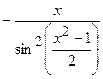 )
)
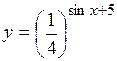 (Ответ:
(Ответ: 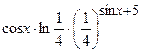 )
)
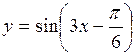 (Ответ:
(Ответ: 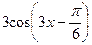 )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ: 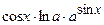 )
)
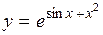 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ: 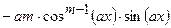 )
)
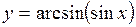 (Ответ:
(Ответ:  )
)
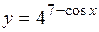 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ:  )
)
 (Ответ:
(Ответ: 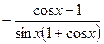 )
)
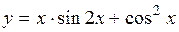 (Ответ:
(Ответ:  )
)
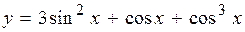 (Ответ:
(Ответ: 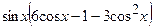 )
)
 .
.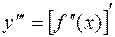
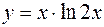 .
.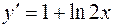 . Дифференцируя производную
. Дифференцируя производную 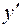 , найдем:
, найдем: 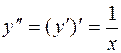 . Отсюда третья производная
. Отсюда третья производная 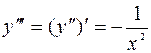 .
.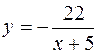 (Ответ:
(Ответ: 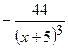 )
)
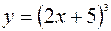 (Ответ:
(Ответ: 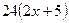 )
)
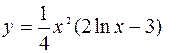 (Ответ:
(Ответ: 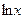 )
)
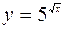 (Ответ:
(Ответ: 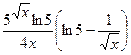 )
)
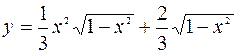 (Ответ:
(Ответ: 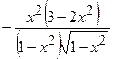 )
)
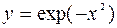 (Ответ:
(Ответ: 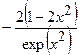 )
)
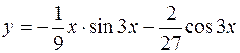 (Ответ:
(Ответ: 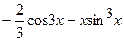 )
)
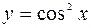 (Ответ:
(Ответ: 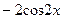 )
)
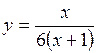 (Ответ:
(Ответ: 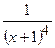 )
)
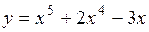 (Ответ:
(Ответ: 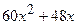 )
)
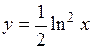 (Ответ:
(Ответ:  )
)
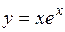 (Ответ:
(Ответ: 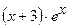 )
)
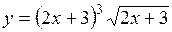 (Ответ:
(Ответ: 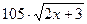 )
)
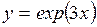 (Ответ:
(Ответ: 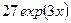 )
)
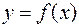 называется главная часть ее приращения, линейная относительно приращения аргумента.
называется главная часть ее приращения, линейная относительно приращения аргумента.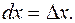
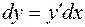
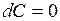 , где С=const
, где С=const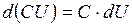
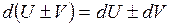
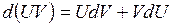
 ,
, 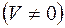

 мало по абсолютной величине, то
мало по абсолютной величине, то 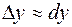 и
и 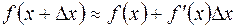 . Полученное выражение позволяет использовать дифференциал функции для приближенных вычислений.
. Полученное выражение позволяет использовать дифференциал функции для приближенных вычислений.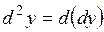 . Аналогично определяется дифференциал третьего и более высоких порядков.
. Аналогично определяется дифференциал третьего и более высоких порядков. и дифференциал
и дифференциал 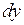 функции
функции 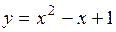 при
при  и
и 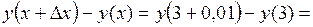
 .
. .
.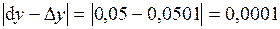 .
. .
.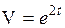 .
.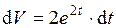 - дифференциал первого порядка,
- дифференциал первого порядка,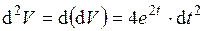 - дифференциал второго порядка.
- дифференциал второго порядка.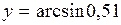 .
.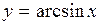 . Полагая
. Полагая  ,
, 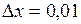 и применяя формулу
и применяя формулу 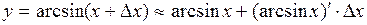 , получаем
, получаем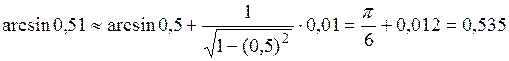 .
. . Полагая R =3,
. Полагая R =3, 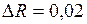 , имеем
, имеем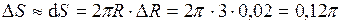 .
. .
.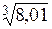 .
. и положим x=8,
и положим x=8, 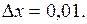
 ,
, .
.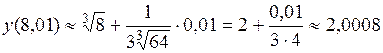 .
.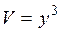 . Задача сводится к отысканию приращения
. Задача сводится к отысканию приращения  при
при  и
и 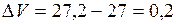 .
.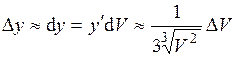 . Подставляем соответствующие значения и получаем
. Подставляем соответствующие значения и получаем (м).
(м). (Ответ:
(Ответ: 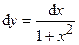 )
)
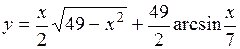 (Ответ:
(Ответ: 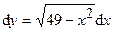 )
)
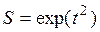 (Ответ:
(Ответ: 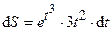 )
)
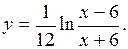 (Ответ
(Ответ  )
)
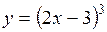 Ответ:
Ответ: 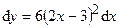 ;
;  ;
;  .
.
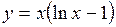 Ответ:
Ответ: 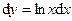 ;
; 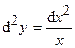 ;
; 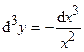 .
.
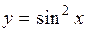 Ответ:
Ответ: 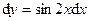 ;
; 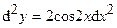 ;
; 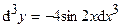 .
.
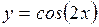 Ответ:
Ответ:  ;
;  ;
; 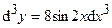 .
.
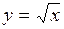 при
при 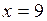 и
и 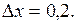 Вычислить абсолютную и относительную погрешности, которые получаются при замене функции ее дифференциалом. (Ответ:
Вычислить абсолютную и относительную погрешности, которые получаются при замене функции ее дифференциалом. (Ответ: 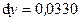 ;
;  ;
; 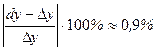 ).
). для функции
для функции 


