
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая обработка данных измерения роста.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В работе статистически обрабатываются данные измерения роста определенной группы населения. Необходимо построить гистограмму, вычислить среднее арифметическое 1. Взять результаты измерений роста[5] 100 человек, сведенные в вариационный ряд (см. приложение) и перенести их в таблицу 1.(100 измерений взято для удобства расчетов). Вычислить и занести в таблицу произведения
Таблица 1
2. Рассчитать среднее арифметическое роста 3. Составить интервальный вариационный ряд. Для этого найти приблизительную ширину интервала по формуле:
где
Например, если вариационный ряд начинается так:
то при ширине интервала 2см границы интервалов будут следующие:
Таблица 2.
4. Рассчитать и занести в таблицу 2 следующие величины: а) значения середины каждого интервала В нашем примере они имеют следующие значения:
б) суммарную частоту вариант в интервале В нашем примере эти величины имеют следующие значения в) значения г) сумму произведений 5. Рассчитать дисперсию по формуле 6. Рассчитать среднее квадратичное отклонение 7. Рассчитать среднюю ошибку среднего арифметического (округлить до одной значащей цифры). 8. Результат записать в следующем виде:
9. Построить гистограмму, являющуюся графическим изображением интервального вариационного ряда (см. табл. 2). С этой целью по оси абсцисс отложить отрезки, соответствующие интервалам. По оси ординат отложить отрезки, равные суммарным частотам вариант в интервалах 10. Оценить достоверность различий средних арифметических двух выборок. Для этого вычислить критерий достоверности по формуле
где 11. Определить интервал роста. Значение варианты xi,попадающие в интервал в интервал в интервал в интервал в интервал Руководствуясь этим, оцените величину своего роста по результатам статистической обработки роста соответствующей группы населения.
2. Провести статистический анализ для следующих совокупностей данных: 2.1. Измерено значение пульса у 25 студентов: 69, 71, 83, 66, 79, 74, 74, 79, 66, 71, 71, 74, 74, 83, 74, 79, 71, 74, 83, 74, 79, 74, 87, 79, 69. Рассчитать среднее значение пульса, дисперсию, средне квадратичное отклонение, среднюю ошибку среднего арифметического. Правильно записать результат. Построить гистограмму. Сделать вывод о характере распределения. Доверительную вероятность принять равной 0,95. 2.2. Измерен диаметр эритроцитов у кролика (размер дан в микрометрах):6,0; 5,6; 5,6; 6,8; 7,4; 6,0; 7,9; 7,4; 6,3; 6,3; 6,8; 7,2; 6,0; 6,3; 6,3; 7,4; 7,2; 6,8; 6,3; 7,2; 6,8; 6,3; 6,8; 7,2; 6,3. Рассчитать среднее значение диаметра эритроцита, дисперсию, средне квадратичное отклонение, среднюю ошибку среднего арифметического. Правильно записать результат. Построить гистограмму. Сделать вывод о характере распределения. Доверительную вероятность принять равной 0,95. 2.3. Проведены измерения систолического давления у мужчины в начальной стадии травматического шока (давление измерено в мм.рт.ст.): 140, 134, 158, 152, 140, 146, 152, 158, 122, 134, 140, 152, 148, 146, 158, 146, 134, 122, 140, 152, 148, 140, 146, 152, 146. Рассчитать среднее значение систолического давления, дисперсию, средне квадратичное отклонение, среднюю ошибку среднего арифметического. Правильно записать результат. Построить гистограмму. Сделать вывод о характере распределения. Доверительную вероятность принять равной 0,95. 2.4. Проведены измерения диастолического давления у женщин (диагноз: дистония) (давление измерено в мм.рт.ст.): 62, 50, 62, 68, 59, 62, 73, 54, 62, 65, 62, 59, 54, 62, 68, 62, 59, 65, 68, 59, 62, 59, 62, 68, 54. Рассчитать среднее значение диастолического давления, дисперсию, средне квадратичное отклонение, среднюю ошибку среднего арифметического. Правильно записать результат. Построить гистограмму. Сделать вывод о характере распределения. Доверительную вероятность принять равной 0,95. 2.5. Изучался рост (см) мужчин возраста 25 лет для сельской местности. По случайной выборке объема: 175, 167, 168, 169, 168, 170, 174, 173, 177, 172, 174, 167, 173, 172, 171, 171, 170, 167, 174, 177, 171, 172, 173, 169, 171, 173, 173, 168, 173, 172, 166, 164, 168, 172, 174. Рассчитать среднее значение роста, дисперсию, средне квадратичное отклонение, среднюю ошибку среднего арифметического. Правильно записать результат. Построить гистограмму. Сделать вывод о характере распределения. Доверительную вероятность принять равной 0,95.
ПРИЛОЖЕНИЕ. П.1. Правила приближенных вычислений. П.1.1. Запись приближенных чисел. Результат измерений представляет собой приближенное число, точность которого определяется ошибкой. Условимся записывать приближенные числа так, чтобы ошибка последней цифры не превышала десяти единиц соответствующего разряда. При такой записи все цифры числа, кроме последней, будут верными. Последняя цифра называется сомнительной, все цифры правее сомнительной – неверными. При записи окончательного результата все неверные цифры отбрасываются с соблюдением правил округления. Если приближенное число входит в расчетную формулу, в нем сохраняют одну неверную цифру, запасную. Например, если результат измерения равен 1,2763, а ошибка – 0,02, то окончательный результат – 1,28±0,02 (отброшены две неверные цифры, оставлены две верные и одна сомнительная), если же результат измерения входит в вычисления, то используется число 1,276, где цифра 6 – запасная. В таблицах математических и физических величин приводятся числа только с верными цифрами и одной сомнительной, за максимальную (т.е. предельную) ошибку округления принимается половина единицы сомнительной цифры. Пример 1. Из таблиц можно найти значение Пример 2. Из таблицы плотность ртути при 20 0С равна 19,5458·103 кг/м3. Ошибка округления равна 0,00005·103 кг/м3.
П.1.2. Правила округления Хотя правила округления считаются известными, следует напомнить, что: 1. Если первая отбрасываемая цифра больше пяти, то последняя сохраняемая цифра увеличивается на единицу, если отбрасываемая цифра меньше пяти, то последняя цифра оставляется без изменений. 2. Когда отбрасывается только цифра 5, а последующих цифр младших разрядов нет или они неизвестны, то сохраняемая четная цифра увеличивается на единицу. 3. Если округляемое число – ошибка, то при отбрасывании цифры 5 увеличиваются на единицу и четная и нечетная цифры. 4. При округлении целых чисел все цифры, отброшенные при округлении, заменяются множителем
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1533; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.153.240 (0.007 с.) |

 дисперсию D, среднее квадратичное отклонение
дисперсию D, среднее квадратичное отклонение 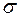 , среднюю ошибку среднего арифметического n, оценить достоверность различий средних арифметических двух выборок, рассчитав критерий достоверности (Стьюдента) t.
, среднюю ошибку среднего арифметического n, оценить достоверность различий средних арифметических двух выборок, рассчитав критерий достоверности (Стьюдента) t. для каждого значения варианты и их сумму.
для каждого значения варианты и их сумму.
 , где n -сумма частот вариант (общее число измерений), k - общее число вариант. Результат округлить до целых единиц.
, где n -сумма частот вариант (общее число измерений), k - общее число вариант. Результат округлить до целых единиц.
 разность между максимальной и минимальной вариантами; разбить вариационный ряд на интервалы с границами
разность между максимальной и минимальной вариантами; разбить вариационный ряд на интервалы с границами  Результаты занести в таблицу 2. Для того, чтобы значение варианты – границы не попало в оба соседних интервала, в данный интервал включить значение левой границы
Результаты занести в таблицу 2. Для того, чтобы значение варианты – границы не попало в оба соседних интервала, в данный интервал включить значение левой границы  а значение правой
а значение правой  включить в следующий интервал.
включить в следующий интервал. и т.д.
и т.д.
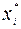
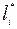




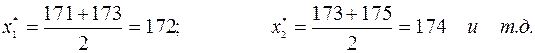
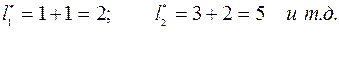
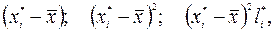

 ,где I-нумерация интервалов, к*- общее число интервалов.
,где I-нумерация интервалов, к*- общее число интервалов. .
.
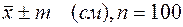 .
. Построить столбчатую диаграмму. Соединить плавной линией середины верхних сторон прямоугольников гистограммы. Полученную кривую сравнить с прямой нормального распределения и сделать вывод о характере эмпирического распределения.
Построить столбчатую диаграмму. Соединить плавной линией середины верхних сторон прямоугольников гистограммы. Полученную кривую сравнить с прямой нормального распределения и сделать вывод о характере эмпирического распределения. ,
, - средние арифметические двух разных выборок, m1,m2 –соответствующие им средние ошибки.
- средние арифметические двух разных выборок, m1,m2 –соответствующие им средние ошибки. , принято называть «средними» («рост данного человека средний»), попадающие
, принято называть «средними» («рост данного человека средний»), попадающие - «выше среднего»,
- «выше среднего»,
 - «ниже среднего»,
- «ниже среднего», - «большими»,
- «большими», - «малыми».
- «малыми». . Ошибка округления принимается равной 0,00005.
. Ошибка округления принимается равной 0,00005.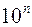 , где n – количество отброшенных цифр. При округлении десятичных дробей цифры, стоящие после запятой, просто отбрасываются, нулями их заменить нельзя, так как нуль в конце десятичной дроби характеризует точность. Например, 1,25 и 1.250 отличаются тем, что во второй дроби верных цифр три, а в первой – две. Пример округления целого числа:
, где n – количество отброшенных цифр. При округлении десятичных дробей цифры, стоящие после запятой, просто отбрасываются, нулями их заменить нельзя, так как нуль в конце десятичной дроби характеризует точность. Например, 1,25 и 1.250 отличаются тем, что во второй дроби верных цифр три, а в первой – две. Пример округления целого числа:  Пример округления дроби:
Пример округления дроби:  .
.


