Дифференциальное исчисление функций
Похожие статьи вашей тематики
СОДЕРЖАНИЕ
|
| Стр
| | Глава I.
| Пределы
|
| | Глава 2.
| Дифференциальное исчисление функций одной независимой переменной
|
| |
| §1.
| Понятие производной
|
| |
| §2.
| Основные правила дифференцирования. Дифференцирование основных элементарных функций.
|
| |
| §3.
| Дифференцирование сложной функции
|
| |
| §4.
| Производные высших порядков
|
| |
| §5.
| Дифференциал функции
|
| |
| §6.
| Применение производной при решении прикладных задач
|
| | Глава 3.
| Исследование функций методами дифференциального исчисления
|
| | §1.
| Интервалы монотонности функции
|
| |
| §2.
| Экстремум функции
|
| | Глава 4.
| Неопределенный интеграл
|
| |
| §1.
| Непосредственное интегрирование
|
| |
| §2.
| Интегрирование способом подстановки
(методом замены переменной)
|
| |
| §3.
| Интегрирование по частям
|
| |
| §4.
| Применение неопределенного интеграла при решении прикладных задач
|
| | Глава 5.
| Определенный интеграл
|
| |
| §1.
| Определенный интеграл и его непосредственное интегрирование
|
| |
| §2.
| Приложение определенного интеграла для вычисления площадей плоских фигур
|
| |
| §3.
| Приложение определенного интеграла к решению физических задач.
|
| | Глава 6.
| Дифференциальные уравнения
|
| |
| §1.
| Основные понятия
|
| |
| §2.
| Уравнения с разделяющимися переменными
|
| |
| §3.
| Однородные дифференциальные уравнения
|
| |
| §4.
| Задачи на составление дифференциальных уравнений
|
| | Глава 7.
| Элементы теории вероятностей и математической статистики
|
| |
| §1.
| Основные понятия
|
| |
| §2.
| Числовые характеристики распределения случайных величин
|
| |
| §3.
| Нормальный закон распределения случайных величин
|
| |
| §4.
| Генеральная совокупность. Оценка параметров генеральной совокупности по ее выборке
|
| |
| §5.
| Интервальная оценка. Интервальная оценка при малой выборке. Распределение Стьюдента
|
| |
| §6.
| Проверка гипотез. Критерии значимости.
|
| |
| §7.
| Элементы корреляционного и регрессионного анализа.
|
| |
|
| 7.1. Характер взаимосвязи между признаками
|
| |
|
| 7.2. Проведение корреляционного анализа с помощью коэффициента парной корреляции
|
| |
|
| 7.3. Элементы регрессионного анализа
|
| | Лабораторные работы по статистической обработке результатов
|
| |
| 1.
| Статистическая обработка данных измерения роста
|
| |
| 2.
| Задания для проведения статистического анализа совокупности данных
|
| | Приложение.
|
|
| |
| П1.
| Правила приближенных вычислений
|
| |
| П1.1
| Запись приближенных чисел
|
| |
| П1.2.
| Правила округления
|
| |
| П1.3.
| Вычисление с приближенными числами
|
| | Ответы.
|
|
| | Список литература
|
| | | | | | |
«Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой»
Леонардо да Винчи,
G.36v (Записная книжка, 186 страница)
Глава 1
ПРЕДЕЛЫ
Постоянная 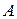 является пределом функции является пределом функции  в точке в точке  , если их разность во всех точках, кроме , если их разность во всех точках, кроме  , по абсолютному значению остается меньше бесконечно малого положительного числа e. , по абсолютному значению остается меньше бесконечно малого положительного числа e.
Если для  <e, то <e, то  . .
Практическое вычисление пределов основывается на следующих теоремах:
Если существуют  и и  то то
¯   ± ± 
¯ 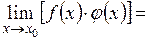  × × 
¯  (при (при  ≠0). ≠0).
Используют также следующие пределы:
 - первый замечательный предел - первый замечательный предел
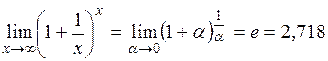 - второй замечательный предел. - второй замечательный предел.
Иногда в процессе отыскания предела при замене аргумента определенным значением функция получает выражение  или или  - неопределенность. Хотя это выражение не имеет определенного смысла, функция может иметь конечный предел при данном стремлении аргумента. Это становится очевидным, если функцию преобразовать: разложить ее на множители, или поделить на аргумент, или умножить на сопряженное выражение, и т.д. - неопределенность. Хотя это выражение не имеет определенного смысла, функция может иметь конечный предел при данном стремлении аргумента. Это становится очевидным, если функцию преобразовать: разложить ее на множители, или поделить на аргумент, или умножить на сопряженное выражение, и т.д.
Например:
ü  при замене при замене  преобразовывается в неопределенность преобразовывается в неопределенность  . .
Раскрыть неопределенность можно, поделив все члены выражения, стоящего под знаком предела, на высшую степень аргумента, то есть на  : :
 = =  . .
ü  - неопределенность. - неопределенность.
Раскрыть данную неопределенность можно, разложив выражения, стоящие в числителе и знаменателе под знаком предела, на множители, то есть:
  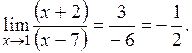
ü  - неопределенность. - неопределенность.
Умножив и поделив выражение, стоящее под знаком предела, на сопряженное выражение 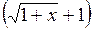 , получаем следующее выражение: , получаем следующее выражение:
 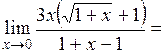
= 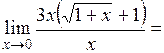  . .
Найти следующие пределы:
1.1.  .
(Ответ: 3) .
(Ответ: 3)
| 1.6.  . (Ответ: 9/2) . (Ответ: 9/2)
| 1.2.  .
(Ответ: 1000) .
(Ответ: 1000)
| 1.7.  . (Ответ: 1/3) . (Ответ: 1/3)
| 1.3.  .
(Ответ: - .
(Ответ: -  ) )
| 1.8.  . (Ответ: . (Ответ: 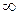 ) )
| 1.4.  . (Ответ: . (Ответ:  ) )
| 1.9.  . (Ответ: 1) . (Ответ: 1)
| 1.5.  . (Ответ: 0) . (Ответ: 0)
| 1.10.  . (Ответ: 4) . (Ответ: 4)
| 1.11.  . (Ответ: 0) . (Ответ: 0)
| 1.21.  . (Ответ: 1/2) . (Ответ: 1/2)
| 1.12.  . (Ответ: 0) . (Ответ: 0)
| 1.22 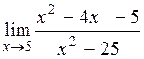 . (Ответ: 0,6) . (Ответ: 0,6)
| 1.13.  . (Ответ: 1/3) . (Ответ: 1/3)
| 1.23.  . (Ответ: 4) . (Ответ: 4)
| 1.14.  . (Ответ: 1/2) . (Ответ: 1/2)
| 1.24.  . (Ответ: 0) . (Ответ: 0)
| 1.15.  . (Ответ: 0) . (Ответ: 0)
| 1.25.  . (Ответ: 4) . (Ответ: 4)
| 1.16.  . (Ответ: 1/4) . (Ответ: 1/4)
| 1.26.  . (Ответ: e=2,718) . (Ответ: e=2,718)
| 1.17.  . (Ответ: . (Ответ:  ) )
| 1.27.  . (Ответ: 1) . (Ответ: 1)
| 1.18.  . (Ответ: 3) . (Ответ: 3)
| 1.28.  . (Ответ: e3) . (Ответ: e3)
| 1.19.  . (Ответ: 1) . (Ответ: 1)
| 1.29.  . (Ответ: 1/2) . (Ответ: 1/2)
| 1.20.  . (Ответ: 3) . (Ответ: 3)
| 1.30.  . (Ответ: 1/3) . (Ответ: 1/3)
|
Глава 2
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
Понятие производной
Пусть 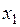 и и 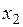 - два значения аргумента, а - два значения аргумента, а 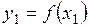 и и 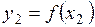 - соответствующие значения функции - соответствующие значения функции 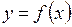 . Тогда разность . Тогда разность 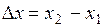 называется приращением аргумента, а разность называется приращением аргумента, а разность 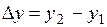 = = 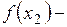 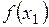 - приращением функции на отрезке - приращением функции на отрезке 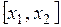 . .
Производной от функции 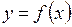 по аргументу по аргументу 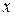 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю: называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
 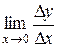
Или
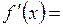 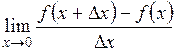
Примечание.
Производная обозначается также как 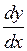 (Читается «дэ игрек по дэ икс».) Штрихом производная обозначается только в том случае, если она берется по (Читается «дэ игрек по дэ икс».) Штрихом производная обозначается только в том случае, если она берется по 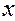 . .
Отыскание производной называется дифференцированием функции.
Исходя из определения производной, можно найти производную любой дифференцируемой функции.
Рассмотрим несколько примеров.
1. Найти производную функции
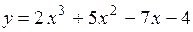 (1) (1)
Дадим 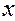 приращение приращение  , тогда , тогда  получит приращение получит приращение 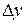 : :
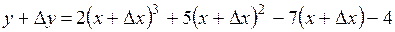 , ,
отсюда
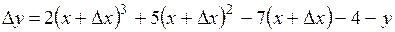 . .
Функция  задается формулой (1). Тогда задается формулой (1). Тогда
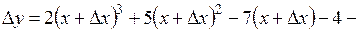 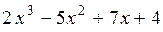 = =
= 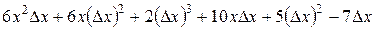
Находим отношение приращения функции к приращению аргумента:
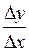 = = 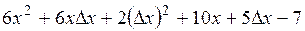 . .
Найдем предел этого отношения при 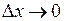 : :
 = = 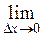 ( (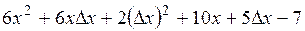 )= )= 
Следовательно, по определению производной
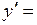 
2. Найти производную функции
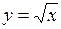 (2) (2)
Находим приращение функции 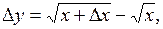 отсюда отсюда
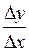 = = 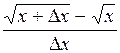 и и
 = = 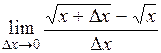
Таким образом,
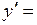 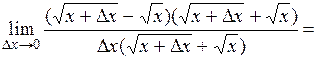  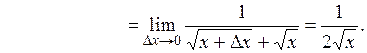
Итак,

3. Найти производную функции
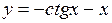 (3) (3)
Находим приращение функции

Воспользуемся формулой
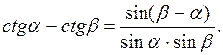
Отсюда
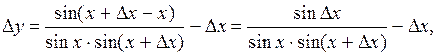
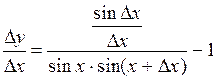
и
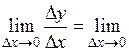  = = 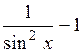 . .
Итак,
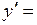 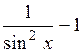 = = 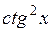
Исходя из определения производной, найти производные следующих функций:
2.1. 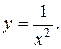 (Ответ: - (Ответ: - 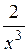 ) )
| 2.5. 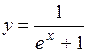 (Ответ: (Ответ: 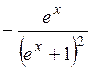 ) )
| 2.2. 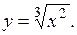 (Ответ: (Ответ: 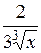 ) )
| 2.6. 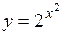 . (Ответ: . (Ответ:  ) )
| 2.3. 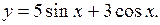 (Ответ:
(Ответ:  ) )
| 2.7.  .
(Ответ: .
(Ответ: 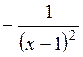 ) )
| 2.4. 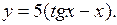 Ответ:
Ответ:  ) )
| 2.8.  .
(Ответ: 6(x-1)) .
(Ответ: 6(x-1))
|
Производные высших порядков
Производная второго порядка (вторая производная) от функции 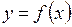 есть производная от ее производной, т.е. есть производная от ее производной, т.е.
 . .
Производная третьего порядка (третья производная) от функции 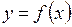 есть производная от ее второй производной: есть производная от ее второй производной:
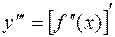
Вообще производная n-го порядка (n-я производная) функции 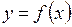 есть производная от ее (n-1)-й производной. есть производная от ее (n-1)-й производной.
Рассмотрим пример.
Найти третью производную от функции 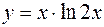 . .
Дифференцируя данную функцию, получим 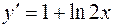 . Дифференцируя производную . Дифференцируя производную 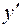 , найдем: , найдем: 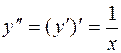 . Отсюда третья производная . Отсюда третья производная 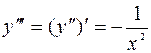 . .
Найти производные второго порядка от функций:
| 2.127.
| 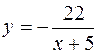 (Ответ:
(Ответ: 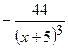 ) )
| 2.128
| 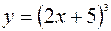 (Ответ:
(Ответ: 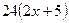 ) )
| | 2.129.
| 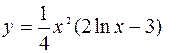 (Ответ:
(Ответ: 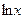 ) )
| 2.130.
| 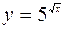 (Ответ:
(Ответ: 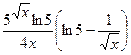 ) )
| | 2.131.
| 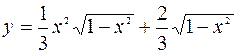 (Ответ:
(Ответ: 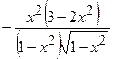 ) )
| 2.132.
| 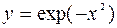 (Ответ:
(Ответ: 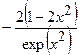 ) )
| | 2.133.
| 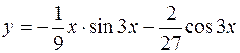 (Ответ:
(Ответ: 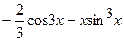 ) )
| 2.134
| 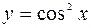 (Ответ:
(Ответ: 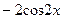 ) )
| | | | | | |
Найти производные третьего порядка от функций:
| 2.135.
| 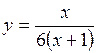 (Ответ:
(Ответ: 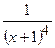 ) )
| 2.136.
| 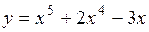 (Ответ:
(Ответ: 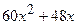 ) )
| | 2.137.
| 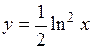 (Ответ:
(Ответ:  ) )
| 2.138.
| 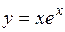 (Ответ:
(Ответ: 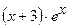 ) )
| | 2.139.
| 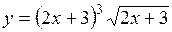 (Ответ:
(Ответ: 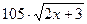 ) )
| 2.140.
| 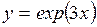 (Ответ:
(Ответ: 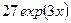 ) )
|
Дифференциал функции
Дифференциалом (первого порядка) функции 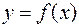 называется главная часть ее приращения, линейная относительно приращения аргумента. называется главная часть ее приращения, линейная относительно приращения аргумента.
Дифференциалом аргумента называется приращение этого аргумента: 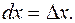
Дифференциал функции равен произведению ее производной на дифференциал аргумента:
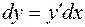
Основные свойства дифференциала.
1. 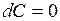 , где С=const , где С=const
2. 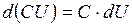
3. 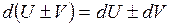
4. 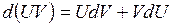
5.  , , 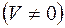
6. 
Если приращение аргумента  мало по абсолютной величине, то мало по абсолютной величине, то 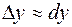 и и 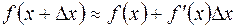 . Полученное выражение позволяет использовать дифференциал функции для приближенных вычислений. . Полученное выражение позволяет использовать дифференциал функции для приближенных вычислений.
Дифференциалом второго порядка функции 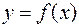 называется дифференциал от дифференциала первого порядка: называется дифференциал от дифференциала первого порядка: 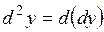 . Аналогично определяется дифференциал третьего и более высоких порядков. . Аналогично определяется дифференциал третьего и более высоких порядков.
Используя определение дифференциала, рассмотрим ряд примеров.
1. Найти приращение  и дифференциал и дифференциал 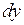 функции функции 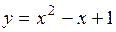 при при  и и  =0,01. Каковы абсолютная и относительная погрешности, которые допускаются при замене приращения функции ее дифференциалом? =0,01. Каковы абсолютная и относительная погрешности, которые допускаются при замене приращения функции ее дифференциалом?
Имеем
 = = 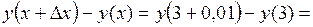  . .
Найдем дифференциал функции:
 . .
Абсолютная погрешность
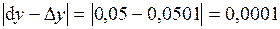 . .
Относительная погрешность
 . .
2. Найти дифференциалы первого и второго порядков функции 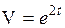 . .
Имеем
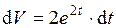 - дифференциал первого порядка, - дифференциал первого порядка,
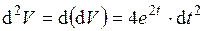 - дифференциал второго порядка. - дифференциал второго порядка.
3. Вычислить приближенное значение 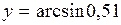 . .
Рассмотрим функцию 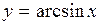 . Полагая . Полагая  , , 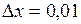 и применяя формулу и применяя формулу 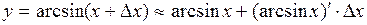 , получаем , получаем
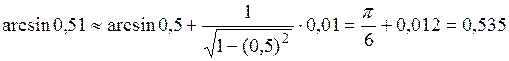 . .
4. Вычислить приближенное значение площади круга, радиус которого равен 3,02 м.
Воспользуемся формулой  . Полагая R =3, . Полагая R =3, 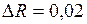 , имеем , имеем
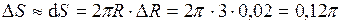 . .
Следовательно, площадь круга радиуса 3,02м имеет приближенное значение
 . .
5. Вычислить приближенно 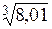 . .
Рассмотрим функцию  и положим x=8, и положим x=8, 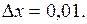
Тогда, воспользовавшись формулой  , ,
найдем
 . .
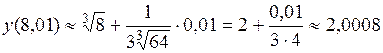 . .
Таким образом, 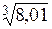 »2,0008. »2,0008.
6. На сколько увеличилось ребро куба, если объем его изменился с 27 м3 до 27,2 м3?
Если  - ребро куба, то его объем - ребро куба, то его объем 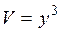 . Задача сводится к отысканию приращения . Задача сводится к отысканию приращения  функции функции  при при  и и 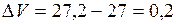 . .
Приращение  найдем, исходя из приближенного равенства найдем, исходя из приближенного равенства
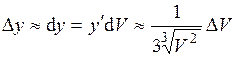 . Подставляем соответствующие значения и получаем . Подставляем соответствующие значения и получаем
 (м). (м).
Найти дифференциалы следующих функций:
| 2.141.
|  (Ответ:
(Ответ: 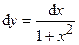 ) )
| 2.142.
| 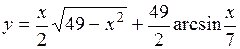 (Ответ:
(Ответ: 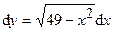 ) )
| | 2.143
| 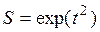 (Ответ:
(Ответ: 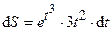 ) )
| 2.144.
| 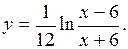 (Ответ
(Ответ  ) )
| Найти дифференциалы первого, второго и третьего порядков.
| 2.145.
| 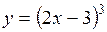 Ответ:
Ответ: 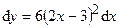 ; ;  ; ;  . .
| | 2.146.
| 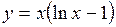 Ответ:
Ответ: 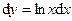 ; ; 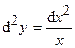 ; ; 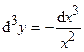 . .
| | 2.147.
| 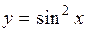 Ответ:
Ответ: 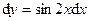 ; ; 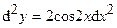 ; ; 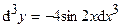 . .
| | 2.148.
| 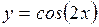 Ответ:
Ответ:  ; ;  ; ; 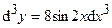 . .
|
2.149. Найти приращение и дифференциал функции 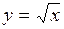 при при 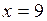 и и 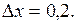 Вычислить абсолютную и относительную погрешности, которые получаются при замене функции ее дифференциалом. (Ответ: Вычислить абсолютную и относительную погрешности, которые получаются при замене функции ее дифференциалом. (Ответ: 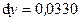 ; ;  ; ; 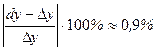 ). ).
2.150. Вычислить  и и  для функции для функции  при при  и и 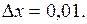 (Ответ: (Ответ:  ; ; 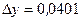 ). ).
2.151. Найти приращение и дифференциал функции  при при  и и 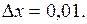 Вычислить абсолютную и относительную погрешности, которые получаются при замене функции ее дифференциалом. Вычислить абсолютную и относительную погрешности, которые получаются при замене функции ее дифференциалом.
(Ответ:  ; ; 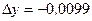 ; ;  ; ;  ). ).
2.152. На сколько измениться сторона квадрата, если его площадь уменьшится с 16 м2 до 15,82 м2? (Ответ:0,0225 м)
2.153. Найти приближенное значение объема шара радиусом R=2,01 м. (Ответ:34,04 м3).
2.154. Найти приближенное значение  . (Ответ: . (Ответ:  ) )
2.155. Найти приближенное значение  .(Ответ:2,999) .(Ответ:2,999)
2.156. Найти приближенное значение 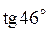 .(Ответ:1,035) .(Ответ:1,035)
2.157. Найти приближенное значение  . (Ответ:0,88) . (Ответ:0,88)
2.158. Поверхностная энергия жидкости рассчитывается по формуле:  . Здесь . Здесь  - энергия единицы площади, равная коэффициенту поверхностного натяжения, - энергия единицы площади, равная коэффициенту поверхностного натяжения,  - площадь свободной поверхности жидкости. Найти изменение поверхностной энергии мыльного пузыря при увеличении его радиуса с 5 см до 5,2 см (площадь поверхности сферы - площадь свободной поверхности жидкости. Найти изменение поверхностной энергии мыльного пузыря при увеличении его радиуса с 5 см до 5,2 см (площадь поверхности сферы  ). Коэффициент поверхностного натяжения мыльной воды в условиях данной задачи принять равным 0,04 Дж/м2 . (Ответ: ). Коэффициент поверхностного натяжения мыльной воды в условиях данной задачи принять равным 0,04 Дж/м2 . (Ответ: 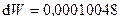 Дж). Дж).
2.159. Резиновый шар наполняется газом. Найти приближенно абсолютное и относительное изменение поверхности шара при увеличении его радиуса от 10,0 см до 10,5 см.
(Ответ:  м2; м2;  ) )
2.160. Период колебания математического маятника  , где , где  м/с2, а м/с2, а  см. Найти изменение периода колебаний при уменьшении длины на 1 см. (Ответ: см. Найти изменение периода колебаний при уменьшении длины на 1 см. (Ответ:  с) с)
2.161. Разность потенциалов между внутренней частью клетки и внешней средой обусловлена различием концентрации ионов внутри  и вне и вне  клетки. Величина этой разности потенциалов в милливольтах для одновалентных ионов при температуре 180 определяется формулой клетки. Величина этой разности потенциалов в милливольтах для одновалентных ионов при температуре 180 определяется формулой  , где , где  . .
Рассчитать изменение  при увеличении при увеличении  от 20 до 22. Учесть, что от 20 до 22. Учесть, что  . (Ответ: . (Ответ:  мВ). мВ).
Прикладных задач
Производная 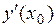 от функции от функции  , вычисленная при значении аргумента , вычисленная при значении аргумента  , представляет собой скорость изменения этой функции относительно независимой переменной , представляет собой скорость изменения этой функции относительно независимой переменной  в точке в точке  . .
В частности, если зависимость между пройденным путем  и временем и временем  при прямолинейном движении выражается формулой при прямолинейном движении выражается формулой  , то скорость движения в любой момент времени есть , то скорость движения в любой момент времени есть  , а ускорение, т.е. скорость изменения скорости движения, , а ускорение, т.е. скорость изменения скорости движения,  . .
Например.
1. Точка движется прямолинейно по закону 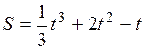 . .  выражается в метрах, а выражается в метрах, а  - в секундах. (Обратите внимание на то, что коэффициенты при соответствующих степенях - в секундах. (Обратите внимание на то, что коэффициенты при соответствующих степенях  имеют разную размерность. Не забывайте, что если слева стоят «метры», то и каждое слагаемое в правой части должно тоже иметь размерность «метры»). Найти скорость и ускорение движения через 1 с после начала движения. имеют разную размерность. Не забывайте, что если слева стоят «метры», то и каждое слагаемое в правой части должно тоже иметь размерность «метры»). Найти скорость и ускорение движения через 1 с после начала движения.
Глава 3
Решение.
Найдем производную заданной функции:  . .
При  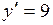 >0 - функция возрастает, >0 - функция возрастает,
при 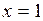  <0 - функция убывает, <0 - функция убывает,
при 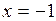 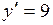 >0 - функция возрастает, >0 - функция возрастает,
при  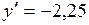 <0 - функция убывает. <0 - функция убывает.
2. Найти интервалы возрастания и убывания функции  , если , если  . .
Решение.
Найдем производную заданной функции:  . В промежутке . В промежутке  производная производная  >0 поэтому функция возрастает, а в промежутках >0 поэтому функция возрастает, а в промежутках  и и  производная производная  <0 – функция убывает. <0 – функция убывает.
3. Определить характер монотонности функции 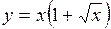 в промежутке в промежутке  . .
Решение.
Найдем производную:  . При . При 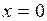 производная производная  >0 функция возрастает. При >0 функция возрастает. При 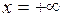 производная производная  >0 – функция возрастает. Следовательно, функция возрастает во всей области определения. >0 – функция возрастает. Следовательно, функция возрастает во всей области определения.
Решить следующие задачи.
3.1. Убедиться, что функция  в интервале в интервале  < <  <3 убывает. <3 убывает.
3.2. Определить интервалы убывания и возрастания функции  . (Ответ: при x<0 функция убывает, при x>0 - возрастает.) . (Ответ: при x<0 функция убывает, при x>0 - возрастает.)
3.3. Определить, при каких значениях  функция функция 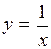 убывает. убывает.
(Ответ: при любом 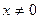 функция убывает). функция убывает).
3.4. Проверить, во всем ли интервале  функция функция  возрастает. (Ответ: при возрастает. (Ответ: при  функция убывает). функция убывает).
3.5. Определить интервал возрастания функции  . (Ответ: при x>0 функция возрастает). . (Ответ: при x>0 функция возрастает).
3.6. Найти интервалы возрастания и убывания функции  . (Ответ: в интервале . (Ответ: в интервале  и и 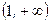 функция возрастает; в интервале функция возрастает; в интервале  - убывает). - убывает).
3.7. Найти интервалы монотонности функции  . (Ответ: интервал возрастания . (Ответ: интервал возрастания  , интервал убывания , интервал убывания 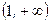 ) )
Экстремум функции
Точка  называется точкой максимума (минимума) функции называется точкой максимума (минимума) функции  , если существует такая окрестность точки , если существует такая окрестность точки  , что для всех , что для всех   этой окрестности выполняется неравенство этой окрестности выполняется неравенство  < <  (максимум) или (максимум) или  > >  (минимум). (минимум).
Точки максимума и минимума функции называются точками ее экстремума, а значение функции в точке максимума (минимума) – максимумом (минимумом), или экстремумом функции.
Правило отыскания экстремумов функции:
1. Вычислить производную  . .
2. Составить уравнение  =0 и найти его корни, которые являются критическими точками функции. =0 и найти его корни, которые являются критическими точками функции.
3. Установить знак производной  слева и справа от критической точки. слева и справа от критической точки.
Если при переходе через критическую точку производная меняет знак с плюса на минус (вторая производная при этом меньше нуля), то в критической точке она имеет максимум.
Если производная в критической точке меняет знак с минуса на плюс (вторая производная при этом больше нуля), то функция в этом точке имеет минимум.
Рассмотрим примеры.
1. Исследовать на экстремум функцию  . .
Решение.
Находим первую производную заданной функции:  . Приравниваем ее нулю и определяем критические точки: . Приравниваем ее нулю и определяем критические точки: 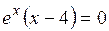 , значение , значение  является критической точкой. Определяем знак является критической точкой. Определяем знак  при переходе через критическую точку. Если при переходе через критическую точку. Если  , то , то  | 


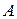 является пределом функции
является пределом функции  в точке
в точке  , если их разность во всех точках, кроме
, если их разность во всех точках, кроме  <e, то
<e, то  .
. и
и  то
то
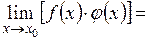
 (при
(при  - первый замечательный предел
- первый замечательный предел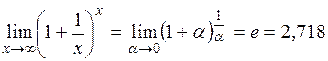 - второй замечательный предел.
- второй замечательный предел. или
или  - неопределенность. Хотя это выражение не имеет определенного смысла, функция может иметь конечный предел при данном стремлении аргумента. Это становится очевидным, если функцию преобразовать: разложить ее на множители, или поделить на аргумент, или умножить на сопряженное выражение, и т.д.
- неопределенность. Хотя это выражение не имеет определенного смысла, функция может иметь конечный предел при данном стремлении аргумента. Это становится очевидным, если функцию преобразовать: разложить ее на множители, или поделить на аргумент, или умножить на сопряженное выражение, и т.д. при замене
при замене  преобразовывается в неопределенность
преобразовывается в неопределенность  :
: .
. - неопределенность.
- неопределенность.

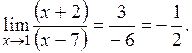
 - неопределенность.
- неопределенность.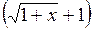 , получаем следующее выражение:
, получаем следующее выражение:
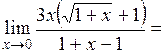
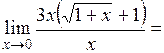
 .
. .
(Ответ: 3)
.
(Ответ: 3)
 . (Ответ: 9/2)
. (Ответ: 9/2)
 .
(Ответ: 1000)
.
(Ответ: 1000)
 . (Ответ: 1/3)
. (Ответ: 1/3)
 .
(Ответ: -
.
(Ответ: -  )
)
 . (Ответ:
. (Ответ: 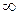 )
)
 . (Ответ:
. (Ответ:  )
)
 . (Ответ: 1)
. (Ответ: 1)
 . (Ответ: 0)
. (Ответ: 0)
 . (Ответ: 4)
. (Ответ: 4)
 . (Ответ: 0)
. (Ответ: 0)
 . (Ответ: 1/2)
. (Ответ: 1/2)
 . (Ответ: 0)
. (Ответ: 0)
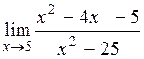 . (Ответ: 0,6)
. (Ответ: 0,6)
 . (Ответ: 1/3)
. (Ответ: 1/3)
 . (Ответ: 4)
. (Ответ: 4)
 . (Ответ: 1/2)
. (Ответ: 1/2)
 . (Ответ: 0)
. (Ответ: 0)
 . (Ответ: 0)
. (Ответ: 0)
 . (Ответ: 4)
. (Ответ: 4)
 . (Ответ: 1/4)
. (Ответ: 1/4)
 . (Ответ: e=2,718)
. (Ответ: e=2,718)
 . (Ответ:
. (Ответ:  )
)
 . (Ответ: 1)
. (Ответ: 1)
 . (Ответ: 3)
. (Ответ: 3)
 . (Ответ: e3)
. (Ответ: e3)
 . (Ответ: 1)
. (Ответ: 1)
 . (Ответ: 1/2)
. (Ответ: 1/2)
 . (Ответ: 3)
. (Ответ: 3)
 . (Ответ: 1/3)
. (Ответ: 1/3)
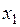 и
и 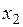 - два значения аргумента, а
- два значения аргумента, а 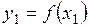 и
и 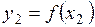 - соответствующие значения функции
- соответствующие значения функции 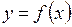 . Тогда разность
. Тогда разность 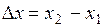 называется приращением аргумента, а разность
называется приращением аргумента, а разность 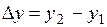 =
= 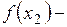
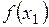 - приращением функции на отрезке
- приращением функции на отрезке 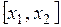 .
.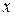 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
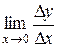
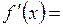
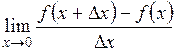
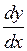 (Читается «дэ игрек по дэ икс».) Штрихом производная обозначается только в том случае, если она берется по
(Читается «дэ игрек по дэ икс».) Штрихом производная обозначается только в том случае, если она берется по 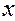 .
.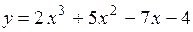 (1)
(1) , тогда
, тогда  получит приращение
получит приращение 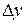 :
: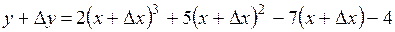 ,
,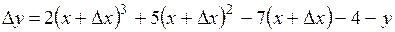 .
.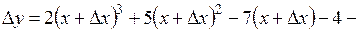
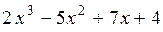 =
=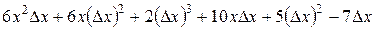
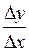 =
= 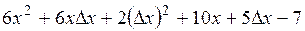 .
.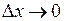 :
: =
= 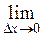 (
(
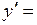
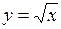 (2)
(2)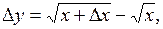 отсюда
отсюда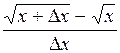 и
и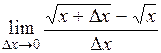
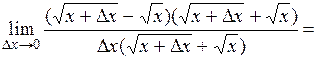

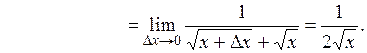

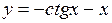 (3)
(3)
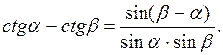
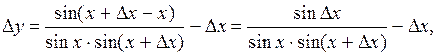
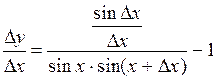
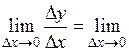
 =
= 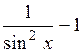 .
.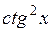
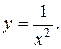 (Ответ: -
(Ответ: - 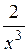 )
)
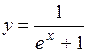 (Ответ:
(Ответ: 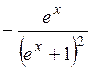 )
)
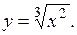 (Ответ:
(Ответ: 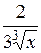 )
)
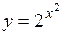 . (Ответ:
. (Ответ:  )
)
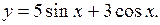 (Ответ:
(Ответ:  )
)
 .
(Ответ:
.
(Ответ: 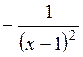 )
)
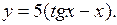 Ответ:
Ответ:  )
)
 .
(Ответ: 6(x-1))
.
(Ответ: 6(x-1))
 .
.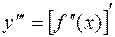
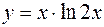 .
.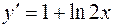 . Дифференцируя производную
. Дифференцируя производную 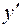 , найдем:
, найдем: 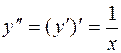 . Отсюда третья производная
. Отсюда третья производная 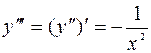 .
.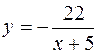 (Ответ:
(Ответ: 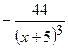 )
)
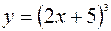 (Ответ:
(Ответ: 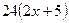 )
)
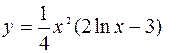 (Ответ:
(Ответ: 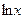 )
)
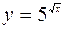 (Ответ:
(Ответ: 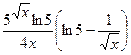 )
)
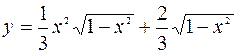 (Ответ:
(Ответ: 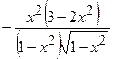 )
)
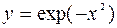 (Ответ:
(Ответ: 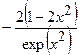 )
)
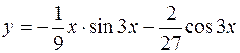 (Ответ:
(Ответ: 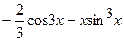 )
)
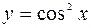 (Ответ:
(Ответ: 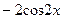 )
)
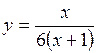 (Ответ:
(Ответ: 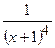 )
)
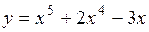 (Ответ:
(Ответ: 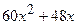 )
)
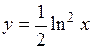 (Ответ:
(Ответ:  )
)
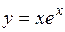 (Ответ:
(Ответ: 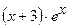 )
)
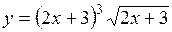 (Ответ:
(Ответ: 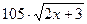 )
)
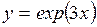 (Ответ:
(Ответ: 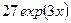 )
)
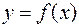 называется главная часть ее приращения, линейная относительно приращения аргумента.
называется главная часть ее приращения, линейная относительно приращения аргумента.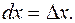
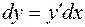
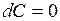 , где С=const
, где С=const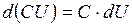
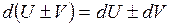
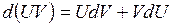
 ,
, 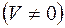

 мало по абсолютной величине, то
мало по абсолютной величине, то 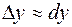 и
и 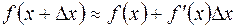 . Полученное выражение позволяет использовать дифференциал функции для приближенных вычислений.
. Полученное выражение позволяет использовать дифференциал функции для приближенных вычислений.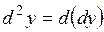 . Аналогично определяется дифференциал третьего и более высоких порядков.
. Аналогично определяется дифференциал третьего и более высоких порядков. и дифференциал
и дифференциал 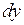 функции
функции 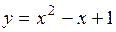 при
при  и
и 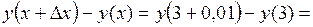
 .
. .
.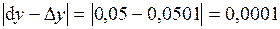 .
. .
.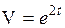 .
.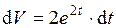 - дифференциал первого порядка,
- дифференциал первого порядка,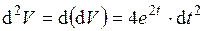 - дифференциал второго порядка.
- дифференциал второго порядка.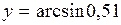 .
.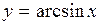 . Полагая
. Полагая  ,
, 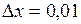 и применяя формулу
и применяя формулу 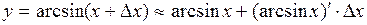 , получаем
, получаем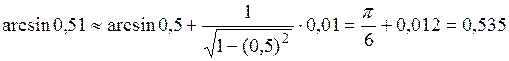 .
. . Полагая R =3,
. Полагая R =3, 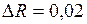 , имеем
, имеем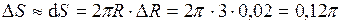 .
. .
.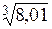 .
. и положим x=8,
и положим x=8, 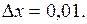
 ,
, .
.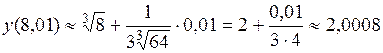 .
.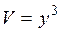 . Задача сводится к отысканию приращения
. Задача сводится к отысканию приращения  при
при  и
и 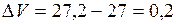 .
.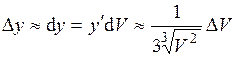 . Подставляем соответствующие значения и получаем
. Подставляем соответствующие значения и получаем (м).
(м). (Ответ:
(Ответ: 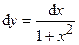 )
)
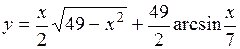 (Ответ:
(Ответ: 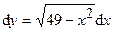 )
)
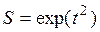 (Ответ:
(Ответ: 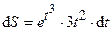 )
)
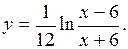 (Ответ
(Ответ  )
)
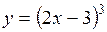 Ответ:
Ответ: 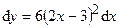 ;
;  ;
;  .
.
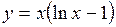 Ответ:
Ответ: 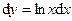 ;
; 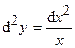 ;
; 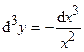 .
.
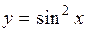 Ответ:
Ответ: 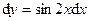 ;
; 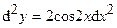 ;
; 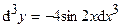 .
.
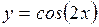 Ответ:
Ответ:  ;
;  ;
; 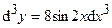 .
.
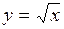 при
при 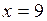 и
и 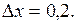 Вычислить абсолютную и относительную погрешности, которые получаются при замене функции ее дифференциалом. (Ответ:
Вычислить абсолютную и относительную погрешности, которые получаются при замене функции ее дифференциалом. (Ответ: 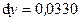 ;
;  ;
; 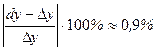 ).
). для функции
для функции  при
при  ;
; 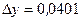 ).
). при
при  и
и  ;
; 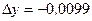 ;
;  ;
;  ).
). . (Ответ:
. (Ответ:  )
) .(Ответ:2,999)
.(Ответ:2,999)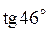 .(Ответ:1,035)
.(Ответ:1,035) . (Ответ:0,88)
. (Ответ:0,88) . Здесь
. Здесь  - энергия единицы площади, равная коэффициенту поверхностного натяжения,
- энергия единицы площади, равная коэффициенту поверхностного натяжения,  - площадь свободной поверхности жидкости. Найти изменение поверхностной энергии мыльного пузыря при увеличении его радиуса с 5 см до 5,2 см (площадь поверхности сферы
- площадь свободной поверхности жидкости. Найти изменение поверхностной энергии мыльного пузыря при увеличении его радиуса с 5 см до 5,2 см (площадь поверхности сферы  ). Коэффициент поверхностного натяжения мыльной воды в условиях данной задачи принять равным 0,04 Дж/м2 . (Ответ:
). Коэффициент поверхностного натяжения мыльной воды в условиях данной задачи принять равным 0,04 Дж/м2 . (Ответ: 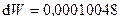 Дж).
Дж). м2;
м2;  )
) , где
, где  м/с2, а
м/с2, а  см. Найти изменение периода колебаний при уменьшении длины на 1 см. (Ответ:
см. Найти изменение периода колебаний при уменьшении длины на 1 см. (Ответ:  с)
с) и вне
и вне  клетки. Величина этой разности потенциалов в милливольтах для одновалентных ионов при температуре 180 определяется формулой
клетки. Величина этой разности потенциалов в милливольтах для одновалентных ионов при температуре 180 определяется формулой  , где
, где  .
. при увеличении
при увеличении  от 20 до 22. Учесть, что
от 20 до 22. Учесть, что  . (Ответ:
. (Ответ:  мВ).
мВ).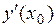 от функции
от функции  , вычисленная при значении аргумента
, вычисленная при значении аргумента  , представляет собой скорость изменения этой функции относительно независимой переменной
, представляет собой скорость изменения этой функции относительно независимой переменной  в точке
в точке  при прямолинейном движении выражается формулой
при прямолинейном движении выражается формулой  , то скорость движения в любой момент времени есть
, то скорость движения в любой момент времени есть  , а ускорение, т.е. скорость изменения скорости движения,
, а ускорение, т.е. скорость изменения скорости движения,  .
.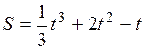 .
.  .
.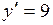 >0 - функция возрастает,
>0 - функция возрастает,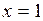
 <0 - функция убывает,
<0 - функция убывает,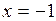
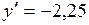 <0 - функция убывает.
<0 - функция убывает. , если
, если  .
. . В промежутке
. В промежутке  производная
производная  >0 поэтому функция возрастает, а в промежутках
>0 поэтому функция возрастает, а в промежутках  и
и  производная
производная 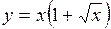 в промежутке
в промежутке  .
. . При
. При 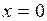 производная
производная  >0 функция возрастает. При
>0 функция возрастает. При 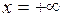 производная
производная  >0 – функция возрастает. Следовательно, функция возрастает во всей области определения.
>0 – функция возрастает. Следовательно, функция возрастает во всей области определения. в интервале
в интервале  <
<  . (Ответ: при x<0 функция убывает, при x>0 - возрастает.)
. (Ответ: при x<0 функция убывает, при x>0 - возрастает.)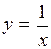 убывает.
убывает.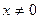 функция убывает).
функция убывает). функция
функция  возрастает. (Ответ: при
возрастает. (Ответ: при  функция убывает).
функция убывает). . (Ответ: при x>0 функция возрастает).
. (Ответ: при x>0 функция возрастает). . (Ответ: в интервале
. (Ответ: в интервале  и
и 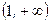 функция возрастает; в интервале
функция возрастает; в интервале  - убывает).
- убывает). . (Ответ: интервал возрастания
. (Ответ: интервал возрастания  , интервал убывания
, интервал убывания  , что для всех
, что для всех  этой окрестности выполняется неравенство
этой окрестности выполняется неравенство  <
<  (максимум) или
(максимум) или  .
. .
. . Приравниваем ее нулю и определяем критические точки:
. Приравниваем ее нулю и определяем критические точки: 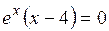 , значение
, значение  является критической точкой. Определяем знак
является критической точкой. Определяем знак 


