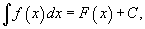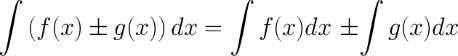Дифференциал функции.Аналитический и геометрический смысл дифференциала

Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента) и обознвчается dy

Дифференциал функции,в общем случае отличаясь от приращения функции,представляет собой главную часть этого приращения,линейную относительно приращения аргумента.В этом заключается аналитический смысл дифференциала

 

Дифференциал функции является приращением ординаты касательной(АВ), которое соответствует приращению D х (МВ) абсциссы. В этом заключается геометрический смысл дифференциала.

Дифференциалом называют приращение аргумента,т.е dx= Δx

 

Первообразная функции. Неопределенный интеграл, его свойства. Таблица основных неопределенных интегралов.

Функция F (x) называется первообразной для функции f (x) на интервале (a,b), если она дифференцируема на этом интервале и в каждой его точке

F’(x)=f(x)

Множество всех первообразных некоторой функции f (x) называется неопределенным интегралом функции f (x) и обозначается как

Функция f(x) называется подынтегральной функцией,f(x)dx- подынтегральным выражением

Если F(x)- какая-нибудь первообразная функции f(x),то

 

где С - произвольная постоянная.

Свойства неопр интеграла:

. Дифференциал от неопределенного интеграла равен подынтегральному выражению

Производная от неопределенного интеграла равна подынтегральной функции

Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная

Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла

Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций

 

 

5. Определенный интеграл. Формула Ньютона-Лейбница. Свойства определенного интеграла. Геометрический смысл определенного интеграла.
Определенный интеграл.

Разность F(b)-F(a) или значение приращения любой первообразной от данной функции f(x) при изменении аргумента от x=a до x=b называется определенным интегралом функции f(x) в пределах от а до b:

_a ∫^bf(x)dx =F(b)-F(a)

это формула Ньютона-Лейбница

 

 

Свойства определенного интеграла.
1. Определенный интеграл с равными пределами равен нулю:
_b∫^af(x) dx= 0
2. При перемене местами пределов интегрирования величина определенного интеграла изменяется на противоположную:
_a∫^bf(x) dx= - _b∫^af(x)dx
3. Если отрезок интегрирования [a,b] разделен на конечное число nчастичных отрезков [a,x₁], [x₁,x₂],…..,[x_n-1,b], то определенный интеграл от функции f(x) на отрезке [a,b]равен сумме определенных интегралов от этой функции на каждом из частичных отрезков (свойств аддитивности):
_a∫^bf(x) dx= _a ∫^x1 f(x) d x + _x1∫^x2+ ……._xn-1∫^bf(x) dx

4. _a∫^bkf (x)dx = k_a∫^bf(x) dx,
где k- постоянный множитель

5. Определенный интеграл от алгебраической суммы конечного числа функций, интегрируемых на отрезке [a,b], равен алгебраической сумме определенных интегралов этих функций на данном отрезке:
_a∫^b[f₁(x)+f₂(x)+….+f_n(x)]dx =_a∫^bf₁(x)dx+_a∫^bf₂(x)dx +….._a∫^bf_n(x)dx

Геометрический смысл определенного интеграла.
Плоская фигура, ограниченная сверху графиком непрерывной функции y=f(x), снизу –осью абцисс,
слева-прямой линиейx=a, а справа – прямой линией x=b, называется криволинейной трапецией.
Площадь криволинейной трапеции, ограниченной графиком функции y=f(x), осенью абцисс и прямыми линиями x=a и x=b, численно равна определенному интегралу от этой функции на отрезке [a,b]. В этом и заключается геометрическая интерпретация.

Понятие дифференциального уравнения. Порядок уравнения, общее и частное решение дифференциального уравнения. Дифференциальные уравнения первого порядка с разделяющимися переменными, алгоритм их решения.

Понятие дифференциального уравнения.
Уравнение, в общем случае связывающее искомую функцию y=f(x), ее аргумент x, а также производные различных порядков этой функции, называется обыкновенным дифференциальным уравнением.
F(x, y, y', y'',……,y⁽ⁿ⁾)=0

Порядок уравнения, общее и частное решение дифференциального уравнения.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в это уравнение.

Общий вид дифференциального уравнения первого порядка: F(x,y, y')=0
Общим решением дифференциального уравнения называется функция, удовлетворяющая двум условиям: во-первых, эта функция должна удовлетворять данному дифференциальному уравнению, т.е. при подстановке в уравнение должна обращать его в тождество; во-вторых, количество произвольных постоянных в этой функции должно быть равным порядку данного уравнения.

Общее решения дифференциального уравнения n-го порядка имеет вид: y=F(x,C1,C2,…,Cn)

Общее решение дифференциального уравнения 1_ого порядка имеет вид: y=F(x,С)

В отличие от общего решения дифференциального уравнения его частным решением называют всякую функцию, удовлетворяющую данному уравнению, но не содержащую произвольных постоянных.

Дифференциальные уравнения первого порядка с разделяющимися переменными, алгоритм их решения.

Уравнение с разделяющимися переменными имеет вид ___________________,причем его правая часть может быть представлена в виде произведения двух отдельных функций:_______________________________________________________________.Тогда:

 

Можно преобразовать это уравнение,разделив переменные справа и слева;

 

Общий вид уравнения с разделенными переменными:

 

Уравнение решается непосредственным интегрированием:слева по переменной y и справа по переменной х с прибавлением постоянной С.

 

Решая это уравнение найдем ответ:

 

7.Случайные события. Классическое и статистическое определения вероятности случайного события. Виды случайных событий

Случайным называется событие,наступление которого нельзя достоверно предвидеть. В одних и тех же доступных наблюдению условиях оно может произойти, может и не произойти.

Относительной частотой случайного события в данной серии испытаний или просто частотой случайного события А называют отношение:

Виды случайных событий:

1.Событие, которое при данном испытании произойдет обязательно, называется достоверным, его вероятность равна 1(например, достоверным является событие,состоящее в извлечении наугад упаковки аспирина из ящика, в котором находится только упаковка аспирина)

2.Событие, которое при данном испытании не может произойти, называется невозможным, его вероятность равна нулю(например, невозможным является событие, состоящее в извлечении наугад упаковки аспирина из ящика, в котором находятся только упаковки анальгина)

3.События называются несовместимыми, если появление любого из них в результате испытания исключает появления других.(например,если событие А1состоит в выпадении цифры 1 при однократном бросании игрального кубика, событие А2- в выпадении цифры 2 и т.д., то события являются несовместимыми, поскольку осуществление любого из них исключает наступление остальных событий в этом испытании)

4.События называются совместными,если появление любого из них в результате испытания не исключает появления остальных.(например,если событие А1 состоит в выпадении цифры 1 при однократном бросании игрального кубика,а событие А2- в выпадении нечетного числа очков, то эти два события являются совместными,поскольку 1 является нечетным числом)

5.Событие В называется благоприятствующим для события А, если при наступлении события В обязательно наступает событие А

6.Событие А и В называется независимыми,если вероятность наступления каждого из них не зависит от того, наступило ли при этом другое событие.(например,при одновременном подбрасывании двух монет случайное событие А,состоящее в выпадении герба у одной монеты, и событии В, состоящее в выпадении герба у другой монеты, являются независимыми событиями)

7.Событие В называется зависимым от события А,если вероятность наступления события В зависит от того, произошло ли событие А

8.Если два события единственно возможны и несовместимы, то их называют противоположными и обозначают А и Ā: Р(А)+Р(Ā)=1

9.Система событий А1,А2,…,Аn называется полной,если в результате испытания обязательно наступает только одно из этих событий. Сумма вероятностей событий, образующих ролнкю систему, равна единице: Р(А1)+Р(А2)+…..+Р(Аn)=1

Существуют классическое и статистическое определение вероятности события. Их основное отличие друг от друга состоит в том, что классическое определение вероятности основывается исключительно на умозаключениях и не предполагает проведения какого бы то ни было эксперимента, в то время как статистическое определение вероятностей, наоборот, не связано ни с какими рассуждениями, а основывается только лишь на проводимых многочисленных испытаниях.