
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная функции.Геометрический и механический смыслы производной.Производные основных элементарных функций.Производная сложной функции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Производная функции.Геометрический и механический смыслы производной.Производные основных элементарных функций.Производная сложной функции. Предел отношения приращения △у ФУНКЦИИ У=f(x) к приращению аргумента △x в заданной точке х0 при стремлении △х к нулю, называется производной функции в заданной точке. Обозначения производной: ______________________________ _______________________________________________,где
Нахождения производной функции называется дифференцированием. Дифференциирование основных элементарных функций проводится по формулам и правилам: 1,(u+v+w) '=u '+v '+w ' 2. (u v)=u '+v '+w ' 3.
Геометрический смысл производной. Величину тангенса угла наклона касательной,проведенной к графику функции,в математике называют угловым коэффицентом касательной. Угловой коэффицент касательной,проведенной к графику дифференцируемой функции в некоторой точке,численно равен производной функции в данной точке Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x (t) времени t. В течение интервала времени от t 0 до t 0 +
отсюда, v (t 0) = x’ (t 0), т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости повремени: a = v’ (t). Производная сложной функции.Из элементарных функций образуются сложные функции.Например,задана функция y=f(u),где u в свою очередб зависит от х, т.е u=φ(x). Тогда,при изменении х будут меняться u и y.В этом члучае заданная функция y=f(u) называется СЛОЖНОЙ и обозначается y=f{ φ(x)}.Величина u называется ПРОМЕЖУТОЧНОЙ ПЕРЕМЕННОЙ.тогда: y ' =y ' u * u ' x Дифференциал функции.Аналитический и геометрический смысл дифференциала Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента) и обознвчается dy
Дифференциал функции,в общем случае отличаясь от приращения функции,представляет собой главную часть этого приращения,линейную относительно приращения аргумента.В этом заключается аналитический смысл дифференциала
Дифференциал функции является приращением ординаты касательной(АВ), которое соответствует приращению D х (МВ) абсциссы. В этом заключается геометрический смысл дифференциала. Дифференциалом называют приращение аргумента,т.е dx= Δx
Первообразная функции. Неопределенный интеграл, его свойства. Таблица основных неопределенных интегралов. Функция F (x) называется первообразной для функции f (x) на интервале (a,b), если она дифференцируема на этом интервале и в каждой его точке F’(x)=f(x) Множество всех первообразных некоторой функции f (x) называется неопределенным интегралом функции f (x) и обозначается как
Функция f(x) называется подынтегральной функцией,f(x)dx- подынтегральным выражением Если F(x)- какая-нибудь первообразная функции f(x),то
где С - произвольная постоянная.
. Дифференциал от неопределенного интеграла равен подынтегральному выражению
Производная от неопределенного интеграла равна подынтегральной функции
Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная
Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла
Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций
5. Определенный интеграл. Формула Ньютона-Лейбница. Свойства определенного интеграла. Геометрический смысл определенного интеграла. Разность F(b)-F(a) или значение приращения любой первообразной от данной функции f(x) при изменении аргумента от x=a до x=b называется определенным интегралом функции f(x) в пределах от а до b: a ∫bf(x)dx =F(b)-F(a) это формула Ньютона-Лейбница
Свойства определенного интеграла.
5. Определенный интеграл от алгебраической суммы конечного числа функций, интегрируемых на отрезке [a,b], равен алгебраической сумме определенных интегралов этих функций на данном отрезке: Геометрический смысл определенного интеграла. Понятие дифференциального уравнения. Порядок уравнения, общее и частное решение дифференциального уравнения. Дифференциальные уравнения первого порядка с разделяющимися переменными, алгоритм их решения. Понятие дифференциального уравнения. Общий вид дифференциального уравнения первого порядка: F(x,y, y')=0 Общее решения дифференциального уравнения n-го порядка имеет вид: y=F(x,C1,C2,…,Cn) Общее решение дифференциального уравнения 1_ого порядка имеет вид: y=F(x,С)
Дифференциальные уравнения первого порядка с разделяющимися переменными, алгоритм их решения. Уравнение с разделяющимися переменными имеет вид ___________________,причем его правая часть может быть представлена в виде произведения двух отдельных функций:_______________________________________________________________.Тогда:
Можно преобразовать это уравнение,разделив переменные справа и слева;
Общий вид уравнения с разделенными переменными:
Уравнение решается непосредственным интегрированием:слева по переменной y и справа по переменной х с прибавлением постоянной С.
Решая это уравнение найдем ответ:
7.Случайные события. Классическое и статистическое определения вероятности случайного события. Виды случайных событий Случайным называется событие,наступление которого нельзя достоверно предвидеть. В одних и тех же доступных наблюдению условиях оно может произойти, может и не произойти. Относительной частотой случайного события в данной серии испытаний или просто частотой случайного события А называют отношение:
Виды случайных событий: 1.Событие, которое при данном испытании произойдет обязательно, называется достоверным, его вероятность равна 1(например, достоверным является событие,состоящее в извлечении наугад упаковки аспирина из ящика, в котором находится только упаковка аспирина) 2.Событие, которое при данном испытании не может произойти, называется невозможным, его вероятность равна нулю(например, невозможным является событие, состоящее в извлечении наугад упаковки аспирина из ящика, в котором находятся только упаковки анальгина) 3.События называются несовместимыми, если появление любого из них в результате испытания исключает появления других.(например,если событие А1состоит в выпадении цифры 1 при однократном бросании игрального кубика, событие А2- в выпадении цифры 2 и т.д., то события являются несовместимыми, поскольку осуществление любого из них исключает наступление остальных событий в этом испытании) 4.События называются совместными,если появление любого из них в результате испытания не исключает появления остальных.(например,если событие А1 состоит в выпадении цифры 1 при однократном бросании игрального кубика,а событие А2- в выпадении нечетного числа очков, то эти два события являются совместными,поскольку 1 является нечетным числом) 5.Событие В называется благоприятствующим для события А, если при наступлении события В обязательно наступает событие А 6.Событие А и В называется независимыми,если вероятность наступления каждого из них не зависит от того, наступило ли при этом другое событие.(например,при одновременном подбрасывании двух монет случайное событие А,состоящее в выпадении герба у одной монеты, и событии В, состоящее в выпадении герба у другой монеты, являются независимыми событиями) 7.Событие В называется зависимым от события А,если вероятность наступления события В зависит от того, произошло ли событие А 8.Если два события единственно возможны и несовместимы, то их называют противоположными и обозначают А и Ā: Р(А)+Р(Ā)=1 9.Система событий А1,А2,…,Аn называется полной,если в результате испытания обязательно наступает только одно из этих событий. Сумма вероятностей событий, образующих ролнкю систему, равна единице: Р(А1)+Р(А2)+…..+Р(Аn)=1 Существуют классическое и статистическое определение вероятности события. Их основное отличие друг от друга состоит в том, что классическое определение вероятности основывается исключительно на умозаключениях и не предполагает проведения какого бы то ни было эксперимента, в то время как статистическое определение вероятностей, наоборот, не связано ни с какими рассуждениями, а основывается только лишь на проводимых многочисленных испытаниях. Статистический ряд Пусть требуется изучить распределение значений признака Х у объектов некоторой генеральной совокупности. Для этого из генеральной совокупности извлекают некоторую выборку объемом n. Пусть в полученной выборочной совокупности наименьшее значение признака x1 встречается m1 раз, следующее по величине значение x2-m2 раз,……., xk- mk раз. Наблюдаемые значения признака называются вариантами, а числа m1,m2,m3,…..,mk- их частотами. Очевидно, что сумма всех частот равна объему выборки: m1 + m2 +….mk =________________________, Результаты наблюдений представим в виде таблицы, в первой строке которой в порядке возрастания перечислены все варианты, во второй – соответствующие им частоты:
Такая таблица называется статистическим дискретным рядом распределения. Для графического изображения такого ряда на координатной плоскости откладывают точки (xi; mi) и соединяют их отрезками прямых Полученная ломаная линия, являющаяся графическим изображением дискретного статистического ряда распределения, называется полигоном частот.
Наряду с частотами mi часто применяются относительные частоты Pi=,_________ сумма которых равна единице:
_______________________ Ультразвуковая эхолокация Рассмотрим отражение УЗ-волны от границы раздела двух сред с различными свойствами
где Iотр - интенсивность отраженной УЗ-волны, I0 - интенсивность падающей; Iпрош (рис.5) - интенсивность волны, прошедшей во вторую среду. R -это безразмерная величина, принимающая значения в интервале от нуля (отсутствие отражения) до единицы (полное отражение). В случае нормального падения волны на границу раздела (рис.5), этот коэффициент можно найти по формуле
где ρ1 и ρ2 - плотности первой и второй среды соответственно; v1 и v2 - скорости УЗ в этих средах. На явлении отражения УЗ от границы раздела сред основана эхолокация – метод локализации неоднородностей в средах
Источник УЗ посылает ультразвуковой сигнал в импульсном режиме. После нескольких импульсов наступает пауза, в течение которой источник «ожидает» прихода отраженной волны. На экране локатора фактически представлена временная зависимость электрического напряжения, соответствующего посланному и зарегистрированному после отражения УЗ-сигналу. Зная интервал времени между импульсом посылки и отраженным импульсом (рис.6, б), а также скорость волны, можно найти расстояние от источника до границы отражения:
На комплексном действии механических, тепловых и химических факторов основано биологическое действие ультразвука, который может вызвать гибель вирусов, бактерий и грибков, а при значительной мощности и мелких животных. При незначительной мощности УЗ повышает проницаемость клеточных мембран, активизирует процессы тканевого обмена. Ультразвук в настоящее время получил разнообразные применения. В фармацевтической промышленности при изготовлении лекарств используется способность ультразвука дробить тела,помещенные в жидкость и создавать эмульсии При лечении туберкулеза,бронхиальной астмы применяют аэрозоли различных лекарственных средств, полученных с помощью ультразвука В медицине УЗ в различных диапозонах частот используется для терапевтического и хирургического лечения и диагностики Метод лечения,при котором используются колебания 800-3000кГц называется ультразвуковой терапией Для лечебных целей применяют аппараты,в которых электрический ток подается на пластинку излучателя = кварца или титанита бария.Пластинка под действием переменного электрического тока сжимается и разжимается. Движения пластинки через контактную среду (вода,вазелиновое масло, передаются на подлежащие ткани.УЗ в этих частотах распространяется в средах почти прямолинейным пучком,что позволяет воздействовать им на ограниченный участок и проникает на глубину от 1 до 5-6 см.Это дает возможность использовать его для лечения заболеваний различных органов В лечебной практике используют в основном малые дозы ультразвука, активизирующие внутриклеточные процессы в тканях (биосинтез белка, усиление активности ферментов и т.д.). Терапевтические дозы ультразвука оказывают выраженное болеутоляющее, сосудорасширяющее, противовоспалительное действие. Под влиянием ультразвука в зоне воздействия повышается проницаемость кожи и слизистых оболочек, что способствует введению в ткани через кожу нанесенных на нее лекарственных средств. Этот метод называется фонофорезом. Существует аппарат для ультразвуковой сварки и резки костей Способность ультразвуковых волн без существенного поглощения проникать в мягкие ткани организма и отражаться от уплотнений и неоднородностей используется в диагностических целях. Ультразвуковая диагностика дополняет основной метод исследования внутренних органов – рентгенодиагностику, а иногда имеет преимущества над ней. Высокая чувствительность ультразвуковой аппаратуры позволяет получить эхограмму мягких тканей, последить за движущимися объектами, например, за частотой сердечных сокращений, скоростью кровотока в крупных сосудах. Биологическое действие ультразвука, т.е. изменения, вызываемые в жизнедеятельности и структурах биологических объектов при воздействии на них ультразвука, определяется, главным образом, его интенсивностью и длительностью облучения и может оказывать как положительное, так и отрицательное влияние на жизнедеятельность организмов.
Перенос частиц через мембраны. Уравнение Фика. Применение уравнения Фика к биологической мембране. Уравнение Нернста-Планка. Важной характеристикой мембран является их способность пропускать или не пропускать молекулы, атомы и ионы. Эти вопросы относятся к явлениям переноса. Рассмотрим наиболее важные для биологических мембран явления: перенос вещества (диффузию) и перенос заряда (электропроводность).В биофизике также используется термин «транспорт частиц» Основное уравнение диффузии имеет вид:
Это уравнение Фика:I- плотность потока частиц,D- коэффицент диффузии D=___ __________, σ- среднее расстояние между молекулами, m-масса молекулы, n-концентрация молекул,с=m*n-массовая концентрация, τ - среднее время оседлой жизни молекулы Если бы диффузия была единственным процессом, управляющим движением ионов через мембрану, то через некоторое время установилось бы равновесное отношение концентраций. Но помимо диффузии действуют также системы активного транспорта – натрий-калиевые насосы, и их действие противоположно направлению нормальной диффузии. Рассмотрим распространение потенциала действия в нервном волокне. Нервная клетка или нейрон состоит из клеточного тела и выроста, называемого аксоном. Нейрон можно привести в возбужденное состояние в любой точке аксона электрическим, химическим или механическим способом. Тепловое Законы теплового излучения. Формула Планка. Тепловое (температурное) излучение обусловлено возбуждением атомов и молекул при их соударениях в процессе теплового движения. Оно является универсальным явлением и происходит при любой температуре, отличной от абсолютного нуля. При этом тела не только излучают, но и поглощают энергию от окружающих тел и атомов, находящихся в глубине самого тела. Если тело (или система тел) в результате поглощения излучения или других процессов получает в единицу времени столько же энергии, сколько отдает путем излучения, то излучение называется равновесным. Равновесное излучение имеет место в изолированной системе тел, когда в процессе теплообмена в ней устанавливается постоянная температура. Электромагнитное излучение, занимающие спектральную область от 380 нм до 10 нм (от фиолетовой границы видимого света до длинноволнового рентгеновского излучения) называется ультрафиолетовым (УФ) излучением. Оно делится на 2 области: от 380 до 200 нм – ближнее или флуоресцентное УФ-излучение; от 200 до 10 нм – дальнее или вакуумное. УФ-излучение поглощается простым стеклом, а при длине волны меньше 200 нм поглощается тонким слоем любого вещества, включая воздух. УФ-излучение оказывает сильное биологическое действие на живые организмы, которое может быть и полезным, и вредным. Его первичное действие связано с фотохимическими реакциями, происходящими в тканях при поглощении излучения. В ткани оно проникает на глубину до 1 мм и проявляется на месте воздействия эритемой. В соответствии с особенностями биологического действия выделяют следующие зоны УФ-излучения: Зона А (380-315 нм) – антирахитная – отличается укрепляющим и закаливающим организм действием. Используется в профилактических и гигиенических целях. Зона В (315-280 нм) – эритемная – характеризуется эритемным действием и используется в лечебных целях. Зона С (280-200 нм) – бактерицидная – отличается бактерицидным действием; используется в качестве средства дезинфекции. Лазерная эндоскопия Лазерный пробой . 48.Рентгеновское излучение.Устройство рентгеновской трубки. Тормозное рентгеновское излучение. Характеристическое рентгеновское излучение. Закон Мозли. Рентгеновским излучением называют электромагнитные волны с длинной волны от 80 до 10-5.нм Рентгеновское излучение возникает в результате преобразования кинетической энергии ускоренных электронов в энергию электромагнитных волн.
Самым распространенным источником рентгеновского излучения является рентгеновская трубка. Она состоит из наполненного маслом кожуха с колбой. Колба представляет собой вакуумный сосуд из термостойкого стекла, внутри которого находится накапливаемый катод и анод. При торможении электронов в аноде возникает тормозное рентгеновское излучение. С движущимся электрическим зарядом связано магнитное поле, индукция которого зависит от скорости электрона. При торможении уменьшается магнитная индукция и появляется электромагнитная волна. Тормозное излучение дает сплошной спектр, который называют белым рентгеновским излучением. Его спектральная интенсивность при различных напряжениях на трубке представлена кривыми
Формула определения которой: eU = hvmax Поток рентгеновского излучения вычисляется по формуле: Ф = kIU2Z – гдеU и Z – напряжение и сила тока в рентгеновской трубке; Z – порядковый номер атома вещества.
Если увеличивать напряжение на трубке выше определенного предела, то на сплошное излучение накладываются узкие спектральные линии, составляющее характеристическое рентгеновское излучение. Производная функции.Геометрический и механический смыслы производной.Производные основных элементарных функций.Производная сложной функции. Предел отношения приращения △у ФУНКЦИИ У=f(x) к приращению аргумента △x в заданной точке х0 при стремлении △х к нулю, называется производной функции в заданной точке. Обозначения производной: ______________________________ _______________________________________________,где
Нахождения производной функции называется дифференцированием. Дифференциирование основных элементарных функций проводится по формулам и правилам: 1,(u+v+w) '=u '+v '+w ' 2. (u v)=u '+v '+w ' 3.
Геометрический смысл производной. Величину тангенса угла наклона касательной,проведенной к графику функции,в математике называют угловым коэффицентом касательной. Угловой коэффицент касательной,проведенной к графику дифференцируемой функции в некоторой точке,численно равен производной функции в данной точке Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x (t) времени t. В течение интервала времени от t 0 до t 0 +
отсюда, v (t 0) = x’ (t 0), т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости повремени: a = v’ (t). Производная сложной функции.Из элементарных функций образуются сложные функции.Например,задана функция y=f(u),где u в свою очередб зависит от х, т.е u=φ(x). Тогда,при изменении х будут меняться u и y.В этом члучае заданная функция y=f(u) называется СЛОЖНОЙ и обозначается y=f{ φ(x)}.Величина u называется ПРОМЕЖУТОЧНОЙ ПЕРЕМЕННОЙ.тогда: y ' =y ' u * u ' x
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 861; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.011 с.) |

 точка перемещается на расстояние: x (t 0 +
точка перемещается на расстояние: x (t 0 + 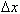 , а её средняя скорость равна: va =
, а её средняя скорость равна: va =  0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v (t 0) материальной точки в момент времени t 0. Но по определению производной мы имеем:
0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v (t 0) материальной точки в момент времени t 0. Но по определению производной мы имеем:



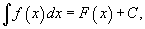




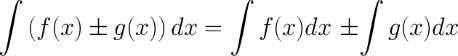




 Для количественной характеристики процесса вводится понятие коэффициента отражения
Для количественной характеристики процесса вводится понятие коэффициента отражения







