Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное свойство кривой второго порядка.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
36) Понятие функции. Область определения и область значения. График функции.
Основные свойства функции. (четность/ нечетность, монотонность, периодичность, ограниченность). Обратная функция. Сложная функция.
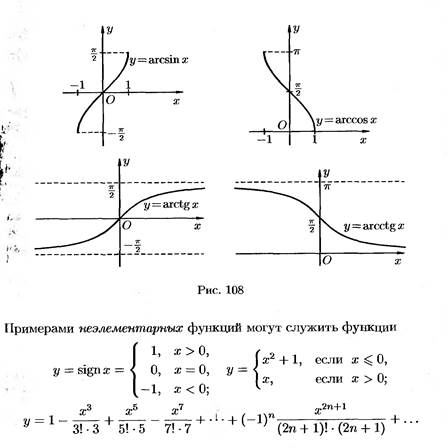
Основные элементарные функции и их графики.
Понятие окрестности точки. Предел функции (по Коши). Основные теоремы о пределах. Окре́стность точки — множество, содержащее данную точку, и близкие (в каком-либо смысле) к ней. Пусть ε > 0 произвольное фиксированное число. Окрестностью точки x 0 на числовой прямой (иногда говорят ε-окрестностью) называется множество точек, удаленных от x 0 не более чем на ε, т.е. O ε(x 0) = { x: | x − x 0 | < ε}.
Основные теоремы о пределах Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела. Следствие. Если две функции f (x) и g (x) равны в некоторой окрестности точки Теорема 2. Если функцииf(x) и g(x) имеют пределы в точке 1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
2) предел произведения функций равен произведению пределов сомножителей, т.е.
3) предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
Замечание. Формулы (2) и (3) справедливы для любого конечного числа функций. Следствие 1. Предел постоянной равен самой постоянной, т.е.
Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.
Теорема 3 (о пределе сложной функции). Если существует конечный предел
а функцияf(u) непрерывна в точке
Другими словами, для непрерывных функций символы предела и функции можно поменять местами. Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.
Бесконечно малые функции. Их свойства и сравнение БМФ.
1) Сумма фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а. 2) Произведение фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а. 3) Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х®а. 4) Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.
Сравнение бесконечно малых функций Пусть a(х), b(х) и g(х) – бесконечно малые функции при х ® а. Будем обозначать эти функции a, b и g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.Например, функция f(x) = x10 стремится к нулю быстрее, чем функция f(x) = x. Первый замечательный предел, Второй замечательный предел
Эквивалентные, бесконечно малые функции
Односторонние пределы. Понятие непрерывности функции. Точки разрыва и их классификации. Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (или преде́лом спра́ва).
Определение производное функции. Механический и геометрический смысл производной.
Уравнение касательной и нормали к кривой.
Правила дифференцирования. Основные правила дифференцирования Пусть
7) Если
Производная сложной и обратной функции.
Производные основных элементарных функций. Таблица производных.
Дифференцирование неявной функции и функции, заданной параметрически.
Логарифмическое дифференцирование.
|
||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 526; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |













 , за исключением, может быть, самой точки
, за исключением, может быть, самой точки  , либо обе не имеют предела в этой точке.
, либо обе не имеют предела в этой точке.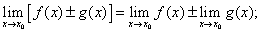 (2)
(2)
 (3)
(3) (4)
(4)


 , то
, то





















 , тогда:
, тогда:
 , то есть
, то есть  , где
, где  и
и  имеют производные, то
имеют производные, то  (правило дифференцирования сложной функции).
(правило дифференцирования сложной функции).