
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение координат середины отрезка. Нахождение координат точки, делящей отрезок в данном отношении.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Есть две произвольные точки A1(x1;y1;z1) и A2(x2;y2;z2). Тогда серединой отрезка A1A2 будет точка С с координатами x, y, z, где
26) Каноническое уравнение прямой (вывод). Параметрическое задание прямой. Уравнение прямой через две точки (вывод). Каноническое уравнение прямой в пространстве:
где
Параметрическое уравнение прямой в пространстве:
27) Общее уравнение прямой и его частные случаи. Условия параллельности и перпендикулярности прямых заданных в общем виде. Направляющий и нормальный вектор прямой. Нахождение их координат из общего уравнения прямой.
Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства A 1 A 2 + B 1 B 2 = 0.
Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором. Найти уравнение прямой с направляющим вектором
Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В. 28) Уравнение прямой в отрезках (вывод) Уравнение прямой с угловым коэфицентом. Геометрический смысл углового коэффицента прямой.
Уравнение прямой через точку с данным угловым коэффициентом. Условия параллельности и перпендикулярности прямых, заданных с угловым коэффициентом.
Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k 1 = k 2 В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
Уравнение прямой в полярной системе координат. Уравнение прямой через точку с данным нормальным вектором.
Нормальное уравнение прямой. Приведение общего уравнения прямой к нормальному виду. Расстояние от точки до прямой. Расстояние между двумя параллельными прямыми.
Расстоянием между параллельными прямыми называется часть перпендикуляра к этим параллельным прямым заключенная между ними Определение и каноническое уравнение эллипса. Свойства эллипса.
Свойства: Точки пересечения эллипса с осями,называются вершинами. (большая ось- фокальная и малая ось) Из канонического уравнения следует что
Эллипс лежит внутри прямоугольника со сторонами 2a и 2b. Т.к. уравнение эллипса содержит только квадраты переменных то, если точка с координатами (x;y) принадл. Э, то точка с коорд. (-x;y) и (x;-y) и(-x;-y) принадлежат Э. след. Эллипс симметричен относительно Ox, Oy, начала координат. Эксцентриситет эллипса. Это отношение фокусного расстояния к длине большой оси
Этот показатель характеризует форму эллипса
Чем меньше Е тем Эллипс больше приближается к окружности. Если Е=0 эллипс превращается в окружность x^2+y^2=a^2 Директрисы эллипса. Это прямые которые перпендикулярны фокальной оси и находятся на расстоянии a/E от ее центра x= +/- a/E R1+R2=2a R1,R2- фокальные радиусы Для фокальных радиусов имеют место формулы
Основное свойство. Отношение расстояния от произвольной точки эллипса до фокуса к расстоянию до соответствующей директрисы есть величина постоянная равная ексцентриситету.
Определение и каноническое уравнение гиперболы. Свойства гиперболы. Асимптоты гиперболы.
Свойства:
Гипербола лежит вне прямоугольника со сторонами 2a и 2b. Эксцентриситет гиперболы. E=c/a E>1 B^2=c^2-a^2
Чем меньше E тем меньше отношение е полуосей,тем больше вытягивается прямоугольник, ветви приближаются к осям,сжаты. 5. Директрисы
Основное свойство.
Определение и каноническое уравнение параболы. Свойства параболы.
|
||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.112.208 (0.007 с.) |





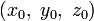 — координаты некоторой фиксированной точки M 0, лежащей на прямой;
— координаты некоторой фиксированной точки M 0, лежащей на прямой;  — координаты вектора, коллинеарного этой прямой.
— координаты вектора, коллинеарного этой прямой.






 (9)
(9)

 (1, -1) и проходящей через точку А(1, 2).
(1, -1) и проходящей через точку А(1, 2).


































