Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрицы, виды, действия над ними.Содержание книги
Поиск на нашем сайте
Матрицы, виды, действия над ними.
2) Произведение матриц, свойства, элементарные преобразования матриц.
Определитель квадратной матрицы. Вычисление определителя 2-го порядка. Вычисление определителя 3-го порядка. Правило Саррюса.
Свойства определителей не связанные с понятием алгебраического дополнения.
Минор и алгебраическое дополнение. Разложение определителя по строке.
Вырожденные и невырожденные матрицы. Обратная матрица(свойства, вычисление).
Ранг матрицы. Вычисление ранга матрицы.
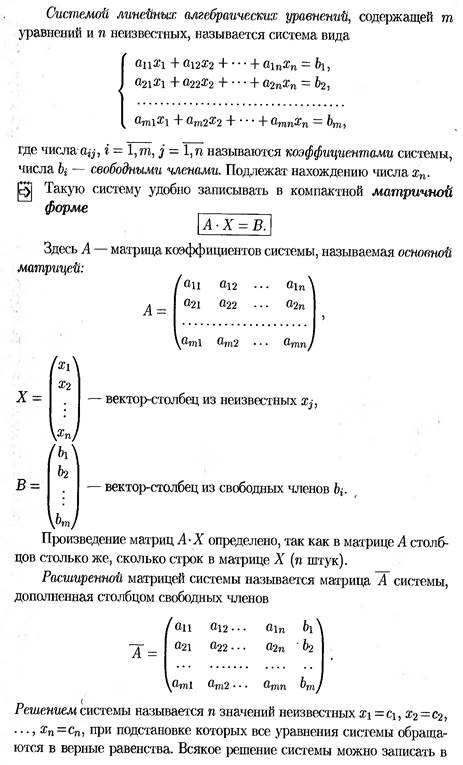
СЛАУ, совместная система, определенная система, понятие «решить систему», общее и частное решение СЛАУ. Матричная форма записи СЛАУ. Решение СЛАУ с помощью обратной матрицы.
Метод обратной матрицы (Матричный метод) решения систем линейных алгебраических уравнений с ненулевым определителем основной матрицы состоит в поиске матрицы, обратной к основной матрице, и умножению ее на матрицу свободных членов.
При решении систем уравнений методом обратной матрицы используются вычисления определителя матрицы (Для вычисления матрицы, обратной к основной матрице системы уравнений). Для того, чтобы матрица имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля, тоесть матрица должна быть невырожденной.
СЛАУ с квадратной невырожденной матрицей. Формулы Крамера.
Невырожденная матрица (система) — квадратная матрица (система), определитель которойD=detА не равен нулю. Квадратная матрица — матрица, у которой число строк равно числу столбцов.
Метод Гаусса для решения СЛАУ.
Совместность СЛАУ. Теорема Кронекера-Капелли. Критерий определенности СЛАУ.
Однородная система линейных уравнений.
Понятие вектора. (длина, единичный,нуль- вектор). Равные, противоположные, орт-вектор)
14) Коллинеарные векоры (сонаправленные, противоположнонаправленные) Признак коллинеарности, компланарные вектора.
Признаком коллинеарности двух векторов является пропорциональность их координат
15) Сложение векторов. (правило треугольника, параллелограмма, многоугольника). Разность векторов, умножение вектора на число.
Базис векторного пространства. Разложения вектора по ортам координатных осей. Понятие координат вектора. Называется такая система векторов,которая: Задана в определенном порядке Линейно не зависима Любой вектор пространства является линейной комбинацией данной системы векторов. Числа стоящие перед базисными векторами называются координатами вектора в данном базисе. Определение. Базисом векторного пространства
рис.2.
Замечание. Базис векторного пространства не может содержать нулевого вектора: в пространстве
Координаты и Модуль вектора,заданные координатами начала и конца. Действия над векторами,заданными своими координатами (сложение, вычитание, умножение на число, равенство, коллинеарность).
Направляющие косинусы векторов. Равенство их связывающее.
Скалярное произведение векторов и его свойства. Выражение скалярного произведения через координаты.
Угол между векторами. Признак перпендикулярности векторов.
Векторное произведение векторов и его свойство. Выражение векторного произведения через координаты. Геометрические приложения векторного произведения.
Смешанное произведение векторов и его свойство. Выражение смешанного произведения через координаты. Геометрические приложения смешанного произведения.
27) Общее уравнение прямой и его частные случаи. Условия параллельности и перпендикулярности прямых заданных в общем виде. Направляющий и нормальный вектор прямой. Нахождение их координат из общего уравнения прямой.
Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства A 1 A 2 + B 1 B 2 = 0.
Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором. Найти уравнение прямой с направляющим вектором
Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В. 28) Уравнение прямой в отрезках (вывод) Уравнение прямой с угловым коэфицентом. Геометрический смысл углового коэффицента прямой.
Т.к. уравнение эллипса содержит только квадраты переменных то, если точка с координатами (x;y) принадл. Э, то точка с коорд. (-x;y) и (x;-y) и(-x;-y) принадлежат Э. след. Эллипс симметричен относительно Ox, Oy, начала координат. Эксцентриситет эллипса. Директрисы эллипса. Это прямые которые перпендикулярны фокальной оси и находятся на расстоянии a/E от ее центра x= +/- a/E R1+R2=2a R1,R2- фокальные радиусы Основное свойство. Эксцентриситет гиперболы. E=c/a E>1 B^2=c^2-a^2
Директрисы
Основное свойство.
Основные теоремы о пределах Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела. Следствие. Если две функции f (x) и g (x) равны в некоторой окрестности точки Теорема 2. Если функцииf(x) и g(x) имеют пределы в точке 1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
2) предел произведения функций равен произведению пределов сомножителей, т.е.
3) предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
Замечание. Формулы (2) и (3) справедливы для любого конечного числа функций. Следствие 1. Предел постоянной равен самой постоянной, т.е.
Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.
Теорема 3 (о пределе сложной функции). Если существует конечный предел
а функцияf(u) непрерывна в точке
Другими словами, для непрерывных функций символы предела и функции можно поменять местами. Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.
Правила дифференцирования. Производные основных элементарных функций. Таблица производных.
Матрицы, виды, действия над ними.
2) Произведение матриц, свойства, элементарные преобразования матриц.
|
||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 666; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |





































 называется любая упорядоченная тройка некомпланарных векторов (т.е. не лежащих в одной плоскости) пространства
называется любая упорядоченная тройка некомпланарных векторов (т.е. не лежащих в одной плоскости) пространства 
 – базис
– базис  по определению, в пространстве
по определению, в пространстве 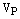 двавектора будут коллинеарные, если хотя бы один из них нулевой, впространстве
двавектора будут коллинеарные, если хотя бы один из них нулевой, впространстве 
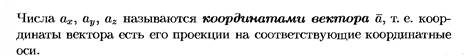

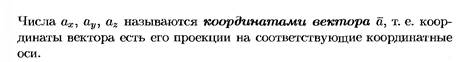


















 (9)
(9)

 (1, -1) и проходящей через точку А(1, 2).
(1, -1) и проходящей через точку А(1, 2).







 , за исключением, может быть, самой точки
, за исключением, может быть, самой точки  , либо обе не имеют предела в этой точке.
, либо обе не имеют предела в этой точке.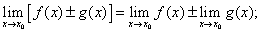 (2)
(2)
 (3)
(3) (4)
(4)


 , то
, то