
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действия над векторами, заданными своими координатамиСодержание книги
Поиск на нашем сайте Определение 3.4 Проекцией вектора Точки
Основные свойства проекции: 1) 2) 3) 4) Рассмотрим в пространстве прямоугольную систему координат
Единичные векторы Произвольный вектор
а значит, существуют числа
Следовательно, вектор
Формула (3.5) называется разложением вектора Векторное равенство (3.5) записывают в виде
Имеет место аналогичное разложение вектора
Длина вектора
Для плоского вектора
Направление вектора
Справедливо равенство
При выполнении линейных операций над векторами тем же операциям подвергнутся и их проекции на координатные оси. Пусть даны два вектора При сложении векторов их одноименные координаты складываются, при вычитании – вычитаются, при умножении на число – умножаются на это число:
Векторы
Векторы
Радиус-вектором точки Координаты точки – это координаты её радиус-вектора Для вектора
Здесь Деление отрезка в данном отношении Определим радиус-вектор Вектор откуда Из равенства векторов (3.16) следуют три координатных формулы
Для
Скалярное произведение векторов Определение 3.5 Скалярным произведением двух ненулевых векторов Таким образом
где
Из рисунка видно:
С учетом (3.20) можно записать равенства
Свойства скалярного произведения: 1) 2) 3) 4) 5) Условие перпендикулярности векторов. Если векторы В частности
Скалярное произведение в координатной форме Пусть векторы
То есть, если векторы
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1023; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 на ось
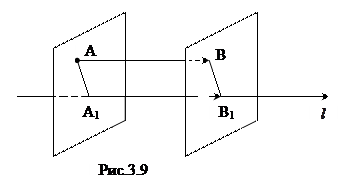
на ось  называется число, равное длине вектора
называется число, равное длине вектора  (рис. 3.9), взятое со знаком «плюс», если направление вектора
(рис. 3.9), взятое со знаком «плюс», если направление вектора 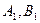 - это точки пересечения оси
- это точки пересечения оси 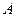 и
и  , перпендикулярно оси
, перпендикулярно оси  .
.
 , где
, где 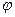 - угол между вектором
- угол между вектором  и осью
и осью  ;
;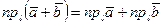 ;
; .
.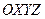 . Построим на координатных осях
. Построим на координатных осях  и
и  единичные векторы, обозначаемые
единичные векторы, обозначаемые  соответственно (рис. 3.10).
соответственно (рис. 3.10).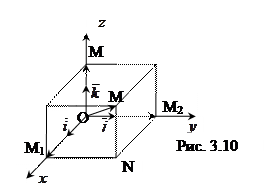
 вектора
вектора  ,
, 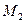 и
и  точки пересечения этих плоскостей с осями
точки пересечения этих плоскостей с осями 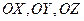 соответственно. Тогда
соответственно. Тогда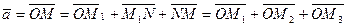 ,
, ,
,  ,
,  .
. , такие что
, такие что ,
, 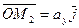 ,
,  и
и ,
,  ,
, 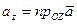 .
.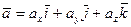 . (3.5)
. (3.5) . Коэффициенты
. Коэффициенты 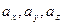 линейной комбинации (3.5) называют прямоугольными координатами вектора
линейной комбинации (3.5) называют прямоугольными координатами вектора  (3.6)
(3.6) на плоскости (рис. 3.11).
на плоскости (рис. 3.11).
 . (3.7)
. (3.7) определяется по формуле
определяется по формуле . (3.8)
. (3.8)
 . (3.9)
. (3.9) - углы, которые составляет вектор
- углы, которые составляет вектор  ,
, 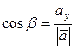 ,
, 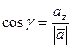 . (3.10)
. (3.10)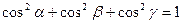 . (3.11)
. (3.11) и
и 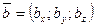 .
. , (3.12)
, (3.12) .
. равны тогда и только тогда, когда равны их соответствующие координаты:
равны тогда и только тогда, когда равны их соответствующие координаты: ,
, 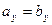 ,
,  . (3.13)
. (3.13) . (3.14)
. (3.14)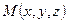 называется вектор
называется вектор  (рис. 3.12), начало которого совпадает с началом координат, а конец с точкой
(рис. 3.12), начало которого совпадает с началом координат, а конец с точкой 

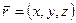 .
. , заданного координатами точки
, заданного координатами точки  и
и  , его координаты определяются из векторного равенства
, его координаты определяются из векторного равенства (3.15)
(3.15) и
и  - радиус-векторы точек
- радиус-векторы точек 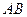 равны разностям одноименных координат конечной
равны разностям одноименных координат конечной  точки
точки  .
.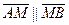 и одинаково направлен с
и одинаково направлен с  , поэтому
, поэтому  . Учитывая векторные равенства
. Учитывая векторные равенства  ,
,  получим
получим  ,
, (3.16)
(3.16) ,
,  ,
,  . (3.17)
. (3.17) (
( ,
, 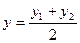 ,
,  . (3.18)
. (3.18) , равное произведению длин этих векторов на косинус угла
, равное произведению длин этих векторов на косинус угла 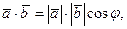 (3.19)
(3.19)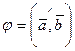 .
.
 ,
, 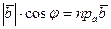 . (3.20)
. (3.20) . (3.21)
. (3.21) (коммутативный закон);
(коммутативный закон); (дистрибутивный закон);
(дистрибутивный закон); (ассоциативный по отношению к скалярному множителю);
(ассоциативный по отношению к скалярному множителю); , скалярный квадрат вектора
, скалярный квадрат вектора  .
.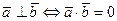 (3.22)
(3.22)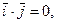

 .
. . Перемножая векторы как многочлены с учетом распределительного закона умножения и свойств скалярного произведения базисных векторов, получим:
. Перемножая векторы как многочлены с учетом распределительного закона умножения и свойств скалярного произведения базисных векторов, получим: . (3.23)
. (3.23) , то их скалярное произведение равно сумме произведений одноименных координат.
, то их скалярное произведение равно сумме произведений одноименных координат.


