
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плотность распределения вероятностей непрерывной случайной величины и ее свойства. Основные числовые характеристики непрерывной случайной величины.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Плотностью распределения вероятностей (плотностью вероятности) f(x) непрерывной случайной величины Х называется производная функции распределения F(x) этой величины: f(x)=F’(x) Свойства плотности распределения вероятностей: 1) Плотность вероятности является неотрицательной функцией: f(x)≥0; 2) Вероятность того, что в результате испытания непрерывная случайная величина примет какие либо значения из интервала (a,b) равна: Под основными числовыми характеристиками непрерывной случайной величины понимают, математическое ожидание, дисперсию и среднее квадратическое отклонение. Математическое ожидание непрерывной случайной величины: Дисперсия непрерывной случайной величины D(X) = M[X – M(X)]2. (добавить)
Среднее квадратическое отклонение: σ(х)= √D(X) Нормальный закон распределения. Вероятность попадения нормально распределенной случайнойвеличиныв заданный интервал.Правило трех сигм. Из всех видов распределения непрерывных случайных величин наиболее часто используют нормальное распределение, которое задается законом Гаусса. Так, если мы имеем сумму большого числа независимых величин, подчиненных каким угодно законам распределения, то при некоторых общих условиях она будет приближенно подчиняться нормальному закону. Непрерывная случайная величина называется распределенной по нормальному закону, если ее плотность вероятности имеет вид:
Подставив выражение примет значение из заданного интервала: P(a<X<b) =____________________
Правило трех сигм: отклонения значений нормального распределения случайной величины от ее математического ожидания по абсолютной величине практически не превышает ее утроенного среднего квадратического отклонения. Статистическая совокупность.Генеральная и выборочная статистические совокупности. Статистический дискретный ряд распределения.Полигоны частот и относительных частот. Статистическая совокупность - это множество объектов, характеризуемых некоторым качественным или количественным признаком. Генеральная статистическая совокупность- статистическая совокупность,состоящая из всех объектов,которые подлежат обследованию.Число объектов генеральной совокупности называют ее объемом и обозначают N Статистическая совокупность, состоящая из некоторого количества объектов, случайным образом отобранных из соответствующей генеральной совокупности, называется выборочной статистической совокупностью(выборкой) Число объектов выборки называют ее объемом и обозначают n Статистический ряд Пусть требуется изучить распределение значений признака Х у объектов некоторой генеральной совокупности. Для этого из генеральной совокупности извлекают некоторую выборку объемом n. Пусть в полученной выборочной совокупности наименьшее значение признака x1 встречается m1 раз, следующее по величине значение x2-m2 раз,……., xk- mk раз. Наблюдаемые значения признака называются вариантами, а числа m1,m2,m3,…..,mk- их частотами. Очевидно, что сумма всех частот равна объему выборки: m1 + m2 +….mk =________________________, Результаты наблюдений представим в виде таблицы, в первой строке которой в порядке возрастания перечислены все варианты, во второй – соответствующие им частоты:
Такая таблица называется статистическим дискретным рядом распределения. Для графического изображения такого ряда на координатной плоскости откладывают точки (xi; mi) и соединяют их отрезками прямых Полученная ломаная линия, являющаяся графическим изображением дискретного статистического ряда распределения, называется полигоном частот.
Наряду с частотами mi часто применяются относительные частоты Pi=,_________ сумма которых равна единице:
_______________________
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 2462; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.247.221 (0.009 с.) |

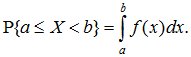 3) Определенный интеграл в пределах от –бесконечности до + бесконечности от плотности вероятности непрерывной случайной величины равен единице:
3) Определенный интеграл в пределах от –бесконечности до + бесконечности от плотности вероятности непрерывной случайной величины равен единице:  4) Определенный интеграл в пределах от минус бесконечности до х от плотности вероятности непрерывной случайной величины равен функции распределения этой величины:
4) Определенный интеграл в пределах от минус бесконечности до х от плотности вероятности непрерывной случайной величины равен функции распределения этой величины: 

 (увеличить,дописать), где М-математическое ожидание, σ в квадрате – дисперсия, σ-среднее квадратическое отклонение этой величины.это кривая Гаусса:
(увеличить,дописать), где М-математическое ожидание, σ в квадрате – дисперсия, σ-среднее квадратическое отклонение этой величины.это кривая Гаусса:




