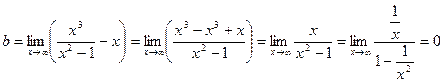Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные действия над матрицами.Содержание книги
Поиск на нашем сайте
Основные действия над матрицами.
Если число столбцов матрицы равно числу строк (
Единичная матрица:
Диагональная матрица:
Если Суммой (разностью) матриц является матрица, элементами которой являются сумма (разность) соответствующих элементов исходных матриц:
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число. Пример. Даны матрицы А и B, найти 2А + В.
Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Пример. Найти произведение матриц
Матрицу
другими словами, Определители. Для матрицы первого порядка определителем является сам единственный элемент этой матрицы:
Для матрицы 2х2 определитель определяется как
Для матрицы nxn определитель задаётся формулой:
где Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:
Пример. Вычислить определитель матрицы
Или если вычислять по второй строке:
Матричный метод решения систем линейных уравнений.
Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.
Пусть дана система уравнений:
Составим матрицы:
Систему уравнений можно записать:
Для применения данного метода необходимо находить обратную матрицу. Пример. Решить систему уравнений:
Найдем обратную матрицу.
Миноры:
Находим матрицу Х.
Итого решения системы: x =1; y = 2; z = 3.
Метод Крамера.
Теорема. Система из n уравнений с n неизвестными
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
где D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Пример. Найти решение системы уравнений:
Элементарные преобразования систем.
Метод Гаусса.
В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных. Рассмотрим систему линейных уравнений:
Разделим обе части 1–го уравнения на a11 ¹ 0, затем: 1) умножим на а21 и вычтем из второго уравнения 2) умножим на а31 и вычтем из третьего уравнения и т.д.
Получим:
где
Далее повторяем эти же действия для второго уравнения, потом для третьего и т.д.
Пример. Решить систему линейных уравнений методом Гаусса.
Составим расширенную матрицу системы.
Таким образом, исходная система может быть представлена в виде:
Векторная алгебра и аналитическая геометрия.
Элементы векторной алгебры.
Вектором называется направленный отрезок (упорядоченная пара точек).
Длиной (модулем) вектора называется расстояние между началом и концом вектора.
Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Векторы называются компланарными, если существует плоскость, которой они параллельны.
Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.
Суммой векторов является вектор Произведение Вектор Вектор
Определение:
Если
В связи с этим можно записать следующие свойства:
Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала. Если заданы точки А(x1, y1, z1), B(x2, y2, z2), то
Общее уравнение плоскости.
Плоскостью называется поверхность, вес точки которой удовлетворяют общему уравнению: Ax + By + Cz + D = 0, где А, В, С – координаты вектора
Кривые второго порядка.
Угол между плоскостями.
Таким образом, угол между плоскостями находится по формуле:
Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.
Полярная система координат.
Точка О называется полюсом, а луч l – полярной осью.
угол j называется полярным углом.
Тогда координаты произвольной точки в двух различных системах координат связываются соотношениями:
x = rcosj; y = rsinj;
Комплексные числа.
Комплексным числом z называется выражение
При этом число a называется действительной частью числа z (a = Re z), а b- мнимой частью (b = Im z).
Числа
Два комплексных числа
Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная ‑ мнимой осью.
С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.
Математический анализ.
Предел функции в точке.
Число А называется пределом функции f(x) при х®а, если для любого e>0 существует такое число D>0, что для всех х таких, что 0 < ïx - aï < D верно неравенство ïf(x) - Aï< e. То же определение может быть записано в другом виде: Если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e. Запись предела функции в точке:
Определение: Если f(x) ® A1 при х ® а только при x < a, то а если f(x) ® A2 при х ® а только при x > a, то
Пределы А1 и А2 называются также односторонними пределами функции f(x) в точке х=а.
Бесконечно малые функции.
Функция f(x) называется бесконечно малой при х®а, если
Свойства бесконечно малых функций:
Вычисление пределов. К разряду неопределенностей принято относить следующие соотношения:
При вычислении пределов необходимо избавиться от неопределенности.
Итого: Формулы сложения аргументов
Пример. Найти предел.
Пример. Найти предел.
Пример. Найти предел.
Пример. Найти предел.
Пример. Найти предел.
Пример. Найти предел Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби. x2 – 6x + 8 = 0; x2 – 8x + 12 = 0; D = 36 – 32 = 4; D = 64 – 48 = 16; x1 = (6 + 2)/2 = 4; x1 = (8 + 4)/2 = 6; x2 = (6 – 2)/2 = 2; x2 = (8 – 4)/2 = 2;
Пример. Найти предел.
=
Пример. Найти предел.
Пример. Найти предел
Разложим числитель и знаменатель на множители. x2 – 3x + 2 = (x – 1)(x – 2) x3 – 6x2 + 11x – 6 = (x – 1)(x – 2)(x – 3), т.к.
x2 – 5x + 6 = (x – 2)(x – 3) Тогда
Формула Тейлора.
Теорема Тейлора.
Тогда между точками х и а найдется такая точка e, что справедлива формула:
это выражение называется формулой Тейлора, а выражение:
называется остаточным членом в форме Лагранжа.
Формула Маклорена. Формулой Маклорена называется формула Тейлора при а = 0:
Правило Лопиталя.
Теорема (правило Лопиталя). Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g¢(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.
Пример: Найти предел Как видно, при попытке непосредственного вычисления предела получается неопределенность вида f¢(x) = 2x +
Пример: Найти предел
Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат.
Пример: Найти предел
Пример: Найти предел
Точки экстремума.
Точки максимума и минимума функции называются точками экстремума. Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х1 и точка х1 является точкой экстремума, то производная функции обращается в нуль в этой точке.
Следствие. Обратное утверждение неверно.
Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.
Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно.
Теорема. (Достаточные условия существования экстремума) Если при переходе через точку х1 слева направо производная функции f¢(x) меняет знак с “+” на “-“, то в точке х = х1 функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет минимум.
На основе вышесказанного можно выработать единый порядок действий при нахождении наибольшего и наименьшего значения функции на отрезке:
Асимптоты.
При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.
Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.
Вертикальные асимптоты: Из определения асимптоты следует, что если
Например, для функции
Наклонные асимптоты:
Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b.
Пример. Найти асимптоты и построить график функции
1) Вертикальные асимптоты: y®+¥ x®0-0: y®-¥ x®0+0, следовательно, х=0 вертикальная асимптота.
2) Наклонные асимптоты:
Таким образом, прямая у = х + 2 является наклонной асимптотой. Построим график функции:
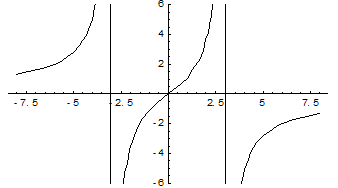
Пример. Найти асимптоты и построить график функции
Прямые х = 3 и х = -3 являются вертикальными асимптотами кривой.
Найдем наклонные асимптоты:
y = 0 – горизонтальная асимптота.
Пример. Найти асимптоты и построить график функции
Прямая х = -2 является вертикальной асимптотой кривой.
Найдем наклонные асимптоты.
Итого, прямая у = х – 4 является наклонной асимптотой.
Схема исследования функций
Процесс исследования функции состоит из нескольких этапов. Для наиболее полного представления о поведении функции и характере ее графика необходимо отыскать:
Пример. Исследовать функцию
Находим область существования функции. Очевидно, что областью определения функции является область (-¥; -1) È (-1; 1) È (1; ¥). В свою очередь, видно, что прямые х = 1, х = -1 являются вертикальными асимптотами кривой. Областью значений данной функции является интервал (-¥; ¥). Точками разрыва функции являются точки х = 1, х = -1. Находим критические точки. Найдем производную функции
Критические точки: x = 0; x = - Найдем вторую производную функции
Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках. Определим выпуклость и вогнутость кривой на промежутках.
Видно, что точка х = -
Про вертикальные асимптоты было уже сказано выше. Теперь найдем наклонные асимптоты.
Итого, уравнение наклонной асимптоты y = x. Построим график функции:
Основные действия над матрицами.
Если число столбцов матрицы равно числу строк (
Единичная матрица:
Диагональная матрица:
Если Суммой (разностью) матриц является матрица, элементами которой являются сумма (разность) соответствующих элементов исходных матриц:
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число. Пример. Даны матрицы А и B, найти 2А + В.
Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Пример. Найти произведение матриц
Матрицу
другими словами, Определители. Для матрицы первого порядка определителем является сам единственный элемент этой матрицы:
Для матрицы 2х2 определитель определяется как
Для матрицы nxn определитель задаётся формулой:
где Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:
Пример. Вычислить определитель матрицы
Или если вычислять по второй строке:
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.227.227 (0.014 с.) |

 ), то матрица называется квадратной.
), то матрица называется квадратной.

 , то матрица называется симметрической.
, то матрица называется симметрической. .
. .
.

 ,
, 
 ,
, 

 ,
,  .
. .
. называют транспонированной матрицей
называют транспонированной матрицей  , если элементы каждой строки матрицы
, если элементы каждой строки матрицы  ;
;  ;
; .
.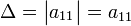

 ,
, – минор к элементу
– минор к элементу  . Он получается из исходной матрицы вычеркиванием первой строки и
. Он получается из исходной матрицы вычеркиванием первой строки и  -го столбца.
-го столбца. ,
, 
 .
.


 ;
;  ;
;  .
.


 ,
,  ,
, 
 .
. ;
;  ;
;  ;
; ;
;  ;
;  ;
; ;
;  ;
;  ;
;

 ,
,

 .
.



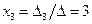 .
.
 ,
, ,
,  , где i = 2, 3, …, n; j = 2, 3, …, n+1.
, где i = 2, 3, …, n; j = 2, 3, …, n+1.

 , откуда получаем: x3 = 2; x2 = 5; x1 = 1.
, откуда получаем: x3 = 2; x2 = 5; x1 = 1.

 , при этом
, при этом 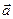 коллинеарен
коллинеарен  .
. - базис в пространстве и
- базис в пространстве и  , то числа a, b и g - называются компонентами или координатами вектора
, то числа a, b и g - называются компонентами или координатами вектора  =
=  .
. ;
;  ;
; .
. = (x2 – x1, y2 – y1, z2 – z1).
= (x2 – x1, y2 – y1, z2 – z1). -вектор нормали к плоскости.
-вектор нормали к плоскости. - уравнение эллипса.
- уравнение эллипса. - уравнение гиперболы.
- уравнение гиперболы. – уравнение параболы.
– уравнение параболы. – уравнение окружности радиуса
– уравнение окружности радиуса  с центром в точке
с центром в точке  .
.
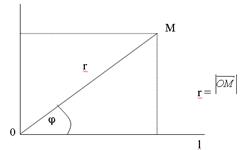

 , где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:
, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:
 называются комплексно-сопряженными.
называются комплексно-сопряженными. и
и  называются равными, если
называются равными, если 


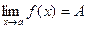
 - называется пределом функции f(x) в точке х = а слева,
- называется пределом функции f(x) в точке х = а слева, называется пределом функции f(x) в точке х = а справа.
называется пределом функции f(x) в точке х = а справа.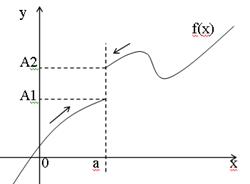
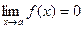 .
.
 , где
, где 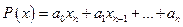 ,
,  - многочлены.
- многочлены.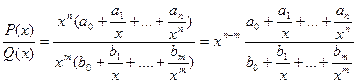

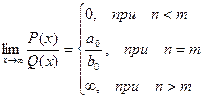
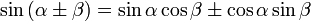


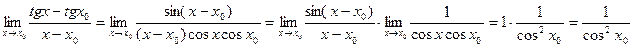



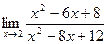 .
.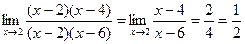
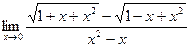 домножим числитель и знаменатель дроби на сопряженное выражение:
домножим числитель и знаменатель дроби на сопряженное выражение:  =
= .
.
 .
.
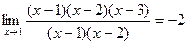





 .
. . Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.
. Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя. ; g¢(x) =
; g¢(x) =  ;
; ;
; .
. ;
;  ;
; .
. .
. ;
;  ;
; ;
;  ;
;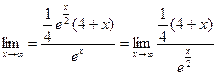
 ;
;  ;
; 
 .
. ;
;  ;
; - опять получилась неопределенность. Применим правило Лопиталя еще раз.
- опять получилась неопределенность. Применим правило Лопиталя еще раз. ;
;  ;
; - применяем правило Лопиталя еще раз.
- применяем правило Лопиталя еще раз. ;
;  ;
; ;
;
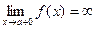 или
или 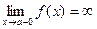 или
или  , то прямая х = а – асимптота кривой y = f(x).
, то прямая х = а – асимптота кривой y = f(x).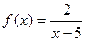 прямая х = 5 является вертикальной асимптотой.
прямая х = 5 является вертикальной асимптотой.
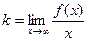 .
.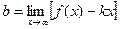
 .
.
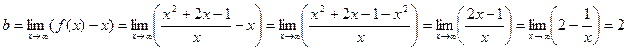

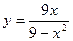 .
.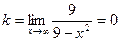
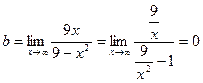
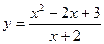 .
.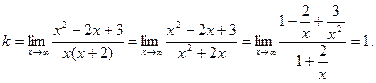

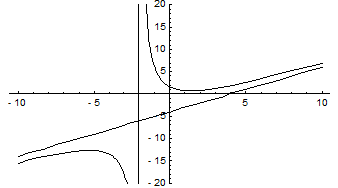
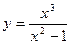 и построить ее график.
и построить ее график.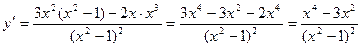
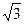 ; x =
; x = 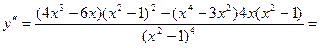

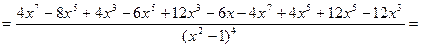
 .
.