
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение прямой в отрезках.
Геометрический смысл коэффициентов в том, что коэффициент
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
Угол между прямыми на плоскости.
Если заданы две прямые y = k1x + b1, y = k2x + b2, то острый угол между этими прямыми будет определяться как
Две прямые параллельны, если k1 = k2. Две прямые перпендикулярны, если k1 = -1/k2. Пример. Определить угол между прямыми: y = -3x + 7; y = 2x + 1. K1 = -3; k2 = 2 tgj = Расстояние от точки до прямой.
Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как
Кривые второго порядка.
Уравнение линии в пространстве.
Пусть F(x, y, z)=0 и Ф(x, y, z)=0 – уравнения поверхностей, пересекающихся по линии L. Тогда пара уравнений
называется уравнением линии в пространстве.
Угол между плоскостями.
Таким образом, угол между плоскостями находится по формуле:
Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.
Условия параллельности и перпендикулярности плоскостей.
плоскости перпендикулярны, если: Плоскости параллельны, если:
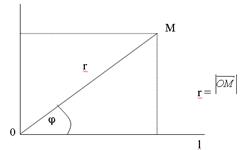
Полярная система координат.
Точка О называется полюсом, а луч l – полярной осью.
угол j называется полярным углом.
Тогда координаты произвольной точки в двух различных системах координат связываются соотношениями:
x = rcosj; y = rsinj;
Цилиндрическая и сферическая системы координат.
Если из точки М опустить перпендикуляр ММ1 на плоскость, то точка М1 будет иметь на плоскости полярные координаты (r, q).
Цилиндрическими координатами точки М называются числа (r, q, h), которые определяют положение точки М в пространстве.
Сферическими координатами точки М называются числа (r,j,q), где j - угол между r и нормалью.
Связь цилиндрической и декартовой прямоугольной системами координат: h = z; x = rcosq; y = rsinq;
cosq =
Связь сферической системы координат с декартовой прямоугольной:
Комплексные числа.
Комплексным числом z называется выражение
При этом число a называется действительной частью числа z (a = Re z), а b- мнимой частью (b = Im z).
Числа
Два комплексных числа
Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная ‑ мнимой осью.
С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.
Тригонометрическая форма числа.
Из геометрических соображений видно, что
При этом величина r называется модулем комплексного числа, а угол наклона j - аргументом комплексного числа.
Действия с комплексными числами.
Основные действия с комплексными числами вытекают из действий с многочленами.
В тригонометрической форме:
Таким образом, корень n-ой степени из комплексного числа имеет n различных значений.
Показательная форма комплексного числа.
Рассмотрим показательную функцию
Данное равенство называется уравнением Эйлера. Из него можно получить:
Математический анализ.
Числовая последовательность. Если каждому натуральному числу n поставлено в соответствие число
|
|||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.203 (0.014 с.) |
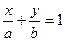 ,
, является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу. , а = -1, b = 1.
, а = -1, b = 1. .
. ; j = p/4.
; j = p/4. .
. - уравнение эллипса.
- уравнение эллипса. - уравнение гиперболы.
- уравнение гиперболы. – уравнение параболы.
– уравнение параболы. – уравнение окружности радиуса
– уравнение окружности радиуса  с центром в точке
с центром в точке  .
.

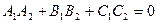 .
. .
.


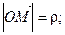 ОМ1 = r; MM1 = h;
ОМ1 = r; MM1 = h; ; sinq =
; sinq =  .
.

 , где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:
, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:
 называются комплексно-сопряженными.
называются комплексно-сопряженными. и
и  называются равными, если
называются равными, если 

 . Тогда комплексное число можно представить в виде:
. Тогда комплексное число можно представить в виде:





 ,
, 
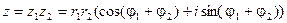




 ,
, 

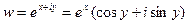

 , то говорят, что задана последовательность
, то говорят, что задана последовательность



