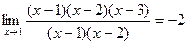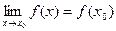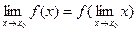Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ограниченные и неограниченные последовательности.Содержание книги
Поиск на нашем сайте
Последовательность {xn} называется ограниченной, если существует такое число М>0, что для любого n верно неравенство:
т.е. все члены последовательности принадлежат промежутку (-М; M).
Пример. {xn} = n – ограничена снизу {1, 2, 3, … }.
Число а называется пределом последовательности {xn}, если для любого положительного e>0 существует такой номер N, что для всех n > N выполняется условие:
Это записывается: lim xn = a.
В этом случае говорят, что последовательность {xn}сходится к
Теорема. Последовательность не может иметь более одного предела.
Возрастающие и убывающие последовательности называются строго монотонными.
Пример. {xn} = 1/n – убывающая и ограниченная {xn} = n – возрастающая и неограниченная.
Предел функции в точке.
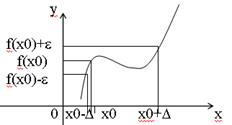
Число А называется пределом функции f(x) при х®а, если для любого e>0 существует такое число D>0, что для всех х таких, что 0 < ïx - aï < D верно неравенство ïf(x) - Aï< e. То же определение может быть записано в другом виде: Если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e. Запись предела функции в точке:
Определение: Если f(x) ® A1 при х ® а только при x < a, то а если f(x) ® A2 при х ® а только при x > a, то
Пределы А1 и А2 называются также односторонними пределами функции f(x) в точке х=а.
Предел функции при стремлении аргумента к бесконечности.
Определение. Число А называется пределом функции f(x) при х®¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство
Записывают:
Графически можно представить:
Основные теоремы о пределах.
Бесконечно малые функции.
Функция f(x) называется бесконечно малой при х®а, если
Свойства бесконечно малых функций:
Бесконечно большие функции и их связь с бесконечно малыми.
Функция называется бесконечно большой при х®а, если
Теорема. Если f(x)®0 при х®а (если х®¥) и не обращается в ноль, то
Если
Некоторые замечательные пределы.
Первый замечательный предел.
Второй замечательный предел
Кроме изложенных выше, пределов можно записать следующие полезные на практике соотношения:
Из замечательных пределов следует, что:
Пример. Найти предел Так как tg5x ~ 5x и sin7x ~ 7x при х ® 0, то, заменив функции эквивалентными бесконечно малыми, получим:
Вычисление пределов. К разряду неопределенностей принято относить следующие соотношения:
При вычислении пределов необходимо избавиться от неопределенности.
Итого: Формулы сложения аргументов
Пример. Найти предел.
Пример. Найти предел.
Пример. Найти предел.
Пример. Найти предел.
Пример. Найти предел.
Пример. Найти предел Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби. x2 – 6x + 8 = 0; x2 – 8x + 12 = 0; D = 36 – 32 = 4; D = 64 – 48 = 16; x1 = (6 + 2)/2 = 4; x1 = (8 + 4)/2 = 6; x2 = (6 – 2)/2 = 2; x2 = (8 – 4)/2 = 2;
Пример. Найти предел.
=
Пример. Найти предел.
Пример. Найти предел
Разложим числитель и знаменатель на множители. x2 – 3x + 2 = (x – 1)(x – 2) x3 – 6x2 + 11x – 6 = (x – 1)(x – 2)(x – 3), т.к.
x2 – 5x + 6 = (x – 2)(x – 3) Тогда
Непрерывность функции в точке.
Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.
Тот же факт можно записать иначе:
Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Пример непрерывной функции:
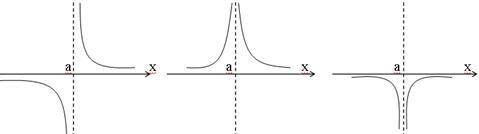
Пример разрывной функции:
|
||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 212; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.71.67 (0.01 с.) |

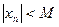

 при n®¥.
при n®¥.
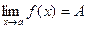
 - называется пределом функции f(x) в точке х = а слева,
- называется пределом функции f(x) в точке х = а слева, называется пределом функции f(x) в точке х = а справа.
называется пределом функции f(x) в точке х = а справа.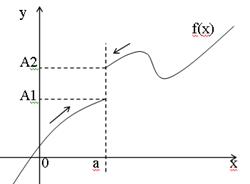

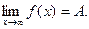

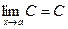 , где С = const.
, где С = const.
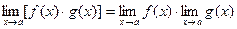
 при
при 
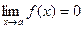 .
.

 то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.
то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.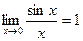

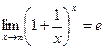




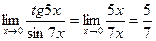

 , где
, где 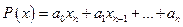 ,
,  - многочлены.
- многочлены.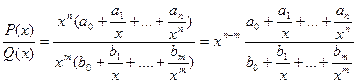

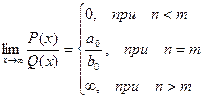
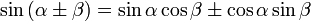


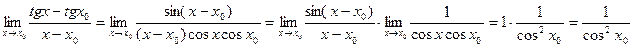



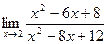 .
.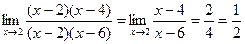
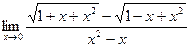 домножим числитель и знаменатель дроби на сопряженное выражение:
домножим числитель и знаменатель дроби на сопряженное выражение:  =
= .
.
 .
.