
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение производной функцииСодержание книги
Поиск на нашем сайте
Анализ формулировки определения производной: 1)число, 2)к которому стремится Δу/Δх, 3) при Δх→0. Механический смысл производной: V(to)=S’(to). Геометрический смысл производной: tg a= Δу/Δх= f’(xo).
Структура учебного материала 1)теорема о вычислении производных f’(xo)=0. 2)признаки возрастания и убывания ф-ции: f’(x)>0 – ф-ция возрастает, f’(x)<0 – ф-ция убывает. 3)точки экстремума(max,min). Необходимое условие – сущ производная в точке х0 равную 0. Достаточное условие – производная должна менять знак при переходе через х0. 4)наибольшее и наименьшее значение ф-ции на отрезке 5) наибольшее и наименьшее значение ф-ции на интервале 6)задачи на оптимизацию. Определение: Производной y ' =f ' (x) данной функции y=f(x) при данном x называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, если, конечно, этот предел существует, т.е. конечен. Возрастание и убывание функции. Экстремум функции. Определение 1. Функция f(x) называется возрастающей в интервале (a,b), если при возрастании аргумента x в этом интервале соответствующие значения функции f(x) также возрастают, т.е. если f(x2) > f(x1) при x2 > x1. Определение 2. Функция f (x) называется убывающей в интервале (a, b) если при возрастании аргумента x в этом интервале соответствующие значения функции f (x) убывают, т.е. если f(x2) < f(x1) при x2 > x1. 21. Проблемы методики изучения первых разделов систематического курса планиметрии С элементами геометрического материала учащиеся знакомятся еще в начальной школе: точка, линия (прямая, кривая), угол, отрезок, ломаная, круг и овал, различные многоугольники и их элементы (треугольник, прямоугольник, квадрат, трапеция), многогранники (куб, параллелепипед). Систематический курс геометрии В главе 2 учебного пособия Шлыкова начинается изложение систематического курса геометрии. В первых параграфах раскрывается сущность аксиоматического подхода к построению геометрической теории, состоящего в последующем изложении геометрических сведений, накопленных в обществе путем построения геометрических понятий из основных неопределяемых понятий и установление связей между ними при помощи утверждений, выражающих свойства геометрических фигур, аксиом, применяемых без доказательств и теорем, доказываемых путем логических утверждений. В учебнике геометрии Шлыкова вводят следующие аксиомы – характеризуют взаимное расположение прямой и точки. Аксиома 1. Каждой прямой принадлежит, по крайней мере, 2 точки. Аксиома 2. Существует, по крайней мере, 3 точки, принадлежащие одной прямой. Аксиома 3. Через любые 2 точки плоскости проходит единственная прямая, каждая точка которой принадлежит плоскости. Аксиома 4. Из 3-х точек на прямой единственная точка лежит между 2-мя другими. Аксиома 5. (отклад. отрезка) На любом луче от его начала можно отложить единственный отрезок, равный данному. Аксиома откладывания углов. От любого луча в данную полуплоскость можно отложить единственный угол, равный данному неразвёрнутому углу. Аксиоматический подход к построению теории требует строгости в определении понятий, формулировки аксиом и теорем, поэтому необходимо выучивать формулировки, введенных определений, аксиом и теорем. С различными геометрическими фигурами и их свойствами учащиеся знакомятся постепенно. Дети знакомятся с неопределяемыми понятиями: точка, прямая, плоскость. Главы 2 Определения: пересекающиеся и параллельные прямые. Теорема о единственности общей точки пересекающихся прямых. Символика × Направлен на формирование умений распознавать взаимное расположение точек и прямых по графическим моделям плоских и пространственных геометрических фигур, строить графические и символьные модели геом. конструкций, составленных из точек и прямых (под конструкцией понимается множество взаимосвязанных геометрических фигур). Основные задачи: 10, 11, 19, 21, 22, 25. Школьный курс планиметрии характеризуется линейно-концентрическим изложением материала, предполагающим как изложение конструкции, изуч. Геом. Фигур., так и изложение фактического материала. Главы 2 Понятия: отрезок, ломаная, луч, расстояние между точками, окружность, круг, а также связанные с ними понятия (движение ломаной, простые и замкнутые ломаные, противоположные лучи, равные отрезки:). Основная цель изучения отрезка, ломаной, окружности, а также связанные с ними понятия. 1 блок: закрепления отрезков, ломаной и …(34-46) 2 блок: окружность, длина ломаной, расстояние между точками. (47-57) 22. Методыка азначэння і вывучэння многавугольнікаў у куре планіметрыі. В уч. пособии В.В.Шлыкова Г9: «Многоугольником называется фигура, состоящая из точек простой замкнутой ломаной и точек ограниченной фигуры, для которой эта ломаная является границей».
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 406; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.14.104 (0.005 с.) |


 , или
, или 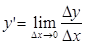
 ||. Задачи на материалы.
||. Задачи на материалы.


