
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика изучения площадей поверхностей многогранников в курсе средней школы.Содержание книги
Поиск на нашем сайте
Площади поверхностей многогранников изучаются в 11 кл. по мере изучения многогранников. Граница тела наз. его поверхностью. Площадью бок. поверхности призмы наз. сумма площадей ее боковых граней,
Т.(о площади бок. поверхности прямой призмы). Площадь бок. поверхности прямой призмы равна произведению периметра ее основания на высоту. (с док-ом). Площадь бок. поверхности наклонной призмы равна произведению периметра ортогонального сечения на длину ее бокового ребра.(дается в виде задачи с док-ом). Площадью бок. поверхности пирамиды наз. сумма площадей ее боковых граней,
Т. Площадь бок. поверхности правильной пирамиды равна половине произведения периметра основания на апофему. (с док-ом). Площадью бок. поверхности усеченной пирамиды наз. сумма площадей ее боковых граней, 30. Методыка вывучэння цел вярчэння. Аб’емы і плошчы паверхняў цел вярчэння. При изучении фигур вращения очень велико значение чертежа. Чертеж является основным средством иллюстрации, развития пространственного воображения. При этом необходимо помнить, что чертеж, который появляется на доске постепенно и сопровождается комментариями учителя, имеет большую педагогическую ценность. Учитель должен показать учащимся, не вдаваясь в подробности, как изобразить на плоскости фигуру вращения, то или иное её сечение. Для изображения каждого из изучаемых в школе тел вращения, их отдельных элементов, сечений необходимо напомнить учащимся об изображении окружности (учащиеся знакомы с этим из курса черчения). В школе изучаются конус, цилиндр, шар(сфера). Весь круг вопросов по теме «Тела вращения» можно условно разделить на две группы: 1) Цилиндр и конус: a) Определение, поверхность, симметрия, касательная плоскость, сечение осевое и перпендикулярное оси, вписанные и описанные многогранники; b) Объем; c) Площадь боковой поверхности. 2) Шар и сфера: a) Определение, симметрия, сечение, касательная плоскость; b) Объем шара; c) Площадь сферы. Обычно цилиндр, конус, шар и сфера изучаются в курсе стереометрии после многогранников. При этом такие понятия, как «тело», «поверхность», «ограниченность» и т.п., вводится в теме «Многогранники». Если цилиндр и конус изучаются по единой схеме, то шар (сфера) занимает особое место среди тел вращения. Именно при изучении шара и его поверхности наиболее полно используются знания учащихся о круге и окружности, полученные из курса планиметрии и других школьных дисциплин. В связи с этим основная роль учителя состоит в такой организации учебного процесса, когда ученики сами формулируют необходимые утверждения. В отличие от понятий цилиндра и конуса понятия шара и сферы трактуются как пространственные аналоги круга и окружности. Шар определяется как тело, состоящее из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. Сфера вводится как поверхность шара. Объемы тел вращения изучаются в 11 кл. по мере изучения тел за исключением шара (выносится в отдельный параграф). За объем цилиндра принимается число, к которому стремится объем правильной призмы, вписанной в цилиндр, когда число сторон ее основания неограниченно возрастает. Т.(об объеме цилиндра). Объем цилиндра равен произведению площади основания на высоту.( За объем конуса принимается число, к которому стремится объем правильной пирамиды, вписанной в конус, когда число сторон ее основания неограниченно возрастает. Т.(об объеме конуса). Объем конуса равен одной трети произведения площади основания на высоту.( Т. (об объеме шара). Объем шара c радиусом R вычисляется по формуле Площади поверхностей тел вращения изучаются в 11 кл. по мере изучения тел за исключением сферы (выносится в отдельный параграф). За площадь боковой поверхности цилиндра принимается число, к которому стремится площадь боковой поверхности правильной призмы, вписанной в цилиндр, когда число сторон оснований этой призмы неограниченно возрастает. Т.(о площади бок. поверхности цилиндра). Площадь бок. поверхности цилиндра равна произведению длины окружности его основания на высоту ( Площадью полной поверхности цилиндра наз. сумма площадей бок. поверхности и двух оснований цилиндра. Если бок. поверхность цилиндра «разрезать» по образующей и развернуть так, чтобы все образующие оказались в одной плоскости, то получим прямоугольник, который наз. разверткой бок. поверхности цилиндра. Площадь развертки=площади бок. поверхности. За площадь боковой поверхности конуса принимается число, к которому стремится площадь боковой поверхности, вписанной в конус правильной n-угольной пирамиды, когда число сторон основания пирамиды неограниченно возрастает. Т.(о площади бок. поверхности конуса). Площадь бок. поверхности конуса равна произведению половины длины окружности основания на образующую ( Площадью полной поверхности конуса наз. сумма площадей бок. поверхности и основания цилиндра. Если бок. поверхность конуса «разрезать» по образующей и развернуть так, чтобы все образующие оказались в одной плоскости, то получим круговой сектор, который наз. разверткой бок. поверхности конуса. Площадь развертки=площади бок. поверхности. В виде задачи дается формула для площади бок. поверхности усеченного конуса: Площадью полной поверхности усеченного конуса наз. сумма площадей его бок. поверхности и площадей основания Т.(о площади сферы). Площадь сферы равна За площадь части сферы, образованной поворотом какой-нибудь дуги полуокружности вокруг диаметра на 360, принимается число, к которому стремится площадь поверхности, образуемой поворотом вокруг того же диаметра правильной вписанной ломаной, когда ее звенья неограниченно уменьшаются. Для док-ства т. О площади сферы используется следующая теорема: Т. Пусть секущая плоскость перпендикулярна диаметру сферы радиуса R. Тогда площадь каждой из частей, на которые сфера разбивается секущей плоскостью, равна произведению длины большей окружности данной сферы на длину H соответствующего отрезка диаметра:
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1246; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.80.121 (0.009 с.) |

 . Площадью полной поверхности призмы наз. сумма всех ее граней,
. Площадью полной поверхности призмы наз. сумма всех ее граней, 
 .
. )
) )
)
 ).(с док-ом)
).(с док-ом) .
. ).(с док-ом)
).(с док-ом)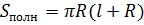 .
. .
. .
. .
. .
.


