
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика изучения перпендикулярности прямых и плоскостей в пространстве.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 10 кл. Две прямые называются взаимно перпендикулярными, если угол между ними равен 90. Если прямая Прямая, пересекающая плоскость, наз. перпендикулярной плоскости, если она перпендикулярна каждой прямой, лежащей в этой плоскости. Т1. Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая прямая перпендикулярна этой прямой. Т2. Если одна из двух параллельных прямых перпендикулярна плоскости, то другая прямая перпендикулярна этой плоскости Т3. Если две прямые перпендикулярны одной плоскости, то они параллельны. Т4. (признак перпенд. прямой и пл.). если прямая Т5. Через любую точку пространства проходит единственная плоскость, перпендикулярная данной прямой. Т6. Через любую точку пространства проходит единственная прямая, перпендикулярная данной плоскости. Т7. (о св-ве диагонали прямоугольного параллелепипеда). Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, имеющих общую вершину. Две плоскости наз. Перпендик-ыми, если угол между ними равен 90. Т.(признак Т2. Прямая, проведенная в одной из двух перпендикулярных плоскостей перпендиклярно прямой, по которой они пересекаются, перпендикулярна другой плоскости. (с док-ством). Двугранным углом наз. фигура, образованная двумя полуплоскостями с общей граничной прямой и частью пространства, для которой эти полуплоскости служат границей. Полуплоскости наз. гранями двугранного угла, общая граничная прямая – ребром. Линейным углом двугранного угла наз. угол, сторонами кот. Являются лучи с общим началом на ребре двугранного угла, которые проведены в его ранях перпендикулярно ребру. Градусной мерой двугранного ∠ наз. градусная мера его линейного ∠. Т.(признак Т2. Прямая, проведенная в одной из двух перпендикулярных плоскостей перпендиклярно прямой, по которой они пересекаются, перпендикулярна другой плоскости. (с док-ством). 28. Методыка навучання школьнікаў знаходжанню вуглоў і адлегласцей у прасторы. 1. Углом между скрещивающимися прямыми а и b называется угол между построенными пересекающимися прямыми а1 и b1, где а1 и b1 параллельные а и b соответственно. Для нахождения угла между двумя данными скрещивающимися прямыми а и b можно взять на одной из них, например на прямой а, некоторую точку О и в плоскости, определяемой прямой b и точкой О, провести прямую b1, параллельную прямой b. Тогда угол между прямыми а и b1, равен углу между скрещивающимися прямыми а и b. 2. Для нахождения угла между пересекающимися плоскостями α и β выбирают какую-нибудь точку С, принадлежащую линии с их пересечения, и восстанавливают перпендикуляры a и b к линии c, лежащие в плоскостях α и β соответственно. Угол между прямыми a и b будет искомым углом между плоскостями α и β. Если линия пересечения плоскостей α и β, указанных в задаче, не дана или находится вне данного рисунка, то для нахождения угла между плоскостями α и β выбирают какие-нибудь плоскости α’ и β’ соответственно параллельные α и β, линия пересечения которых расположена на рисунке. При этом одна из плоскостей α’ и β’ может совпадать соответственно с α или β. После этого находят угол между плоскостями α’ и β’. 1) Расстоянием от точки до плоскости наз. длина перпендикуляра, проведенного из этой точки к данной плоскости. Расстоянием между параллельными плоскостями наз. расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости. Расстоянием между прямой и параллельной ей плоскостью наз. расстояние от произвольной точки прямой до плоскости. Расстоянием между скрещивающимися прямыми наз. расстояние от одной из скрещивающихся прямых до плоскости, проходящей через другую прямую и параллельной первой прямой. Алгоритм построения расстояния между скрещивающимися прямыми: 1) Если есть две прямые a и b, нужно построить пл.α, такую что KO – искомое расстояние
2) Прямые расположены след. образом:

 , KO – искомое расстояние. , KO – искомое расстояние.
29. Методыка вывучэння мнагаграннікаў у курсе геаметрыі сярэдняй школы. Аб’емы і плошчы паверхняў мнагаграннікаў. 11 кл. Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два смежные из которых не лежат в одной плоскости; сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника. Геометрическим телом наз. ограниченная фигура в пространстве, обладающая следующими св-ами: 1)У нее есть внутренние точки, и любые две из них можно соединить ломаной, каждая точка которой является внутренней точкой фигуры.2)Фигура содержит свою границу, и е граница совпадает с границей внутренности. Многогранники бывают выпуклые и невыпуклые. Многогранник называется выпуклым, если он расположен по одну сторону от каждой из плоскостей, содержащих его грани. Призма (n-угольная) – это многогранник, у которого две грани – равные n-угольники (называемые основаниями), а остальные n граней – параллелограммы, у каждого из которых две стороны явл. соответственными сторонами оснований. Эти остальные параллелограммы – боковые грани призмы, а их стороны, не явл. сторонами оснований призмы, наз. боковыми ребрами призмы. Фигура образованная всеми гранями призмы, наз. полной поверхностью призмы, а фигура, образованная бок. гранями, - боковой поверхностью призмы. Высотой призмы наз. перпендикуляр, проведенный из какой-нибудь точки плоскости одного основания к плоскости другого основания. Прямая призма – это такая призма, у которой боковые грани – прямоугольники. Призма, не явл. прямой призмой, наз. наклонной. Правильная n-угольная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильные n-угольники. Диагональю призмы наз. отрезок, концами кот. Служат вершины призмы, не лежащие в одной грани. Диагональным сечением призмы наз. ее сечение плоскостью, проходящей через два боковых ребра, кот. не лежат в одной грани. Если секущая плоскость пересекает все боковые ребра призмы и перпендикулярна им, то получающееся при этом сечение наз. ортогональным сечением призмы. Параллелепипед – это призма, основаниями кот. являются параллелограммы. 2 грани параллелепипеда, не имеющие общего ребра, наз. противолежащими, а имеющие общее ребро, - смежными. 2 вершины, не принадлежащие одной грани, наз. противолежащими. Отрезок, соединяющий противолежащие вершины, наз. диагональю параллелепипеда. Параллелепипед, все бок. грани кот. – прямоугольники, наз. прямым. Если параллелепипед не явл. прямым, то он наз. наклонным. Параллелепипед наз. прямоугольным, если все его грани – прямоугольники. Длины трех ребер, выходящих из одной вершины, наз. измерениями прямоугольного параллелепипеда. Методика изучения объёмов многогранников в курсе средней школы. Объемы многогранников изучаются в 11 кл. в отдельной главе. Понятие объема вводится аналогично понятию площади через систему св-в. Объем – это положительная величина, определенная для каждого из рассматриваемых тел, числовое значение которой имеет св-ва: 1) Равные геометрические тела имеют равные объемы; 2) Если геометрическое тело есть объединение тел, не имеющих общих внутренних точек, то его объем равен сумме объемов тел, его составляющих; 3) Объем куба, ребро которого равно 1 измерения длины, равен 1. Каждый многогранник имеет объем, который измеряется с помощью выбранной единицы объема. Т. (об объеме прямоугольного параллелепипеда). Объем прямоугольного параллелепипеда равен произведению трех его измерений, т.е. Следствие. Объем прямоугольного параллелепипеда равен произведению площади его основания на высоту. Т. (об объеме прямого параллелепипеда). Объем прямого параллелепипеда равен произведению площади его основания на высоту. (с док-ом). Т. (об объеме наклонного параллелепипеда). Объем наклонного параллелепипеда равен произведению площади основания на высоту параллелепипеда. (с док-ом). Т. (об объеме призмы). Объем призмы равен произведению площади основания на высоту. (с док-ом). Следствие. Объем прямой призмы равен произведению площади основания на длину бокового ребра. Т. Две треугольные пирамиды, имеющие равные высоты и равные площади оснований, имеют равные объемы. (с док-ом). Т. (об объеме пирамиды). Объем любой треугольной пирамиды равен одной третьей произведения площади ее основания на высоту. (с док-ом). Т. (об объеме n-угольной пирамиды). Объем n-угольной пирамиды равен одной третьей произведения площади ее основания на высоту. (с док-ом).
|
||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 956; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 перпендикулярна прямой
перпендикулярна прямой  , то пишут
, то пишут  .
. .
. двум пересекающимся прямым, лежащим в плоскости, то она
двум пересекающимся прямым, лежащим в плоскости, то она 
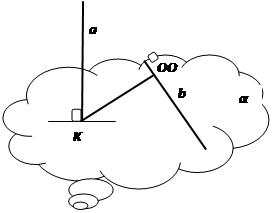

 - построить проекцию
- построить проекцию 


 . (с док-ом).
. (с док-ом).


