
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимное расположение плоскостей. Пучок плоскостейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1 Установить взаимное расположение следующих пар плоскостей: а) в) 2 Составить уравнение плоскости, проходящей через начало координат и параллельной плоскости а) 3 Составить уравнение плоскости, проходящей через точку М (1; -3; 5) и параллельной плоскости: а) 4 Плоскость в прямоугольной декартовой системе координат задана уравнением 5 Через линию пересечения плоскостей а) проходящую через начало координат; б) проходящую через точку А (1; 1; 1); в) параллельную оси Оу. 6 В пучке, определяемом плоскостями М (1; 0; 1). 7 Определить двугранные углы между следующими парами плоскостей: а) б) 8 Определить, при каких значениях а) б) в) 9 Определить, при каком значении а) б) в)
Расстояние от точки до плоскости. Геометрический смысл знака многочлена 1 Даны точки и плоскости: а) б) Для каждой из данных плоскостей среди указанных точек выбрать те, которые лежат по ту же сторону от плоскости, что и начало координат. 2 Дана плоскость а) О (0; 0; 0) и А (2; 1; 0); б) 3 Две пересекающиеся плоскости 4 Привести к нормальному виду уравнения плоскостей: а) д) 5 Найти расстояние от точки до плоскости в каждом из следующих случаев: а) б) 6 Установить расположение плоскости а) в) 7 Вычислить расстояние между следующими парами параллельных плоскостей: а) б) в) 8 На оси Оz найти точку, равноудаленную от точки М (1; 1; 4) и от плоскости 9 Составить уравнения множества точек, отстоящих от плоскости 10 Составить уравнения множества точек, равноудаленных от двух параллельных плоскостей в каждом из следующих случаев: а) б) 11 Написать уравнение плоскостей, делящих пополам двугранные углы между плоскостями: а) б) 12 Доказать, что плоскость 13 Две грани куба лежат на плоскостях 14 Определить, лежит ли начало координат внутри острого или тупого угла, образованного двумя плоскостями 15 Составить уравнение плоскости, делящей пополам тот двугранный угол между двумя плоскостями 16 Составить уравнение плоскости, делящей пополам тот двугранный угол между двумя плоскостями 17 Составить уравнение плоскости, которая делит пополам острый двугранный угол, образованный двумя плоскостями 18 Составить уравнение плоскости, которая делит пополам тупой двугранный угол, образованный двумя плоскостями
Имеет место утверждение: Пусть плоскости
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 756; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.72.181 (0.007 с.) |

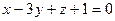 ,
,  ; б)
; б) 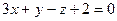 ,
,  ;
; ,
, 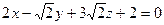 ; г)
; г) 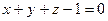 ,
, 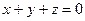 .
. ; б)
; б) 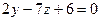 ; в)
; в) 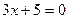 .
. ; б)
; б)  ; в)
; в) 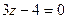 .
.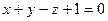 . Написать уравнение плоскости, проходящей через линию пересечения данной плоскости и плоскости Оxz и перпендикулярной плоскости
. Написать уравнение плоскости, проходящей через линию пересечения данной плоскости и плоскости Оxz и перпендикулярной плоскости 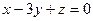 .
. ,
, 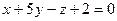 провести плоскость:
провести плоскость: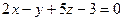 и
и  найти две перпендикулярные плоскости, одна из которых проходит через точку
найти две перпендикулярные плоскости, одна из которых проходит через точку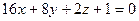 ,
, 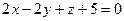 ;
;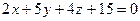 ,
,  .
. и
и 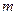 следующие пары уравнений будут определять параллельные плоскости:
следующие пары уравнений будут определять параллельные плоскости: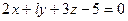 ,
, 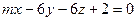 ;
;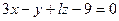 ,
, 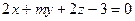 ;
; ,
,  .
.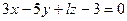 ,
,  ;
; ,
, 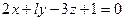 ;
; ,
,  .
.
 ,
, 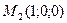 ,
, 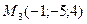 ,
, 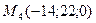 ,
, 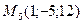 ,
, 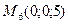
 ;
;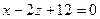 .
. . Указать, какие из пар точек, приведенных ниже, лежат по одну и ту же сторону от данной плоскости:
. Указать, какие из пар точек, приведенных ниже, лежат по одну и ту же сторону от данной плоскости: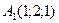 И
И 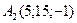 ; В)
; В)  И
И 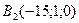 .
.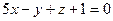 и
и 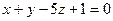 делят множество точек пространства, не лежащих на них, на четыре двугранных угла (области). Составить систему неравенств, определяющих внутреннюю область двугранного угла, которому принадлежит точка М (3; 1; 2).
делят множество точек пространства, не лежащих на них, на четыре двугранных угла (области). Составить систему неравенств, определяющих внутреннюю область двугранного угла, которому принадлежит точка М (3; 1; 2).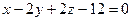 ; б)
; б)  ; в)
; в) 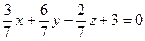 ; г)
; г) 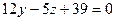 ;
;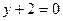 ; е)
; е)  .
.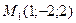 ,
,  ;
;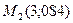 ,
, 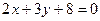 .
.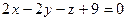 относительно сферы в каждом из следующих случаев:
относительно сферы в каждом из следующих случаев: ; б)
; б) 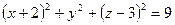 ;
;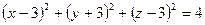 ; г)
; г) 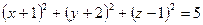 .
.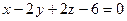 ;
;  ;
; ;
;  ;
; ;
; 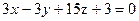 .
. .
.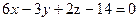 на расстоянии, равном 3.
на расстоянии, равном 3. и
и 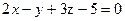 ;
;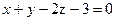 и
и  .
. и
и  ;
; и
и 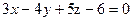 .
.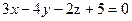 пересекает отрезок, ограниченный точками
пересекает отрезок, ограниченный точками 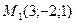 и
и 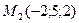 .
.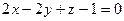 и
и  . Вычислить объем этого куба.
. Вычислить объем этого куба. ,
, 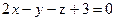 .
. ,
,  , в котором лежит начало координат.
, в котором лежит начало координат.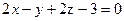 ,
, 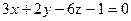 , в котором лежит точка М (1; 2; -3).
, в котором лежит точка М (1; 2; -3).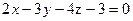 и
и  .
.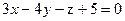 ,
, 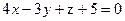 .
.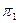 и
и  , заданные в прямоугольной декартовой системе координат уравнениям
, заданные в прямоугольной декартовой системе координат уравнениям 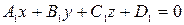 ,
, 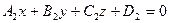 , пересекаются, но не перпендикулярны друг другу. Тогда внутренние области двух вертикальных двугранных острых углов, образованных этими плоскостями, характеризуются неравенством
, пересекаются, но не перпендикулярны друг другу. Тогда внутренние области двух вертикальных двугранных острых углов, образованных этими плоскостями, характеризуются неравенством 
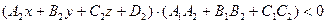 , а внутренние области двух вертикальных двугранных тупых углов - неравенством
, а внутренние области двух вертикальных двугранных тупых углов - неравенством  .
.


