
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3 прямая линия на плоскостиСодержание книги
Поиск на нашем сайте
Теоретические вопросы 1 Какими способами может быть задана на плоскости прямая? Обосновать каждый способ. 2 Какие векторы называются направляющим и нормальным векторами прямой? Сколько направляющих (нормальных) векторов имеет прямая? 3 Какое уравнение прямой называется общим уравнением? Как находятся координаты направляющего и нормального векторов из общего уравнения прямой? Каков геометрический смысл коэффициентов в общем уравнении прямой? 4 Написать уравнения прямой: а) по точке и направляющему вектору (параметрические, каноническое); б) по двум точкам; уравнение прямой «в отрезках»; в) уравнение прямой с угловым коэффициентом. В чем заключается геометрический смысл углового коэффициента? г) уравнение прямой, заданной точкой и нормальным вектором. 5 Как могут располагаться две прямые на плоскости? 6 Сформулируйте аналитические условия взаимного расположения двух прямых, если прямые заданы: а) общими уравнениями; б) уравнениями с угловыми коэффициентами. 7 Как вычислить угол между прямыми, заданными общими уравнениями? 8 Как вычислить угол между прямыми, заданными уравнениями с угловыми коэффициентами? 9 Сформулировать определение и записать уравнение: а) пучка пересекающихся прямых; б) пучка параллельных прямых. 10 Как находится расстояние: а) от точки до прямой; б) между двумя параллельными прямыми? 11 Какой вид имеет нормальное уравнение прямой? Что нужно знать, чтобы его составить? 12 Как общее уравнение прямой привести к нормальному виду? 13 В чем заключается геометрический смысл знака многочлена 14 Каковы условия того, что точки
Задачи
Способы задания прямой. Уравнения прямой 1 Написать уравнение прямой: а) проходящей через точки А (-1; 1) и В (2; 5); б) проходящей через точку А (2; -6) и параллельной вектору в) отсекающей на осях координат отрезки а = 3, b = -2; г) проходящей через точку В (-1; 2) и параллельной оси Оу; д) проходящей через точку А (3; 5) и параллельной оси Ох; е) проходящей через точку А (2; 2) и параллельной прямой 2 Составить уравнение прямой АВ, если А (5; -3), В (-1; -2). 3 Дан треугольник АВС: А (0; 0), В (0; 2), С (-4; 0). Составить уравнения прямых, содержащих стороны треугольника АВС. 4 Найти точки пересечения с осями координат прямой, заданной уравнением: 5 Найти точку пересечения прямых, заданных уравнениями: 6 Составить уравнение прямой, параллельной оси х и проходящей через точку (2; 3); параллельной оси у и проходящей через точку (2; -3); проходящей через начало координат и точку (2; 3). 7 Доказать, что три прямые
8 Найти координаты точки пересечения медиан (центроид) треугольника с вершинами А (1; 0), В (2; 3), С (3; 2). 9 Среди прямых, заданных уравнениями, указать пары параллельных прямых: 1) 2) 3) 10 Найти угловые коэффициенты прямых, заданных уравнениями: 1) 2) 11 Найти острые углы, которые образует заданная прямая с осью Ох: а) 12 Найти точки пересечения окружности 13 В треугольнике АВС: А (-1; 3), В (0; 4), С (-2; -2). Написать уравнение медианы треугольника, проведенной из вершины А. 14 В треугольнике АВС: А (2; 6), В (-4; 0), С (4; 2). Написать уравнение средних линий треугольника. 15 Установить, какие из следующих троек точек лежат на одной прямой: а) (2; 1), (-1; 4), (-7; 10); в) (1; 0), (0; 1), (-2; 3); б) (0; 5), (7; 1), (-2; 3); г) (2; 1), (10; 3), (5; 2). 16 Найти длины направленных отрезков, отсекаемых на осях координат прямыми: а) б) в) Составить уравнения этих прямых в отрезках. 17 Прямая задана параметрическими уравнениями а) найти направляющий вектор данной прямой; б) определить координаты точек, имеющих параметры: в) определить параметры точек пересечения данной прямой с осями координат; г cреди точек 18 Даны прямые: а) 19 Записать общие уравнения следующих прямых, заданных параметрически: а) 20 Даны середины сторон треугольника М (2; -1), N (-3; 3) и Р (-1; 0). Составить уравнения его сторон. 21 Дана прямая а) координаты направляющего вектора б) координаты нормального вектора в) угловой коэффициент г) отрезки а и b, отсекаемые на осях координат данной прямой. 22 Написать уравнение прямой: а) проходящей через точку А (-1; 3) и перпендикулярной к вектору б) проходящей через точку В (5; 10) и перпендикулярной к прямой в) проходящей через начало координат и перпендикулярной к прямой 23 Написать уравнение прямой, проходящей через точку Р (1; 2) и отсекающей равные отрезки на осях координат. 24 Вершины треугольника находятся в точках А (-4; -5), В (4; 1) и а) биссектрисы внутреннего угла А; б) высоты, опущенной из вершины С. 25 Вычислить площадь треугольника, отсекаемого прямой 26 Составить уравнение прямой, которая проходит через точку С (1; 1) и отсекает от координатного угла треугольник с площадью, равной 2.
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.181.69 (0.006 с.) |

 ?
?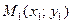 и
и 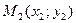 лежат по одну (по разные) сторону от прямой
лежат по одну (по разные) сторону от прямой  ?
? ;
; .
. .
. .
. ,
,  и
и  пересекаются в одной точке.
пересекаются в одной точке. ; 4) у = 4;
; 4) у = 4; ; 5)
; 5) 
 ; 6)
; 6)  .
. ;
; ; 4)
; 4)  .
. ; б)
; б)  ; в)
; в)  .
. с прямой
с прямой  .
. ;
; .
. ,
, 
 ,
,  ,
,  ,
,  ;
; ,
,  ,
,  ,
,  ,
,  найти точки, принадлежащие данной прямой.
найти точки, принадлежащие данной прямой.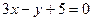 ; б)
; б)  ; в)
; в)  . Написать уравнение каждой из них в параметрическом виде.
. Написать уравнение каждой из них в параметрическом виде. ,
,  ; б)
; б)  ,
,  ; в)
; в)  ,
,  .
. . Определить:
. Определить: ;
;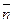 ;
; ;
;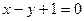 ;
; .
. . Написать уравнения:
. Написать уравнения: от координатного угла.
от координатного угла.


