
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимное расположение двух прямых. Пучки прямых. Угол между прямымиСодержание книги
Поиск на нашем сайте
1 Составить уравнение прямой, симметричной данной прямой 2 Даны пары прямых: а) б) в) г) д) Выяснить, какие из данных пар прямых взаимно перпендикулярны. 3 В пучке 4 В пучке 5 Через точку пересечения прямых 7 На плоскости проведена прямая так, что точка А (1; 2) является серединой ее отрезка, заключенного между осями координат. Написать уравнение этой прямой. 8 При каком значении параметра t прямые, заданные уравнениями 9 Составить уравнение множества точек, равноудаленных от двух параллельных прямых: а) б) 10 Найти угол, образованный двумя прямыми, заданными в определенном порядке своими уравнениями в каждом из следующих случаев (предполагается, что плоскость ориентирована при помощи системы координат): а) в) 11 Через точку (-1; 5) провести прямые, наклоненные к прямой 11 Даны уравнения сторон треугольника АВ: АС: 12 Доказать, что прямые 13 Установить, какие из следующих пар прямых перпендикулярны: 1) 3) 5) Решить задачу, не вычисляя угловых коэффициентов данных прямых. 14 Определить, при каких значениях m и n две прямые а) параллельны; б) совпадают; в) перпендикулярны. 15 Определить, при каком значении m две прямые 16 Определить, при каких значениях а и b две прямые а) имеют одну общую точку; б) параллельны; в) совпадают.
Расстояние от точки до прямой. Геометрический смысл знака многочлена 1 Найти проекцию точки Р (-6; 4) на прямую 2 Найти точку Q, симметричную точке Р (-5; 13) относительно прямой 3 Даны вершины треугольника А (1; -2), В (5; 4), С (-2; 0). Составить уравнение биссектрис его внутреннего и внешнего углов при вершине А. 4 Две стороны квадрата лежат на прямых 5 Составить уравнение биссектрисы того угла между прямыми 6 На оси Ох найти точку, равноудаленную от прямых 7 Найти расстояние от точки до прямой в каждом из следующих случаев: а)
в) 8 Найти расстояние от точек А (1; 2), В (-1; 3), С (1; 6) до прямой 9 Найти длины высот треугольника, стороны которого заданы уравнениями 10 Через точку М (-1; 4) проведена прямая, расстояние которой до точки Q (-2; -1) равно 5. Составить ее уравнение. 11 В каждом из следующих случаев найти уравнение биссектрис углов, образованных прямыми: а) б) 12 Составить уравнение биссектрисы тупого угла, образованного прямыми 13 Составить уравнение окружностей, касающихся двух данных прямых 14 Составить уравнение биссектрисы того угла между прямыми 15 Дана прямая а) б) в) 16 Найти проекцию точки М, заданной своими координатами, на прямую l, заданную своим уравнением М(5; -2),
Имеет место утверждение: Пусть прямые
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.233.156 (0.01 с.) |

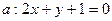 , относительно точки А (2; 3).
, относительно точки А (2; 3).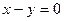 и
и  ;
; и
и  ;
; и
и  ;
; и
и  ;
; и
и  найти прямую, параллельную прямой
найти прямую, параллельную прямой  .
. найти прямую, проходящую через начало координат.
найти прямую, проходящую через начало координат. ,
,  проведена прямая, перпендикулярная к прямой
проведена прямая, перпендикулярная к прямой  . Написать уравнение этой прямой.
. Написать уравнение этой прямой. и
и  , параллельны?
, параллельны?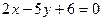 ;
; 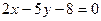 ;
; ;
;  .
. ;
;  ; б)
; б)  ;
;  ;
; ;
;  .
.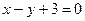 под углом, тангенс которого равен: а)
под углом, тангенс которого равен: а)  ; б)
; б)  .
. , ВС:
, ВС:  ,
,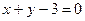 . Определить тангенсы его внутренних углов.
. Определить тангенсы его внутренних углов. не проходят через одну точку:
не проходят через одну точку:  .Найти уравнение прямой, проходящей через точку А =
.Найти уравнение прямой, проходящей через точку А =  параллельной прямой
параллельной прямой  .
. ,
,  ; 2)
; 2)  ,
,  ;
; ,
,  ; 4)
; 4)  ,
,  ;
; ,
,  ; 6)
; 6)  ,
,  .
. :
: пересекаются в точке, лежащей на оси абсцисс.
пересекаются в точке, лежащей на оси абсцисс. :
:
 .
. .
. ,
, 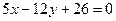 . Вычислить его площадь.
. Вычислить его площадь. ,
, 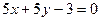 , в котором лежит начало координат.
, в котором лежит начало координат. ,
,  .
. ,
,  ; б)
; б)  ,
, 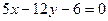 ;
; ,
, 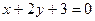 .
. ,
,  ,
,  .
. и
и  ;
; и
и  .
. и
и  .
. и
и  и имеющих радиус, равный 5.
и имеющих радиус, равный 5. и
и  , в котором лежит точка М (1; 2).
, в котором лежит точка М (1; 2). . Указать, какие из пар точек, приведенных ниже, лежат по разные стороны от данной прямой:
. Указать, какие из пар точек, приведенных ниже, лежат по разные стороны от данной прямой: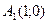 и
и  ;
; и
и  ;
; и
и 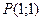 .
. .
. , заданные в прямоугольной декартовой системе координат уравнениями
, заданные в прямоугольной декартовой системе координат уравнениями 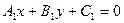 ,
,  , пересекаются, но не перпендикулярны друг другу. Тогда внутренние области двух вертикальных острых углов, образованных этими прямыми, характеризуются неравенством
, пересекаются, но не перпендикулярны друг другу. Тогда внутренние области двух вертикальных острых углов, образованных этими прямыми, характеризуются неравенством 
 , а внутренние области двух вертикальных тупых углов неравенством
, а внутренние области двух вертикальных тупых углов неравенством  .
.


