
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейчатые поверхности. Прямолинейные образующиеСодержание книги
Поиск на нашем сайте
1 Изобразить цилиндрические поверхности, заданные уравнением: а) 2 Исследовать поверхность второго порядка, заданную в прямоугольной декартовой системе координат уравнением: а) 3 Составить уравнение поверхности, образованной вращением параболы
4 В плоскости XOZ дана окружность с центром в точке (4; 0; 0) радиуса 5 Написать уравнения следующих поверхностей вращения: а) получающейся при вращении эллипса б) получающейся при вращении гиперболы 6 Написать уравнения двух систем прямолинейных, образующих однополостного гиперболоида 7 На гиперболическом параболоиде
8 Найти прямолинейные, образующие гиперболоида, заданного уравнением 9 Найти те прямолинейные образующие гиперболического параболоида 10 Найти прямолинейные образующие однополостного гиперболоида 11 Найти прямолинейные образующие гиперболического параболоида Тема 6. Геометрические преобразования на плоскости
Теоретические вопросы
1Определение движения, основная теорема и свойства. Классификация движений. 2 Виды движений: осевая симметрия, параллельный перенос, центральная симметрия, поворот. Определения, способы задания и построение образов точек, свойства. 3 Сущность метода геометрических преобразований при решении задач на доказательство, построение, вычисление. 4 Преобразования плоскости: гомотетия и подобие. Определения, способы задания и построение образов точек, свойства. 5 Аффинные преобразования: определение, основные свойства, примеры. Задачи Метод движений а) задачи на доказательства 1 На высоте ВД треугольника АСВ взята точка К так, что АК = КС. Доказать, что треугольник АВС равнобедренный. 2 Построить квадрат, две противоположные вершины которого лежали бы на данной прямой, а две другие – на данных окружностях. 3 На стороне АВ параллелограмма АВСД, вне его, построен квадрат АВМК, а на стороне СД в той же полуплоскости, что и параллелограмм, построен квадрат СДРЕ. Доказать, что расстояние между центрами квадратов равно стороне параллелограмма. 4 Две прямые, содержащие точку пересечения диагоналей параллелограмма, пересекают его стороны соответственно в точках М и К, Р и Е. Доказать, что МРКЕ – параллелограмм. 5 Две равные окружности пересекаются в точках А и В. Через Точку А проведена хорда МА одной окружности, а через точку В – хорда ВК другой окружности, причем МА и ВК параллельны. Доказать, что эти хорды равны. 6 Дан правильный шестиугольник ABCDEF, М – середина диагонали АС, N – середина стороны DE. Доказать, что треугольник MNF – правильный. 7 Через центр правильного треугольника проведены две прямые, угол между которыми равен 600. Доказать, что отрезки этих прямых, которые являются их пересечением с треугольником, равны. б) задачи на построение и вычисление 1 На данной прямой построить такую точку, чтобы сумма расстояний от этой точки до двух данных точек, не лежащих на этой прямой, была наименьшей. 2 Найти площадь трапеции, сумма оснований которой равна 21 см, а диагонали равны 13 см и 20 см. 3Даны две пересекающиеся прямые c и d и две точки А и В, не принадлежащие им. Построить параллелограмм АВСД так, чтобы вершины С и Д лежали соответственно на прямых c и d. 4 Построить биссектрису угла АОВ, вершина О которого не доступна. 5 Земельный участок квадратной формы был огорожен. От изгороди сохранились два столба на параллельных сторонах квадрата. Кроме того остался столб в центре участка. Построить границу участка. 6 Построить параллельные прямые а, b, с, проходящие соответственно через данные точки А, В, С так, чтобы одна из них была средней линией полосы, определяемой двумя другими прямыми. 7 Построить равнобедренный прямоугольный треугольник так, чтобы вершины его острых углов принадлежали данным окружностям, а вершиной прямого угла являлась данная точка. 8 На сторонах АВ и АС треугольника АВС, вне его построены квадраты ABMN и ACPQ. Найти длину отрезка NQ, если длина медианы АЕ треугольника АВС равна m. Метод преобразований 1 Доказать, что точка пересечения прямых, содержащих боковые стороны равнобедренной трапеции, точка пересечения ее диагоналей и середины оснований трапеции принадлежат одной прямой. 2 Через точку касания двух окружностей проведены две произвольные прямые, которые пересекают эти окружности в точках А, В и С, Д, причем А и В лежат на одной окружности, С и Д – на другой. Доказать, что АВ ׀׀ СД. 3 Даны две окружности и точка М. Построить на окружностях соответственно точки А и В, чтобы М Î АВ и АМ: МВ = 2: 3. 4 Построить равнобедренный треугольник, зная угол при его вершине и сумму длин основания и высоты. 5 Доказать, что отношение площади данного четырехугольника к площади четырехугольника, вершины которого находятся в серединах сторон данного, равно 2: 1. 6 Пользуясь только одной линейкой: а) построить середину отрезка, лежащего на одной из двух данных параллельных прямых; б) построить прямую, проходящую через данную точку М и параллельную двум данным параллельным прямым, не содержащим точку М.
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.148 (0.007 с.) |

 ; б)
; б)  ; в)
; в)  .
.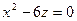 ; б)
; б) 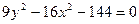 .
. ,
,  вокруг оси OZ.
вокруг оси OZ. . Написать уравнение поверхности вращения, образованной вращением данной окружности вокруг оси OZ.
. Написать уравнение поверхности вращения, образованной вращением данной окружности вокруг оси OZ.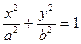
 ,
, 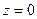 вокруг большой (малой) оси;
вокруг большой (малой) оси; ,
,  , и определить те из них, которые проходят через точку М (3;
, и определить те из них, которые проходят через точку М (3;  ; -1).
; -1). найти прямолинейные образующие, параллельные плоскости
найти прямолинейные образующие, параллельные плоскости  .
. , проходящие через точку А (6; 2; 8).
, проходящие через точку А (6; 2; 8). , которые образуют с прямой
, которые образуют с прямой  угол 45º.
угол 45º. , параллельные плоскости
, параллельные плоскости  .
.


