Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аффинная и прямоугольная декартова система координат на плоскости. Основные задачи на координатыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1 В прямоугольной декартовой и аффинной системах координат построить следующие точки: А (- 1; 0), В (- 2; 1), С (1; 1), D (- 3; 2), E (0; - 2), F (- 3; 3). 2 Построить точки А (- 2; 3; 4;) и В (2; - 3; - 2) в прямоугольной декартовой и в аффинной системах координат. 3 В аффинной системе координат даны координаты вектора а) 4 Начало координат помещено в центре квадрата, сторона которого равна 2 а. Найти координаты вершин квадрата, если: а) стороны квадрата параллельны осям координат; б) диагонали квадрата лежат на осях координат. 5 Вершины четырехугольника находятся в точках А (1; - 3), В (8; 0), С (4; 8) и D (- 3; 5). Доказать, что ABCD – параллелограмм. 6 Вершины четырехугольника находятся в точках А (1; 1), В (2; 3), С (5; 0) и D (7; - 5). Доказать, что ABCD – трапеция. 7 Даны три вершины параллелограмма: А (- 1; 3), В (2; - 5), С (0; 4). Определить четвертую вершину D, противоположную В. 8 Даны две вершины равностороннего треугольника А (- 3; 2), В (1; 4). Найти третью вершину С. 9 Даны две смежные вершины параллелограмма А (- 4; 4), В (2; 8) и точка М (2; 2) пересечения его диагоналей. Определить две другие вершины С и D. 10 Опеделить координаты точек, делящих отрезок А (2; 3), В (-1;2) в отношении 11 Доказать, что в аффинной системе координат точка М (х; у) пересечения медиан треугольника с вершинами а) А (3; 1), В (-1; 4), С (1; 1); б) А (-2; 3), В (5; -2), С (-3; -1).
12 Даны координаты вершин треугольника АВС: А (5; -4), В (-1; 2), С (5; 1). Найти длину медианы АМ. 13 Даны координаты вершин треугольника АВС: А (4; 1), В (7; 5), С (-4; 7). Вычислить длину биссектрисы AD угла А. 14 Доказать, что треугольник АВС – прямоугольный, если А (1; 1), В (2; 5), С (-6; 7). Указать вершину прямого угла (применить обратную теорему Пифагора). 15 На оси абсцисс айти точку, равноудаленную от точек А (1; 2) и В (-3; 4). 16 На оси ординат найти точку, равноудаленную от точек А (-3; 5) и В (6; 4). 17 Определить рдиус окружности, которая проходит через точку А (-24 1) и имеет центр в точке С (2; -3). 18 Дан четырехугольник ABCD: А (-1; 7), В (5; 5), С (7; -5), D (3; -7). Доказать, что четырехугольник, вершинами которого служат середины сторон данного четырехугольника, есть параллелограмм. 19 Дана точка М (2; -1; 1). Найти координаты точек, симметричных с точкой М: а) относительно начала координат; б) относительно координатных плоскостей в) относительно координатных осей. 20 Даны тройки точек: а) б) в) Указать среди них тройки точек, лежащих на одной прямой. 21 Доказать, что треугольник АВС: А (3; 5; - 4), В (-1; 1;2), С (-5; -5;-2) является равнобедренным. 22 Доказать, что четырехугольник, вершины которого находятся в точках А (7; 2; 4), В (4; -4;2), С (6; -7;8), D (9; -1; 10) является квадратом. 23 Даны вершины треугольника А (2; -1; 4), В (3; 2; -6), С (-5; 0;2). Вычислить длину медианы АМ. 24 Найти радиус сферы, проходящей через точку А (-2; 0; 2) и имеющей центр в точке С (1; 1; 6). 25 На прямой, проходящей через точки А (1; 0; 4) и В (3; -1; 2), найти точку С такую, чтобы АС = 3 АВ и точка В лежала между точками А и С. 26 Найти отношение, в котором каждая из координатных плоскостей делит отрезок АВ: А (2; -1; 7) и В (4; 5; -2). Найти координаты делящей точки. 27 На оси О х найти точку, равноудаленную от точек А (1; 2; 3) и В (-2; 1; 3) 28 В треугольнике с вершинами А (5; 0; 0), В (1; 1; 1), С (3; -1;2) найти внутренние углы.
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 691; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.231.128 (0.008 с.) |

 и точки
и точки  . Определить координаты конца вектора
. Определить координаты конца вектора  (3; 4),
(3; 4),  (- 2; 3); б)
(- 2; 3); б)  (-3; 0),
(-3; 0),  (0; 0).
(0; 0). .
. имеет координаты
имеет координаты 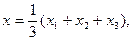
 Найти координаты точки пересечения медиан, если его вершины имеют координаты:
Найти координаты точки пересечения медиан, если его вершины имеют координаты: ;
;