
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действия над векторами в координатной формеСодержание книги
Поиск на нашем сайте
Пусть в декартовой системе координат Охуz даны векторы
т.е. Замечание: в дальнейшем будем считать все координаты точек и векторов декартовыми, если отдельно не оговорено противное. С такими векторами можно выполнить следующие действия: сравнение, сумма (разность), умножение на число, скалярное произведение, найти модуль вектора, угол между векторами и проверить векторы на коллинеарность. Рассмотрим их подробнее: Сравнение Два вектора равны тогда и только тогда, когда равны все их одноименные координаты, Нарушение хотя бы одного равенства говорит о неравенстве векторов, Векторы различных размерностей несравнимы. Операции “ < “ и “ > ” на векторах не заданы; 7.2 Сумма и разность векторов: координаты суммы (разности) двух векторов равны сумме (разности) одноименных координат этих векторов,
(x1; y1; z1) ± (x2; y2; z2) = (x1±x2; y1±y2; z1±z2); 7.3 При умножении вектора на число на это число умножаются все его координаты, l× l×(x1; y1; z1)= (l×x1; l×y1; l×z1); 7.4 Скалярное произведение двух векторов в координатной форме: (8) т. е. скалярное произведение двух векторов равно сумме попарных произведений одноименных координат. Выведем эту формулу:
= х1x2× + y1x2× + z1x2× Векторы т.е. для них поэтому Модуль вектора При получим (9) | т.е. модуль вектора, заданного своими координатами, равен квадратному корню из суммы квадратов его координат; 7.6 Косинус угла между векторами (при (10) cos( Если перпендикулярности ненулевых векторов, заданных координатами; Условие коллинеарности Пусть векторы х1=lx2, y1=ly2, z1=lz2. Получили, что если выполнено то векторы
Координаты вектора (без разделителей “; “) могут считаться строкой (или столбцом) числовой матрицы. При коллинеарности нескольких векторов матрица А, для которой такие векторы являются строками (или столбцами), имеет ранг r(A)=1 (наибольшее количество линейно независимых строк или столбцов). Все миноры для А порядков выше 1 являются нулевыми. Для двух векторов пространства Охуz:
– условие коллинеарности двух трехмерных векторов, заданных координатами. Для трех и более векторов либо при большей размерности аналогично составляются все возможные миноры второго порядка для матрицы А и приравниваются к нулю; 7.8 Координаты вектора Если известны координаты начальной точки (11)
|
||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 1836; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

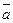 =x1×
=x1× 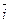 +y1×
+y1× 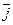 +z1×
+z1×  и
и 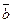 =x2×
=x2× 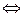 (х1 = х2, y1=y2, z1=z 2 ).
(х1 = х2, y1=y2, z1=z 2 ).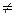
 +
+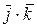 +
+ + z1y2×
+ z1y2× 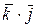 + z1z2×
+ z1z2×  ×
×  ×
× 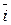 =
=  , |
, | 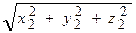 ,
,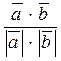 =
=  .
.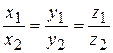 ,
,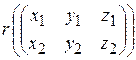 =1 следовательно
=1 следовательно 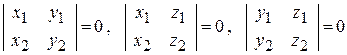 .
.
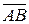
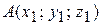 и конечной точки
и конечной точки  вектора
вектора  и
и  (из координат конечной точки вычитаются соответствующие координаты начальной точки),
(из координат конечной точки вычитаются соответствующие координаты начальной точки),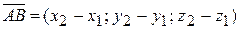 ;
;


