
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деление отрезка в данном отношенииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть на плоскости Оxy заданы две различные точки M1(x1; y1) и М2(x2; y2). Проведем через эти точки прямую L, пусть М (х; у) - некоторая точка прямой L, не совпадающая с М2 (рис.15).
Точка М делит отрезок М1М2 в отношении l, если (13)
Очевидно, что: 1) l>0 лишь в случае, когда точка М лежит между точками М1 и М2; 2) l=0, если точки М и М1 совпадают; 3) l< 0 в случае, если точка М лежит вне отрезка М1М2; 4) Если М отлична от М1, то
Наша задача заключается в том, чтобы найти координаты (x; y) точки М, делящей отрезок М1М2 в заданном отношении l¹-1, если известны координаты (х1, у1) и (x2; y2) точек М1 и М2. Перепишем равенство (13) в координатной форме: (х-х1; у-у1)=l(х2-х; y2-у), т.е. Решая первое уравнение относительно х, второе уравнение относительно у, получим (14) x= Формулы (14) называются формулами деления отрезка в данном отношении. В частности, если l=1, т. е. если Следовательно, каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Для нахождения координат точки М(х; у; z), делящей отрезок прямой пространства, определенного точками M1(x1; y1; z1) и M2(x2; y2; z2), в заданном отношении l, аналогичными рассуждениями получаем формулы (15) x=
В частности, если точка М (х; у; z) делит отрезок М1М2 пополам, то l=1 и формулы (15) примут вид x=
7.11 Перечисленные операции обобщаются и для векторов с любым конечным числом переменных n: пусть даны векторы тогда для них
Если
Для точек вектор расстояние |АB|= середина
Все свойства перечисленных действий, рассмотренные ранее (не в координатной форме), сохраняются. Пример 5 Даны векторы Для них 1) Перечислить равные векторы; 2) Найти 2× 3) Вычислить скалярное произведение векторов 4) Вычислить 5) Найти модули векторов 6) Найти угол между Решение: 1) Среди перечисленных векторов только одна пара совпадающих векторов:
2) 2× =(2 –3 + 1; 4 – (-6) +2; 6 – 0 +3)= (0; 12; 9), 2× 3)
4) 1 способ:
2 ( 2 способ: ( = 2×
( ( 5) Модули векторов:
6) Косинус угла между векторами cos ( ( Пример 6 Даны точки пространства А(1; 2; 3) и В(4; -2; 1). Найти координаты точек М1 – делящей отрезок АВ в отношении и М2 – середины отрезка АВ. Решение: Для нахождения координат точки М1 воспользуемся формулами (15) x= x= Получили точку М1(1,857; 0,857; 2,429).
Если точка М2 делит отрезок АВ пополам, то ее координаты найдутся как полусумма координат концов отрезка: x= Получили точку М2(2,5; 0; 2). Ответ: М1(1,857; 0,857; 2,429), М2 (2,5; 0; 2). Векторное произведение
|
||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 727; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.121.160 (0.009 с.) |

 =l×
=l×  .
.
 .
. , y=
, y=  – координаты искомой точки М.
– координаты искомой точки М. , точка М(х; у) является серединой отрезка М1М2. Формулы (14) примут вид x =
, точка М(х; у) является серединой отрезка М1М2. Формулы (14) примут вид x =  , y =
, y =  .
. , y=
, y=  , z=
, z=  .
.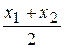 , y=
, y=  , z=
, z=  .
. ,
, 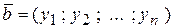 ,
, ,
, ,
, ,
, ,
,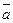 ¹0,
¹0, 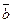 ¹0 и
¹0 и  , то
, то  ^
^  ,
, ,
,  ,
, ,
,  векторы
векторы  и
и 
 ,
,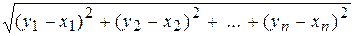 ,
, .
. =(1; 2),
=(1; 2),  =(1; 2; 3),
=(1; 2; 3),  =(3; 2; 1).
=(3; 2; 1). ;
;
 =
=  ,
, 67 0 , в радианах (
67 0 , в радианах (
 =0,4
=0,4 , которые при
, которые при  , y=
, y=  , z=
, z=  .
. , y=
, y=  , z=
, z=  .
.


