Дихотомическое деление отрезка

 

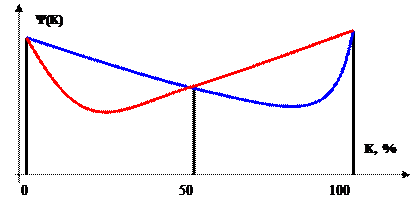
Деление отрезков пополам аналогично методу «поразрядного уравновешивания», который используется в аналого-цифровых преобразователях. В этом случае после испытания со значением 100 следует осуществить испытание со значением 50. Но если новая целевая функция будет меньше предыдущей, то не понятно, где находится оптимальное значение – больше или меньше, чем 50 (см. рис. 6, два варианта функции при фиксированных трех ее значениях). Поэтому для принятия решения требуется осуществить испытания еще и при других значениях. Например, при значениях, соответствующих серединам полученных интервалов, то есть при 25 и при 75. Только имея четыре точки, мы могли бы отбросить ту точку, которая соответствует наибольшему значению целевой функции при условии, что она не является внутренней точкой.

Поэтому рассмотренный метод дихотомического деления (деления на два) не является оптимальным.

Рис. 6. Невозможность определения по трем точкам функции Ψ(K) положения отрезка, содержащего минимум

 

Метод чисел Фибоначчи

 

В современной интерпретации метод был предложен Кифером, но его корни восходят к математику XIII века Фибоначчи и даже к более ранним исследованиям Евклида [10].

На последнем шаге самый эффективный шаг для отыскания точки, наиболее близкой к минимуму – это деление отрезка пополам и определение значения целевой функции в этой точке (при условии, что мы не принимаем в расчет производные целевой функции). Обозначим длину отрезка от начала последнего интервала до точки исследования L _N. Индекс N относится к номеру эксперимента. Тот факт, что на последнем шаге интервал делится пополам, означает, что отрезок на предпоследнем шаге составил двойное значение этого шага: L _N-1 = 2 L _N.

На шаге N –2 отрезок должен быть равен сумме отрезков на предпоследнем и на последних шагах: L _N-2 = L _N-1 + L _N.

Методом математической индукции можно доказать, что аналогичное равенство имеет место на каждом шаге: L _K-1 = L _K + L _K+1. Этому свойству соответствует ряд чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…

Последовательность чисел Фибоначчи формируется следующим путем: R ₀ = 1, R ₁ = 1, R _i+2 = R _i + R _i+1. Таким образом, коэффициент деления отрезка на шаге с номером i равен a_i = R _i-2/ R _i. То есть на последнем шаге a _N = 1/2, на предпоследнем a _N-1 = 1/3, и далее в этом направлении: 2/5, 3/8, 5/13, 8/21, 13/34, 21/55, 34/89, 55/144 …

 

Метод золотого сечения

 

Метод золотого сечения исключает зависимость от количества опытов. Согласно этому методу требуется a = a _N = a _N-1 (при N →∞). Поэтому значение a можно найти как отношение соответствующих чисел Фибоначчи при N →∞. Можно к этому числу подойти иным путем.

Рассмотрим отрезок AB на рис. 7. Нам необходимо выбрать две произвольные точки C и D внутри этого отрезка. После этого мы будем знать значения целевой функции в четырех точках: A, B, C и D. По результатам анализа этих функций мы отбросим одну из крайних точек отрезка. По результату у нас останется уменьшенный отрезок, либо AD, либо CB.

С оставшимся отрезком нам требуется продолжать такие же эксперименты. То есть получившийся отрезок также надо исследовать, и потребуется две внутренних точки. Но одна внутренняя точка в каждом из этих отрезков уже имеется. Поэтому мы хотим выбрать соотношение деления так, чтобы эта внутренняя точка входила в этот требуемый набор.

Пусть AC / AB = DB / AB = a. Мы хотим, чтобы было справедливым также соотношение CD / AD = a, то есть: a / 1 = (1 – 2 a) / (1 – a).

Отсюда: a – a ² = 1 – 2 a, или a ² – 3 a + 1 = 0.

.

Поскольку по определению a < 1, следует выбрать знак «минус».

Получаем a = 0,381966…≈ 0,382.

 

Рис. 7. Метод золотого сечения

 

Покажем, что при N →∞ метод Фибоначчи эквивалентен методу золотого сечения. Действительно, приведенная выше последовательность в десятичных дробях имеет вид: 0,4; 0,375; 0,3846; 0,3809; 0,38235, 0,381818; 0,3820; 0,381944. Эта последовательность приближается к коэффициенту золотого сечения.

Иногда для обозначения золотого сечения применяется обратная величина b =1/ a ≈ 2,6178.

Также для обозначения золотого сечения используется коэффициент

τ = b – 1 = 1,6178.

Эти величины взаимосвязаны. В греческой архитектуре наиболее красивым считался прямоугольник, стороны которого соотносились как 1: 1,618, то есть 1: τ – «золотой» прямоугольник. Если в таком прямоугольнике выделить квадрат, то оставшийся прямоугольник также будет «золотым». Коэффициент b показывает сумму двух сторон прямоугольника в единицах длины меньшей стороны, коэффициент a – отношение меньшей стороны к этой сумме. При делении отрезка AB мы выбираем точку C таким образом, чтобы получившиеся отрезки относились своими длинами как стороны «золотого» прямоугольника.

Не следует путать «золотой» прямоугольник с прямоугольником, стороны которого соотносятся как 1: 1,41 (корень из двух). Такое соотношение используется для типовых размеров бумаги и дает то преимущество, что при делении листа пополам получается прямоугольник с таким же соотношением сторон.