
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтетические критерии оптимальностиСодержание книги
Поиск на нашем сайте
Если имеется несколько величин, которые необходимо минимизировать или максимизировать, то стоимостный функционал целесообразно задавать в такой форме, чтобы он учитывал все эти величины. В теории рекомендуется вносить весовые коэффициенты. Но лишь при поверхностном взгляде кажется, что это легко решает проблему. При сопоставлении нескольких величин количество коэффициентов требуется на один меньше, чем величин (поскольку общий масштабный множитель не влияет на результат, так что один из коэффициентов можно произвольно положить единичным). Но для сложения разнородных величин необходимо их все привести к общим единицам, лучше – безразмерным. Естественный множитель может быть взят, если известна величина того или иного минимума для процесса, который может быть взят за некий эталон. Естественными множителями могут быть взяты величины, обратно пропорциональные этим значениям. Другой способ объединения критериев – отыскание их общей природы и формирование критерия промежуточной природы. Например, пусть имеются два критерия:
Пусть для некоторой вполне приемлемой траектории на заданном интервале эти критерии принимают значения Тогда сокращаем эти величины на общий множитель 100 и от полученных величин берем обратные значения, которые и используем в качестве весовых коэффициентов:
По второму способу мы усматриваем, что в подынтегральном выражении используются различные степени модуля величины e, следовательно, для формирования синтетического критерия можно попробовать взять среднее геометрическое от этой степенной функции, а именно:
Пример. Пусть имеется задача оптимизировать как время, так и стоимость проезда. Естественно, что эти затраты могут экономиться лишь ценой друг друга, т.е. можно экономить время, расходуя больше денег, и экономить деньги, теряя больше времени. Задача отыскания приемлемого компромисса, по сути, сводится к задаче сведения цены ресурсов в единой шкале цен – либо следует оценить время в рублях, либо рубли в часах, что, вообще говоря, одно и то же. Скажем, если заработок путешественника составляет 100 руб. в час, можно допустить, что экономия часа вполне стоит того, чтобы оплатить ее хотя бы половинной ценой часового заработка. Это дает следующий естественный критерий:
где Экспертный способ определения цены: если трудно назвать цену определенной работы, то зато, как правило, оказывается достаточным просто назвать две предельные цены, а именно: заведомо заниженную и заведомо завышенную. Скажем, «сколько стоит сходить вынести мусор?». Допустим, вы легко отдали бы 5 руб. человеку, который сделает это за вас, но вы не дали бы за эту работу 20 руб. Следовательно, истинная цена для вас лежит где-то посредине. «Серединой» можно называть среднее арифметическое и среднее геометрическое с равной степени обоснованности, если нет особых оснований для предпочтения того или иного способа усреднения (среднее геометрическое, это среднее по логарифму). В данном примере среднее арифметическое дает 12,5 руб., а среднее геометрическое – 10 руб. Разница в результатах пренебрежимо мала, но если требуется еще большая обоснованность решения, то можно указать середину между этими «серединами», т.е. 11 руб. Нормативные оценки. Допустим, в электронике было принято, что стоимость затрат складывается из трех приблизительно равных величин: заработная плата разработчиков, стоимость комплектации и сопроводительные работы по изготовлению (монтажные, слесарные, сборка, покраска, маркировка, и т.п.). Это позволяет при обоснованной оценке одной из этих компонент прогнозировать стоимость других. Недостаток состоит в том, что вследствие развития технологий и в силу особенностей изделия эти пропорции могут сильно не выдерживаться. Однако есть много случаев, когда даже не вполне точная оценка необходима, и это лучше, чем отсутствие оценки. Оптимизация ансамбля систем
При моделировании может быть создано несколько параллельно работающих систем. Возможны два случая: а) параллельное моделирование систем с одинаковыми объектами и различными регуляторами; б) параллельное моделирование разных объектов с одинаковыми регуляторами. В случае (а) это может ускорить процесс отыскания экстремума и сделать его более наглядным. Например, если мы не знаем, следует ли увеличить или уменьшить данный параметр регулятора, мы можем попробовать сделать и то и другое последовательно, а можем реализовать и то и другое параллельно. В случае поиска оптимальной настройки с реальным объектом зачастую приходится осуществлять пробную девиацию настраиваемого параметра. Такая девиация позволяет определить направление дальнейшего изменения этого параметра. При моделировании мы не ограничены одним объектом, можем моделировать параллельно два или даже больше объектов. Это избавляет от необходимости пробной девиации. Случай (б) позволяет осуществлять расчет робастных регуляторов, то есть таких регуляторов, которые обеспечивают удовлетворительное решение задачи не только для фиксированных параметров объекта, но при их изменении в некотором небольшом (заранее известном) диапазоне. Действительно, если нужен регулятор, успешно работающий с объектом при условиях изменения его параметров в некотором диапазоне, мы можем параллельно моделировать несколько систем с одинаковыми регуляторами, но разными объектами. При этом разные настройки параметров объектов соответствуют крайним и (или) наиболее нежелательным сочетаниям параметров объекта. Регулятор, который даст одновременно наилучшие результаты для всех объектов из этого перечня, будет робастным, в том смысле, что он будет успешным в заранее заданном диапазоне изменений параметров объекта. Критерий качества при этом должен учитывать в равной мере (или, возможно, с весовыми коэффициентами) качество каждой из моделируемых систем.
|
||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |


 ,
,  .
.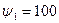 ,
,  .
. .
. .
. ,
, ,
,  и
и  - затраты времени и денег на проезд отдельных участков пути.
- затраты времени и денег на проезд отдельных участков пути.


