Метод покоординатного спуска

 

Метод покоординатного спуска предполагает на первом шаге изменение только одного аргумента (одной координаты поверхности). При этом остальные параметры «замораживаются», то есть не изменяются. По этой первой координате осуществляется одномерный поиск, пока не будет достигнут минимум. Далее эта координата замораживается, и спуск идет по следующей координате. После отыскания минимума по второй координате она также «замораживается», и спуск идет по третьей координате и так далее. После того, как все координаты будут перебраны, требуется возвращение к первой координате и повторение спуска по ней, потом – по второй координате и так далее. Процесс повторяется до тех пор, пока приращение целевой функции не будет столь малым, что дальнейший поиск будет признан нецелесообразным, или после того, как лимит максимально допустимого количества экспериментов будет исчерпан.

Преимущество данного метода состоит в алгоритмической простоте. Независимо от количества аргументов, метод легко алгоритмически описывается и может быть реализован.

К недостаткам данного метода следует отнести возможность зависания на гребне оврага (см. рис. 7), а также зависимость результата от последовательности аргументов.

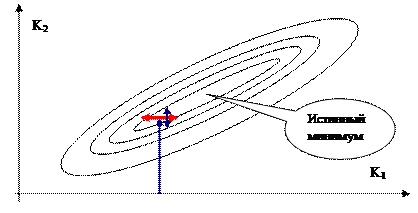
Рис. 7. Зависание на ложбине при методе покоординатного спуска

 

Проблема «зависания» показана на рис. 7. После достижения ложбины «оврага» (также как после попадания на гребень при отыскании максимума) любое движение вдоль осей приводит к увеличению целевой функции, поскольку сопряжено с подъемом из оврага. Однако истинный минимум лежит в направлении вдоль ложбины этого оврага, но движения в этом направлении не будет происходить, или оно будет крайне медленным.

Эта проблема исчезла бы, если бы ложбина оврага лежала по направлению одной из осей. Поскольку функцию повернуть трудно (или невозможно), можно повернуть оси поиска, то есть искать не вдоль осей X и Y,а по направлению ложбины оврага и (на всякий случай) в ортогональном направлении.

 

Метод Розенброка

 

Метод Розенброка состоит в повороте осей поиска по результатам первых шагов метода покоординатного спуска. Новых оси получают поворотом старых осей. Положение новых осей может быть получено линейным преобразованием старых осей. Пусть имеется n аргументов целевой функции. После оптимизации по каждому из n аргументов получаем точку X _n. В этой точке ни один из аргументов не совпадает со стартовым значением этой величины. После очередной процедуры оптимизации получаем точку X _2n. В этой точке ни одна из координат не совпадает с координатой из точки X _n. Вектор X _2n - X _n дает направление нового поиска, а ортогональные этому вектору другие векторы – направления дополнительных поисковых сканирований. Этот метод аналогичен развороту координат в таком направлении, чтобы первая координата по направлению совпала с линией оврага.

 

Метод Хука – Дживса

 

Метод Хука – Дживса является удачной модификацией метода покоординатного спуска. В соответствии с этим методом вначале выполняю серию из n шагов. Затем делают дополнительный шаг в направлении вектора X _k – X _k-n.

 

3.8.9. Метод Нелдера – Мида (деформируемого многогранника)

 

Если искомых параметров n, то следует строить многогранник с n + 1 вершиной. В частности при оптимизации по двум параметрам строится треугольник. Вначале вершины этого многогранника выбираются произвольно. Эти вершины следует ранжировать по величине целевой функции. Вершина с наибольшим значением (худшая) должна быть исключена в новом многограннике. Вычисляется точка центра тяжести многоугольника. В случае треугольника она лежит на точке пересечения медиан. Из худшей вершины через точку центра тяжести проводится луч, после пересечения этим лучом точки ЦТ откладывается отрезок такой же длины, как из худшей вершины до этой точки. Новая вершина заменяет худшую. Если оказывается, что новое значение целевой функции имеет самое лучше значение среди других вершин многогранника, то расстояние в этом направлении увеличивают, что дает новую точку. В новом многограннике опять отыскивается худшая вершина и метод повторяется заново.

 

3.8.10. Метод Флетчера-Рився (сопряженных градиентов)

 

Этот метод основан на понятии сопряженных векторов. Векторы A и B называют Q -сопряженными, если A^TQB = 0, где Q – положительно определенная квадратная матрица того же порядка, что и размер N векторов A и B. Частный случай сопряженности – ортогональность векторов, когда Q – единичная матрица, A и B – вектор-столбцы. Более подробно с методом можно ознакомиться в [1, с.163].

 

Метод Девидона – Флетчера – Пауэлла (переменной метрики)

 

Этот метод можно рассматривать как усовершенствованный метод Ньютона второго порядка [1, с.164]. Требуется отыскать точку, в которой градиент целевой функции равен нулю. Отыскание нуля градиента осуществляется методом Ньютона. Нуль градиента может быть также найден методом секущих.

 

Метод локальной оптимизации

 

Метод локальной оптимизации [1, с.182] предполагает при движении из каждой новой точки давать приращение по каждой координате отдельно, получать набор ближайших значений параметров, анализировать набор значений целевых функционалов, и двигаться в направлении минимального функционала из этого набора. В таком случае порядок начертания параметров регулятора не будет иметь значения, в этом смысле этот метод предпочтителен, поскольку движение идет преимущественно по той координате, по которой градиент целевого функционала существенней.

ПРИМЕР 2. Получили регулятор после 5000 шагов [60/40/5]. После следующей итерации, например, получаем [60,5/40,2/5,1]. Изменения всех коэффициентов идут в одну сторону. Поэтому можно предположительно начать новую итерацию не с новых значений, а с тех, которые отличаются от старых на удвоенную величину полученных приращение, то есть [61/40,4/5,2].

ПРИМЕР 3. В тех же условиях, что и пример 2, после третьей итерации получаем [60,8/40,4/5,2]. Это говорит о том, что изменения коэффициентов идут монотонно, и в одном направлении, то есть мы достаточно далеки от экстремума. Скорее всего, следует повысить точность в настройках оптимизации, поскольку оптимизация, предположительно, завершается по признаку достаточно малого отличия полученного результата от истинного экстремума, то есть определена слишком грубая точность результата.

Этот метод может привести к «застреванию» в точке локального экстремума. Повысить эффективность метода можно применением метода запретов, в соответствии с которым запрещено посещать ранее посещенные точки. В результате возникает тенденция к выходу из локальных экстремумов.

Другой способ выхода из локальных экстремумов – по окончании процедуры оптимизации повторить ее с новыми стартовыми значениями.

Для случая оптимизации ПИД-регуляторов, как минимум, можно попытаться увеличить все коэффициенты в 1,2 – 1,5 раза и уменьшить во столько же раз. Если каждый раз результат оптимизации будет тем же, можно надеяться, что результат является глобальным оптимумом. Для других задач изменения стартовых условий могут потребоваться существенно больше.

 

Эволюционные методы