
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автоматизированное проектирование систем управленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Факультет АВТФ В. А. Жмудь Автоматизированное проектирование систем управления Учебное пособие
Новосибирск
З-86.53-05 УДК 621.375.087.9 Ж 774
Жмудь В.А. Автоматизированное проектирование средств и систем управления (АПССУ): Учеб. пособие / Новосибирск. Изд-во НГТУ, 2012. 100 с.
Рецензент д-р техн. наук, проф. Г. А. Французова
Пособие предназначено для студентов очного и заочного отделения, обучающихся по направлению подготовки 220200.62 «Автоматизация и управление», по дисциплине «Автоматизированное проектирование систем управления», (магистр, 1 курс). Пособие содержит учебные материалы и методические рекомендации по самоконтролю (вопросы для самопроверки). Работа выполнена по заданию Министерства образования и науки РФ, проекты № 7.559.2011 (Темплан). Для успешного овладения курсом требуется успешное обучение по ранее изученным математическим дисциплинам.
© Новосибирский государственный технический университет, 2012
ВВЕДЕНИЕ Вопросы для самоконтроля
1. В каком порядке выполняются следующие этапы по проектированию технических проектов: ОКР, Изготовление опытных образцов, НИР, Испытания и приемка, Разработка технической документации. 2. В чем суть проектирования методами «сверху вниз» и «снизу вверх»? 3. Кем разрабатывается ТЗ на ОКР и почему? 4. Кем разрабатывается ТЗ на НИР и почему? 5. Какой этап предшествует техническому проектированию? 6. Назовите основные этапы ОКР. 7. Перечислите основные цели автоматизации проектирования. 8. Назовите основные методы уменьшения трудоемкости инженерного труда. 9. Какими методами достигается улучшение качества проектирования? 10. Какие из перечисленных методов используются для сокращения трудоемкости проектных работ: автоматизация оформления проектной документации, совмещенное (параллельное) проектирование, вариативное проектирование и оптимизация? 11. Какие из перечисленных задач автоматизации проектных работ могут противоречить друг другу: сокращение трудоемкости проектирования, сокращение себестоимости проектирования, сокращение цикла «проектирование – изготовление»? 12. Назовите основные виды обеспечения САПР. 13. Классический и системный подходы. Два определение системного подхода, их отличия. 14. Какие преимущества дает использование электронных чертежей (схем) перед бумажной технологией? 15. Для чего нужна ассоциативная связь между принципиальной электрической схемой и редактором печатных плат? 16. Какие основные программные пакеты входят в EDA-систему? Проектирование элементов мехатронных систем Мехатроника – инструментарий для разработки робототехники
Мехатроникой называют «систему средств совместного проектирования и моделирования узлов точной механики с электронными, электротехническими и компьютерными компонентами, обеспечивающими проектирование и производство качественно новых модулей, машин и систем с интеллектуальным управлением их функциональными движениями», «технологии трансляторов между EDA- и MCAD- системами» [2]. Иными словами, это – инструментарий для разработки интеллектуальных подвижных систем, как правило, робототехнических компонент (манипуляторов, беспилотных транспортных средств и иных интеллектуальных электромеханических устройств и систем). Первые электромеханические системы состояли, как правило, из условно независимых компонент: механических узлов, электрических узлов и электронных управляющих систем. Деление системы на подсистемы осуществляется для более простого описания ее функционирования, путем выделения отдельных функций и соотнесения их по признаку, какие функции какой подсистемой выполняются. Например, систему управления радиолокатором можно разделить на чисто механическую часть, состоящую из антенны, редукторов и элементов конструкции, электромеханическую – электродвигатель, электротехническую – усилитель для питания электродвигателя, датчики положения и управляющую электронику. Современные электромеханические системы уже не могут быть адекватно разделены на условно независимые компоненты: механические узлы, электрические узлы и цифровые электронные управляющие системы. Если такое деление искусственно осуществить, оно не вполне точно будет отражать реальную систему. Промышленность выпускает готовые системы, содержащие встроенные датчики угла поворота, прецизионные системы управления углом поворота, двигатели и редукторы – все в единой сборке. Для управления такой системой достаточно подать на нее электропитание и цифровые сигналы предписанных углов поворота (в соответствии с протоколом обмена). Встроенная управляющая система может содержать собственный микроконтроллер и общаться с внешним устройством как обычный или промышленный компьютер, или, как, например, периферийное устройство (сканер, принтер и т.п.). Вопросы для самоконтроля
1. Что такое мехатроника? 2. Что называют проектом при программировании структуры цифроаналогового устройства на основе аналогового процессора или микроконтроллера? 3. Для каких целей могут быть использованы программные средства MexBIOS Development Studio и VisSim? Какие из указанных программных средств (или оба) позволяют автоматически осуществлять оптимизацию регуляторов для замкнутых систем? 4. Перечислите достоинства программы VisSim.
Требования к физической реализуемости модели
Все элементы системы должны быть физически реализуемы. Это условие формально требует, чтобы степень числителя была меньше степени знаменателя. Действительно, следует учесть, что аргумент s представляет собой некий аналог частоты. С ростом частоты передаточная функция отдельных элементов не обязательно ниспадает, но если продлить этот рост частот достаточно далеко, то передаточная функция любого реального объекта непременно ниспадет до сколь угодно малых величин. Мало того: для любого объекта всегда можно указать такие частоты, на которых передаточная функция не просто мала, а отклик объекта на этих частотах строго отсутствует (либо намного меньше шумов его измерения). Частотные характеристики, как правило, представляют в логарифмическом масштабе, поэтому на графике достаточно быстро достигается «практическая бесконечность», т. е. очень большие значения частоты и значения передаточной функции, как и «практический нуль», т. е. очень маленькие значения этих величин. На логарифмических графиках наглядно видны значения частот, во много раз превышающих область частот пропускания объекта. Таким образом, правая часть логарифмической амплитудно-частотной характеристики (ЛАЧХ) любого реализуемого звена должна на графике ниспадать вниз, чем правее, тем ниже. Это достигается только при условии, что знаменатель указанной дробной передаточной функции больше, чем числитель. Иногда в отношении отдельных звеньев этим требованием пренебрегают, поскольку полоса пропускания этих звеньев может оказаться существенно шире полосы пропускания объекта. Так, затуханием отдельных элементов можно пренебречь в сравнении с затуханием других звеньев, входящих в тот же контур. Если же какое-либо звено является единственным звеном рассматриваемого контура, то в этом контуре нет других более инерционных звеньев, в сравнении с которыми можно было бы пренебречь затуханием данного элемента. В этом случае указанный элемент недопустимо описывать безынерционным звеном. Даже ограничиваться рассмотрением лишь отличием степени знаменателя от степени числителя также недостаточно для адекватного анализа устойчивости любого реального контура с отрицательной обратной связи. Однако если в контуре присутствует элемент запаздывания и если достоверно известно, что влияние следующей постоянной времени модели на фазо-частотную характеристику (ФЧХ) существенно меньше, допускается ограничивать рассмотрение динамической части объекта элементами первого порядка. 3.3. Формализация требований к системе: целевая функция
Целевая функция может быть сформирована, например, следующим образом:
Это – положительно определенная функция, то есть она не может быть отрицательной ни при каких значениях ее аргументов. Требуется найти такие значения коэффициентов регулятора, при которых целевая функция достигает минимального значения. Поскольку ошибка в системе зависит от коэффициентов регулятора, то и вся целевая функция будет зависеть от этих коэффициентов. Решение этой задачи называется оптимумом, в нашем случае – минимум. Следует различать локальные и глобальный минимумы. Локальные минимумы – это такие решения, при которых небольшие изменения любого параметра вызывают рост целевой функции, однако, это не относится к любым изменениям этих параметров. Глобальный минимум может быть лишь один – это такое решение, которое обеспечивает наименьшее значение целевой функции для всех параметров из области их допустимых значений. Могут быть применены различные алгоритмы поиска минимума. Правильность выбора метода оптимизации зависит от свойств задачи: наилучший метод для одной задачи может оказаться наихудшим или вовсе неприменимым для другой задачи. Можно разбить методы оптимизации на следующие виды: 1. Итеративный поиск. 2. Случайный перебор. 3. Систематический перебор. 4. Генетические алгоритмы. Итеративный поиск эффективен в том случае, если целевая функция плавно изменяется при плавном изменении ее аргументов. Гладкость предполагает, что небольшое приращение любого аргумента дает небольшое приращение функции. В этом случае можно предполагать, что в точках максимума или минимума целевой функции приращение любого аргумента в любом направлении дает приращение целевой функции только в одном направлении, а именно: в случае максимума целевая функция уменьшается при любом приращении аргумента, а в случае минимума – увеличивается. Во всех остальных точках малое положительное приращение какого-либо из аргументов дает малое приращение величины целевой функции одного знака, а малое отрицательное приращение этого же аргумента даст малое приращение противоположного знака. Поэтому итеративные процедуры осуществляют изменения всех аргументов (поочередно или совместно) до тех пор, пока не будет достигнута такая ситуация, при которой любое приращение любого из аргументов вызовет лишь увеличение целевой функции. Это будет означать достижение, по меньшей мене, локального минимума. Проверка на глобальность этого минимума, то есть на наличие других минимумов, необходима, поскольку могут существовать несколько минимумов. Для того чтобы можно было применять итеративный поиск, требуется обеспечить специальные свойства целевой функции. В частности, она должна быть гладкой. Если это не так, то итеративный метод не даст результата, поскольку в этом случае результат приращения целевой функции при каком-либо малом приращении аргумента никаким образом не связан с результатом приращения этой целевой функции ни при каком ином сколь угодно малом приращении этого же аргумента. Для такой ситуации может быть применен лишь случайный или систематический перебор. Систематический перебор предполагает решение задачи для всех возможных сочетаний всех параметров объекта. Эта процедура чрезвычайно громоздка для любой практической задачи, поэтому затруднительно указать случаи целесообразности ее применения. Случайный перебор отличается от систематического лишь тем, что выбор параметров регулятора осуществляется не по какому-либо наперед заданному закону и не с целью перебора всех возможных вариантов, а случайным или псевдослучайным образом. Этот метод позволяет сократить процедуру настройки регулятора в предположении, что в достаточной степени удовлетворительный (хотя и далеко не оптимальный) результат может выпасть значительно раньше, чем будут исследованы все возможные сочетания всех параметров. Это позволит прекратить дальнейший поиск, выбрав это решение. Этот метод напоминает попытку угадать счастливое число в казино, поэтому он получил название метода Монте-Карло (по названию столицы игорного бизнеса). Именно такой метод применяется при «оптимизации» регуляторов в программе Simulink. Хотя результат такого численного поиска зачастую вполне удовлетворительный, строго говоря, этот результат не является результатом оптимизации, поскольку невозможно исключить, что могут быть найдены лучшие решения, дающие меньшее значение целевой функции. Все же следует признать, что этот метод – единственный приемлемый метод для случая отсутствия какой-либо гладкой зависимости между изменениями аргументов и изменениями самой функции. Применительно к задаче численной оптимизации регулятора ситуация далеко не столь бесперспективна: целевая функция, как правило, всегда является гладкой, и производная этой целевой функции по любому параметру может указать на то направление изменения этого параметра, которое ведет к минимуму целевой функции. Действительно, если производная положительна, то положительное приращение параметра увеличивает функцию. Следовательно, необходимо уменьшать этот параметр. Если производная отрицательна, следует этот параметр увеличивать, а если она равна нулю, данная точка находится на минимуме при фиксированных значениях остальных параметров, и, следовательно, как минимум, эта точка находится в «ложбине», которая ведет к минимуму. Дальнейшее изменение этого параметра целесообразно делать лишь совместно с изменениями других параметров. Если частные производные целевой функции по всем параметрам равны нулю, данная точка может оказаться минимумом. Специальные случаи, когда это не так, могут быть учтены процедурой поиска, в итоге которого должна быть найдена точка, в которой любые линейные комбинации любых малых приращений любых параметров порождают лишь увеличение целевой функции. Оптимизация ансамбля систем
При моделировании может быть создано несколько параллельно работающих систем. Возможны два случая: а) параллельное моделирование систем с одинаковыми объектами и различными регуляторами; б) параллельное моделирование разных объектов с одинаковыми регуляторами. В случае (а) это может ускорить процесс отыскания экстремума и сделать его более наглядным. Например, если мы не знаем, следует ли увеличить или уменьшить данный параметр регулятора, мы можем попробовать сделать и то и другое последовательно, а можем реализовать и то и другое параллельно. В случае поиска оптимальной настройки с реальным объектом зачастую приходится осуществлять пробную девиацию настраиваемого параметра. Такая девиация позволяет определить направление дальнейшего изменения этого параметра. При моделировании мы не ограничены одним объектом, можем моделировать параллельно два или даже больше объектов. Это избавляет от необходимости пробной девиации. Случай (б) позволяет осуществлять расчет робастных регуляторов, то есть таких регуляторов, которые обеспечивают удовлетворительное решение задачи не только для фиксированных параметров объекта, но при их изменении в некотором небольшом (заранее известном) диапазоне. Действительно, если нужен регулятор, успешно работающий с объектом при условиях изменения его параметров в некотором диапазоне, мы можем параллельно моделировать несколько систем с одинаковыми регуляторами, но разными объектами. При этом разные настройки параметров объектов соответствуют крайним и (или) наиболее нежелательным сочетаниям параметров объекта. Регулятор, который даст одновременно наилучшие результаты для всех объектов из этого перечня, будет робастным, в том смысле, что он будет успешным в заранее заданном диапазоне изменений параметров объекта. Критерий качества при этом должен учитывать в равной мере (или, возможно, с весовыми коэффициентами) качество каждой из моделируемых систем.
Итеративный поиск Итеративный поиск предполагает плавное движение от исходной точки по направлению уменьшения результата. Как правило, величина очередного шага определяется историей процесса, а первый и иногда второй и третий шаги делаются практически произвольно. Если увеличение параметра дает уменьшение целевой функции, то далее осуществляется поиск «вовне», то есть осуществляется дальнейшее его увеличение. Может быть использован метод увеличения на фиксированную величину или увеличения в фиксированное количество раз (то есть на фиксированную величину в логарифмическом масштабе). В случае оптимизации регулятора выбор одного из этих двух методов не слишком существенен, поскольку при увеличении, например, коэффициента пропорционального регулятора нарушение устойчивости на практике может быть достигнуто достаточно легко – в несколько шагов. Разумеется, если изначально взят слишком маленький коэффициент, и увеличение осуществляется на небольшой процент, то эта процедура может неоправданно затянуться. Поэтому если увеличение параметра приводит к положительным результатам на одном-двух шагах, это может быть основанием увеличивать (например, удваивать) величину последующего увеличения. Это позволяет достаточно быстро достичь такого коэффициента, который будет идентифицирован как излишне большой. После этого поиск будет осуществляться лишь «вовнутрь», то есть интерполяцией. Если необходимо подобрать один коэффициент с погрешностью 5%, и если имеется граничное значение, то достаточно перебрать 20 значений коэффициентов. Может оказаться, что перебор даст достаточно приемлемый результат по самому простому алгоритму. Например, обычный спуск даст следующую последовательность испытаний (в процентах по отношению к стартовому значению): 100, 95, 90, 85, 80 … и так далее. Такой поиск нельзя назвать оптимальным. Преимущество такого поиска состоит в возможности заранее достаточно просто определить количество требуемых экспериментов. Итеративный поиск можно назвать «осторожным», поскольку при его реализации делаются наименьшие изменения искомой величины от шага к шагу. Этот метод можно применять в начале поиска и в его конце. В начале поиска он позволяет без излишне сложных алгоритмов достичь значений коэффициентов регулятора, которые явно превышают искомые, поскольку приводят систему к потере устойчивости. Если такие эксперименты (с потерей системой устойчивости) разрешены, можно с каждым шагом увеличивать коэффициенты кратно. Это позволяет быстро отыскать верхние границы искомых коэффициентов. Если же такие эксперименты не разрешены, искомые параметры следует увеличивать путем равных приращений. Медленный рост этих коэффициентов обеспечит медленное движение к коэффициентам, при которых устойчивость теряется.
Метод Монте-Карло
Этот метод относится к случайным методам поиска. Значения коэффициентов выбираются случайным путем, подобно действию рулетки во всемирно известном игорном центре. Значения всех коэффициентов задаются случайно, результат в виде целевой функции или в виде таблицы соответствия всем требованиям заносится в память. Лучший результат по окончании эксперимента является глобальным результатом поиска. Недостатком этого метода является необходимость неоправданно большого количества экспериментов. Достоинством метода является более высокая вероятность отыскания глобального минимума вне зависимости от наличия локальных минимумов. Этот метод не требует унимодальной целевой функции на отрезке. Метод Монте-Карло применяется в программе MATLAB (Simulink). Для его применения следует задать желаемые параметры переходного процесса. Решение задачи этим методом не всегда гарантируется или не всегда оптимально. Причина этого состоит в том, что перед началом оптимизации оператор не может заранее знать, какие показатели достижимы, а какие – не достижимы. Например, может быть потребована излишне малая или излишне большая длительность переходного процесса. В первом случае поставленная задача может оказаться нереализуемой, во втором случае – упрощенной по сравнению с потенциальными возможностями регулятора. Если задача ставится не в терминах границ переходного процесса, а в терминах минимума целевой функции, то заранее определять длительность переходного процесса не требуется, он автоматически будет определен по результатам оптимизации.
Метод чисел Фибоначчи
В современной интерпретации метод был предложен Кифером, но его корни восходят к математику XIII века Фибоначчи и даже к более ранним исследованиям Евклида [10]. На последнем шаге самый эффективный шаг для отыскания точки, наиболее близкой к минимуму – это деление отрезка пополам и определение значения целевой функции в этой точке (при условии, что мы не принимаем в расчет производные целевой функции). Обозначим длину отрезка от начала последнего интервала до точки исследования L N. Индекс N относится к номеру эксперимента. Тот факт, что на последнем шаге интервал делится пополам, означает, что отрезок на предпоследнем шаге составил двойное значение этого шага: L N-1 = 2 L N. На шаге N –2 отрезок должен быть равен сумме отрезков на предпоследнем и на последних шагах: L N-2 = L N-1 + L N. Методом математической индукции можно доказать, что аналогичное равенство имеет место на каждом шаге: L K-1 = L K + L K+1. Этому свойству соответствует ряд чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… Последовательность чисел Фибоначчи формируется следующим путем: R 0 = 1, R 1 = 1, R i+2 = R i + R i+1. Таким образом, коэффициент деления отрезка на шаге с номером i равен ai = R i-2/ R i. То есть на последнем шаге a N = 1/2, на предпоследнем a N-1 = 1/3, и далее в этом направлении: 2/5, 3/8, 5/13, 8/21, 13/34, 21/55, 34/89, 55/144 …
Метод золотого сечения
Метод золотого сечения исключает зависимость от количества опытов. Согласно этому методу требуется a = a N = a N-1 (при N →∞). Поэтому значение a можно найти как отношение соответствующих чисел Фибоначчи при N →∞. Можно к этому числу подойти иным путем. Рассмотрим отрезок AB на рис. 7. Нам необходимо выбрать две произвольные точки C и D внутри этого отрезка. После этого мы будем знать значения целевой функции в четырех точках: A, B, C и D. По результатам анализа этих функций мы отбросим одну из крайних точек отрезка. По результату у нас останется уменьшенный отрезок, либо AD, либо CB. С оставшимся отрезком нам требуется продолжать такие же эксперименты. То есть получившийся отрезок также надо исследовать, и потребуется две внутренних точки. Но одна внутренняя точка в каждом из этих отрезков уже имеется. Поэтому мы хотим выбрать соотношение деления так, чтобы эта внутренняя точка входила в этот требуемый набор. Пусть AC / AB = DB / AB = a. Мы хотим, чтобы было справедливым также соотношение CD / AD = a, то есть: a / 1 = (1 – 2 a) / (1 – a). Отсюда: a – a 2 = 1 – 2 a, или a 2 – 3 a + 1 = 0.
Поскольку по определению a < 1, следует выбрать знак «минус». Получаем a = 0,381966…≈ 0,382.
Рис. 7. Метод золотого сечения
Покажем, что при N →∞ метод Фибоначчи эквивалентен методу золотого сечения. Действительно, приведенная выше последовательность в десятичных дробях имеет вид: 0,4; 0,375; 0,3846; 0,3809; 0,38235, 0,381818; 0,3820; 0,381944. Эта последовательность приближается к коэффициенту золотого сечения. Иногда для обозначения золотого сечения применяется обратная величина b =1/ a ≈ 2,6178. Также для обозначения золотого сечения используется коэффициент τ = b – 1 = 1,6178. Эти величины взаимосвязаны. В греческой архитектуре наиболее красивым считался прямоугольник, стороны которого соотносились как 1: 1,618, то есть 1: τ – «золотой» прямоугольник. Если в таком прямоугольнике выделить квадрат, то оставшийся прямоугольник также будет «золотым». Коэффициент b показывает сумму двух сторон прямоугольника в единицах длины меньшей стороны, коэффициент a – отношение меньшей стороны к этой сумме. При делении отрезка AB мы выбираем точку C таким образом, чтобы получившиеся отрезки относились своими длинами как стороны «золотого» прямоугольника. Не следует путать «золотой» прямоугольник с прямоугольником, стороны которого соотносятся как 1: 1,41 (корень из двух). Такое соотношение используется для типовых размеров бумаги и дает то преимущество, что при делении листа пополам получается прямоугольник с таким же соотношением сторон. Случайный поиск
Случайный перебор по методу Монте-Карло алгоритмически наиболее прост, только в отличие от одномерного поиска случайно выбираются все параметры целевой функции. При случайном поиске повторение уже использованных комбинаций нецелесообразно. Поэтому формально предпочтительны не случайные величины, а такие величины, которые отличаются от случайных детерминированным правилом, исключающим повторение эксперимента с набором уже испытанных аргументов. Если при случайном одномерном поиске, например, требуется M = 1000 экспериментов, то при N -мерном поиске потребуется M N экспериментов, число которых растет по степенной зависимости. В случае отыскания коэффициентов ПИД-регулятора при тех же условиях потребуется 109 экспериментов против 103 для одномерного поиска. Случайным поиск может быть применен как частный инструментарий глобального поиска, например, на конечной стадии.
Градиентный метод
Метод градиента предполагает движение по нормали к линиям равного уровня. Основная проблема состоит в определении направления нормали и вычислении длины очередного шага. При движении к минимуму этот метод теоретически дает алгоритм скорейшего спуска. Для вычисления направления и величины очередного шага необходимо знать частные производные целевой функции по каждому аргументу. Частные производные могут быть определены только экспериментально, например, путем пробных экспериментов в точках, отличающихся приращением только по одному из аргументов. Но при этом получается парадоксальная ситуация: для того, чтобы узнать, в какой точке следует сделать следующий эксперимент, требуется предварительно сделать столько экспериментов, сколько аргументов имеется в целевой функции. ПРИМЕР 1. Пусть требуется оптимизировать ПИД-регулятор. На определенном шаге известно значение целевой функции при значениях пропорционального, интегрального и дифференциального коэффициентов регулятора K p=10, K i=5, K d=10. Для краткости можно обозначить эту точку [10 / 5 / 10]. Для вычисления частных производных целевой функции нам требуется сделать испытания, например, с шагом приращения по каждому коэффициенту равным 0,1. Тогда необходимо сделать эксперименты в следующих точках: 1. С приращением по K p [10,2 / 5 / 10]. 2. С приращением по K i [10 / 5,2 / 10]. 3. С приращением по K d [10 / 5 / 10,2]. Таким образом, для вычисления нового шага требуется три новых шага. Кроме того, этот метод работает крайне неудовлетворительно при малом значении градиента, поскольку при этом достоверность результатов эксперимента резко падает в связи с падением отношения сигнал / шум. Действительно, шум измерений (или неопределенность результата эксперимента) всегда имеется, и если градиент падает до нуля, то в итоге измерений получается преимущественно шум. Поэтому градиентные методы при приближении к экстремуму приводят к неоправданному возрастанию количества шагов около точки истинного экстремума, причем, очередные шаги зачастую направлены в сторону, противоположную экстремуму, или превышают требуемую длину шага в разы. Все же первый недостаток является определяющим – на этом основании градиентный метод нецелесообразно применять при оптимизации регулятора. Следует исходить из того, что каждый лишний эксперимент нежелателен, требуется отыскание экстремума за наименьшее число шагов. Метод Ньютона
Метод Ньютона применяется для отыскания нулей сложной функции. Геометрическая интерпретация этого метода состоит в том, что если к функции провести касательную, то она пересечет ось нулевого уровня в точке, более близкой к нулю функции, чем данная исходная точка. Поэтому после ряда таких шагов мы достигнем точки нулевого значения исследуемой функции. Для вычисления направления и величины движения также необходимо знать значения частных производных этой функции по аргументам. Поэтому данный метод также не применим к задаче оптимизации регулятора.
Метод секущих
В отличие от метода Ньютона и градиентного метода, метод секущих не требует вычисления производных. Этот метод также применяется для отыскания нулей функций. Если известны значения аргументов, при которых целевая функция принимает положительное и отрицательное значения, то очередной поиск согласно методу секущих следует делать на точке пересечения линии, проходящей через эти точки и оси нулевых значений. Значение целевой функции в новой точке по абсолютной величине предположительно будет меньше того значения, которое принимала целевая функция в исходной паре и имело тот же знак. Например, если имелись значения 100 и -50, то новое значение будет лежать внутри этого интервала, то есть будет положительной величиной менее 100 или отрицательной величиной более -50. В первом случае следует отбросить точку 100, во втором – точку -50, и новый поиск осуществлять на этом новом отрезке опять по методу секущих. Этим методом можно найти нулевое значение целевой функции. Для отыскания оптимальных значений параметров регулятора этот метод напрямую не пригоден.
Метод Розенброка
Метод Розенброка состоит в повороте осей поиска по результатам первых шагов метода покоординатного спуска. Новых оси получают поворотом старых осей. Положение новых осей может быть получено линейным преобразованием старых осей. Пусть имеется n аргументов целевой функции. После оптимизации по каждому из n аргументов получаем точку X n. В этой точке ни один из аргументов не совпадает со стартовым значением этой величины. После очередной процедуры оптимизации получаем точку X 2n. В этой точке ни одна из координат не совпадает с координатой из точки X n. Вектор X 2n - X n дает направление нового поиска, а ортогональные этому вектору другие векторы – направления дополнительных поисковых сканирований. Этот метод аналогичен развороту координат в таком направлении, чтобы первая координата по направлению совпала с линией оврага.
Метод Хука – Дживса
Метод Хука – Дживса является удачной модификацией метода покоординатного спуска. В соответствии с этим методом вначале выполняю серию из n шагов. Затем делают дополнительный шаг в направлении вектора X k – X k-n.
3.8.9. Метод Нелдера – Мида (деформируемого многогранника)
Если искомых параметров n, то следует строить многогранник с n + 1 вершиной. В частности при оптимизации по двум параметрам строится треугольник. Вначале вершины этого многогранника выбираются произвольно. Эти вершины следует ранжировать по величине целевой функции. Вершина с наибольшим значением (худшая) должна быть исключена в новом многограннике. Вычисляется точка центра тяжести многоугольника. В случае треугольника она лежит на точке пересечения медиан. Из худшей вершины через точку центра тяжести проводится луч, после пересечения этим лучом точки ЦТ откладывается отрезок такой же длины, как из худшей вершины до этой точки. Новая вершина заменяет худшую. Если оказывается, что новое значение целевой функции имеет самое лучше значение среди других вершин многогранника, то расстояние в этом направлении увеличивают, что дает новую точку. В новом многограннике опять отыскивается худшая вершина и метод повторяется заново.
3.8.10. Метод Флетчера-Рився (сопряженных градиентов)
Этот метод основан на понятии сопряженных векторов. Векторы A и B называют Q -сопряженными, если ATQB = 0, где Q – положительно определенная квадратная матрица того же порядка, что и размер N векторов A и B. Частный случай сопряженности – ортогональность векторов, когда Q – единичная матрица, A и B – вектор-столбцы. Более подробно с методом можно ознакомиться в [1, с.163].
Метод локальной оптимизации
Метод локальной оптимизации [1, с.182] предполагает при движении из каждой новой точки давать приращение по каждой координате отдельно, получать набор ближайших значений параметров, анализировать набор значений целевых функционалов, и двигаться в направлении минимального функционала из этого набора. В таком случае порядок начертания параметров регулятора не будет иметь значения, в этом смысле этот метод предпочтителен, поскольку движение идет преимущественно по той координате, по которой градиент целевого функционала существенней. ПРИМЕР 2. Получили регулятор после 5000 шагов [60/40/5]. После следующей итерации, например, получаем [60,5/40,2/5,1]. Изменения всех коэффициентов идут в одну сторону. Поэтому можно предположительно начать новую итерацию не с новых значений, а с тех, которые отличаются от старых на удвоенную величину полученных приращение, то есть [61/40,4/5,2]. ПРИМЕР 3. В тех же условиях, что и пример 2, после третьей итерации получаем [60,8/40,4/5,2]. Это говорит о том, что изменения коэффициентов идут монотонно, и в одном направлении, то есть мы достаточно далеки от экстремума. Скорее всего, следует повысить точность в настройках оптимизации, поскольку оптимизация, предположительно, завершается по признаку достаточно малого отличия полученного результата от истинного экстремума, то есть определена слишком грубая точность результата. Этот метод может привести к «застреванию» в точке локального экстремума. Повысить эффективность метода можно применением метода запретов, в соответствии с которым запрещено посещать ранее посещенные точки. В результате возникает тенденция к выходу из локальных экстремумов. Другой способ выхода из локальных экстремумов – по окончании процедуры оптимизации повторить ее с новыми стартовыми значениями. Для случая оптимизации ПИД-регуляторов, как минимум, можно попытаться увеличить все коэффициенты в 1,2 – 1,5 раза и уменьшить во столько же раз. Если каждый раз результат оптимизации будет тем же, можно надеяться, что результат является глобальным оптимумом. Для других задач изменения стартовых условий могут потребоваться существенно больше.
Эволюционные методы Генетический алгоритм
Генетический алгоритм – это подражание живой природе в методах решения технических задач. Хотя механизм эволюции не раскрыт, и не понят, имеется некая теория его действия, и этому действию м
|
||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.124.204 (0.016 с.) |

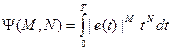 .
. .
.



