Другие соотношения в прямоугольном треугольнике

 

1) Устанавливая в предыдущем параграфе зависимость между сторонами прямоугольного треугольника, мы попутно вывели, что (черт. 206)

a2= bq,

c2= bp.

 

Выражая это соотношение словесно, мы скажем, что

к в а д р а т к а ж д о г о к а т е т а р а в е н п р о и з в е д е н и ю и з г и п о т е н у з ы и п р о е к ц и и э т о г о к а т е т а н а г и п о т е н у з у.

2) Кроме того, из подобия треугольников I и II следует, что

р: h= h: q, где h – высота,

т. е. h (высота) есть повторяющийся член непрерывной пропорции, другие члены которой есть р и q. Повторяющийся член непрерывной кратной пропорции принято называть средне-пропорциональным (или средне-геометрическим) между двумя остальными членами. Поэтому сейчас установленную зависимость можно высказать так:

в ы с о т а, п р о в е д е н н а я к г и п о т е н у з е, е с т ь с р е д н е – п р о п о р ц и о н а л ь н а я м е ж д у о т р е з к а м и г и п о т е н у з ы. Далее, из пропорции р: h = h: q следует, что h2 = pq, т. е.

к в а д р а т в ы с о т ы, п р о в е д е н н о й к г и п о т е н у з е, р а в е н п р о и з в е д е н и ю о т р е з к о в г и п о т е н у з ы.

 

Соотношения между отрезками перпендикулярных хорд

 

Проведем через: какую-нибудь точку окружности (черт. 208) перпендикуляр CD к диаметру АВ. Легко видеть, это этот перпендикуляр есть высота, проведенная к гипотенузе треугольника АСВ, так как угол АСВ – прямой (почему?). Поэтому

AD: DC = DC: DB,

или (DC)2= AD: DB;

 

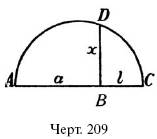
другими словами:

п е р п е н д и к у л я р, п р о в е д е н н ы й и з к а к о й – н и б у д ь т о ч к и о к р у ж н о с т и к д и а м е т р у, е с т ь с р е д н е – п р о п о р ц и он а л ь н о е м е ж д у о т р е з к а м и д и а м е т р а. Этим свойством можно пользоваться, между прочим, в тех случаях, когда требуется построить к двум данным отрезкам средне-пропорциональный. Если данные отрезки а и l и требуется найти отрезок х такой длины, чтобы

а: х = х: l,

то откладывают рядом а и l (черт. 209), строят на АС, как на диаметре, полуокружность и из точки В восставляют перпендикуляр до пересечения с окружностью в точке D: отрезок BD = x.

 

Повторительные вопросы к §§ 71–73

Какое вы знаете соотношение между катетами и гипотенузой? – Между гипотенузой, катетом и его проекцией на гипотенузу? – Между высотой, проведенной к гипотенузе, и отрезком гипотенузы? – Между перпендикуляром, проведенным из точки окружности к диаметру и отрезками диаметра? – Что значит: найти? средне-пропорциональное между двумя отрезками? Как это сделать?

Применения

91. Чтобы определить расстояние от точки В (черт. 210) до недоступной точки A провешивают прямую BN под прямым углом к направлению АВ и из произвольной точки С этой прямой провешивают CD перпендикулярно к направлению AC? Как, пользуясь этим построением, определить искомое расстояние АВ?

Р е ш е н и е. Надо измерить расстояния ВС и ВD. Расстояние АВ оп-редется из равенства:

(BC)2= AB?BD,

откуда

AB = (BC)2/ BD

92. Начертить квадрат, равновеликий данному треугольнику с основанием а высотою h.

Р е ш е н и е. Задача сводится к отысканию стороны квадрата такой длины х, чтобы x2 =? ah, т. е., чтобы a/2: х = х: h.

Отсюда видно, что искомый отрезок средне-пропорциональное между a/2 и h.

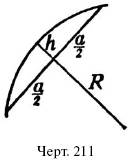
93. Найти стрелку h дуги (черт. 211) радиуса R, если длина стягивающей хорды = a.

Р е ш е н и е. Стрелкой дуги называется прилегающий к ней отрезок радиуса, перпендикулярного к стягивающей ее хорде, между хордой и дугой.

Половину хорды a/2 можно рассматривать, как перпендикуляр, проведенный из точки окружности к диаметру. Поэтому

( a/2 )2h?[2R-h], или: h2-2Rh + a2/4 = 0

Искомую величину стрелки h можно вычислить из этого квадратного уравнения. Если стрелка, как часто бывает, весьма мала по сравнению с радиусом круга, то членом h 2можно пренебречь, и тогда h приближенно равно a2/8R. По этой формуле вычисляют, например, стрелку дуги железнодорожного закругления, радиус которого достигает 1000 метров и больше, стрелка же не превышает нескольких, метров.

Сходным образом решается и обратная задача: вычисление радиуса закругления по длине хорды и стрелки, как видно из следующего примера.

94. Вычислить радиус кривизны часового стекла, поперечник которого 60 мм, а стрелка дуги – 3 мм.

Р е ш е н и е. Подставив значения a и h в уравнение, выведенное в предыдущем примере:

h2-2Rh + a2/4 = 0

получаем

0,32-2 R? 0,3 + 9 = 0.

Отсюда R = около 6 см.

 

Длина касательной

 

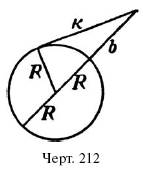
Пусть требуется определить длину касательной к (черт. 212), если радиус круга R, а кратчайшее расстояние от начала касательной до окружности – b. Проведя радиус к точке касания, имеем прямоугольный треугольник, в котором

[ b + R ]2= R 2+ k 2.

Раскрыв скобки, получаем

b 2+ 2 bR + R 2= R 2+ k 2.

Отсюда

k 2= b 2+ 2 bR = b [ b + 2 R 2].

 

 

Это соотношение можно выразить словесно так:

к в а д р а т к а с а т е л ь н о й р а в е н п р о и з в е д е н и ю в с е й т е к у щ е й, п р о в е д е н н о й и з н а ч а л а к а с а т е л ь н о й ч е р е з ц е н т р, н а в н е ш н и й о т р е з о к э т о й с е к у щ е й.

Применения

95. Как далеко можно видеть в море с маяка высотою 30 метров?

Р е ш е н и е. Так как поверхность моря шарообразна, то дальность видимости определяется длиной касательной, проведенной из верхушки маяка к кругу, радиус которого равен радиусу земного шара (6400 км). Поэтому искомая даль-ность х определяется из равенства

x 2= 30 [12 800 000 + 30].

(Слагаемым 30 в данном случае можно пренебречь). Получаем х = около 20 км.

96. Как высоко должен подняться летчик, чтобы видеть за 200 километров?

Р е ш е н и е. В этом случае, в отличие от предыдущего, известна длина касательной, и ищется внешний отрезок секущей, проходящей через центр круга радиус которого 6400 км. Поэтому искомая высота у определяется из уравнения

2002= у [12 800 + y ].

Слагаемое у, очевидно, весьма мало по сравнению с диаметром земного шара. Пренебрегая им, имеем

2002= 12 800 у,

Откуда

2002/12800 = 2,3 км.

Следовательно, искомая высота = 23 км.