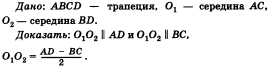Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Окружность, описанная около треугольника.Содержание книги
Поиск на нашем сайте Окружность называется описанной около треугольника, если она проходит через все его вершины.
Задача по теме «Сумма углов треугольника».
Задача по теме «Трапеция». Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям трапеции и равен полуразности оснований.
Построение с помощью циркуля и линейки треугольника по трем сторонам. Построение (рис. 32). «Пусть а — большая из трех сторон. Возьмем произвольный луч с началом С и проведем окружность радиуса а с центром в точке С.
Сложение векторов. Свойства сложения векторов.
Задача по теме «Многоугольники». Сколько сторон имеет выпуклый многоугольник, если все его внешние углы тупые?
Умножение вектора на число. Свойство произведения вектора на число.
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 577; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.008 с.) |