Задача по теме «Равнобедренный треугольник».

На боковых сторонах равнобедренного треугольника во внешнюю сторону построены равносторонние треугольники. Докажите, что отрезки, соединяющие вершины равносторонних треугольников (отличные от вершин равнобедренных треугольников) с серединой основания равнобедренного треугольника, равны.

 

 

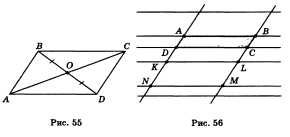
53. Свойство параллелограмма (формулировки и примеры).

I. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

II. В параллелограмме противолежащие стороны равны и противолежащие углы равны.

Примеры.

1. В параллелограмме ABCD диагональ BD равна 12 см, О — точка пересечения диагоналей параллелограмма. Чему равен отрезок DO (рис. 55)?

Решение. По свойству диагоналей параллелограмма

2. В параллелограмме ABCD постройте медиану A BCD, проходящую через вершину С.

Построение. Проведем диагональ АС. Она пересекает диагональ BD в точке О. Так как диагонали параллелограмма в точке пересечения делятся пополам, то ВО = OD, значит, СО — медиана ABCD.

3. В параллелограмме сумма двух углов равна 132°. Найдите градусную меру каждого из этих углов.

Решение. Два данных угла не могут быть прилежащими к одной стороне, так как в этом случае их сумма была бы равна 180°: Значит, эти углы противолежащие. По свойству противолежащих углов параллелограмма они равны и каждый из них равен 66°.

4. На рисунке 56 приведен фрагмент страницы тетради в косую линейку. Отрезок АВ равен 3 см, а наклонные линии образуют с горизонтальными



угол, равный 60°. Найдите стороны KL и NM и углы ячейки KLMN.

Решение. По определению параллелограмма все ячейки страницы тетради в косую линейку являются параллелограммами, так как все горизонтальные линии параллельны и все наклонные линии параллельны.

По свойству сторон параллелограмма АВ = DC (из параллелограмма ABCD), DC = KL (из параллелограмма DCLK), KL = NM (из параллелограмма KLMN).

Отсюда АВ = DC = KL = NM = 3 см. Углы KNM и KLM параллелограмма KLMN равны по свойству противолежащих углов параллелограмма и равны 60° по условию. Так как углы NKL и KNM — прилежащие к одной стороне параллелограмма, то

 

 

Теорема о внешнем угле треугольника.

Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.

Чтобы не путать угол треугольника при данной вершине с внешним углом треугольника при этой же вершине, его иногда называют внутренним углом.

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.



Отсюда следует, что , т. е. внешний угол при вершине равен сумме углов А и В, что и требовалось доказать.

Отсюда следует, что внешний угол треугольника больше любого внутреннего угла, не смежного с ним.

 

 

Задача по теме «Признаки равенства треугольников».

 

 

Задача по теме «Площадь».

 

 

57. Теорема о средней линии трапеции (формулировка и пример).

Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.

Пример.

 

 

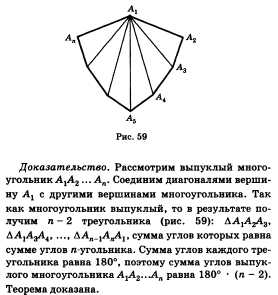
Теорема о сумме углов выпуклого многоугольника.

Многоугольник называется выпуклым, если он

лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.

Сумма углов выпуклого п-угольника равна 180° - (п - 2).

 

 

Задача по теме «Признаки равенства треугольников».

 

 

Задача по теме «Решение прямоугольных треугольников».

 

 

61. Формулы для радиусов вписанных и описанных окружностей правильного n-угольника (формулы и примеры).

 

 

Свойство диагоналей ромба.

Дано: ABCD — ромб, АС и BD — диагонали, О — точка пересечения диагоналей.

Доказать: AC BD, АС и BD — биссектрисы углов ромба.

Доказательство. Рассмотрим ромб ABCD (см. рис. 61). По свойству параллелограмма АО = ОС. Значит, в треугольнике ABC отрезок ВО является медианой. Так как ABCD — ромб, то АВ = ВС и треугольник ABC — равнобедренный. По свойству равнобедренного треугольника медиана, проведенная к его основанию, является биссектрисой и высотой. А это значит, что диагональ BD является биссектрисой угла В и перпендикулярна диагонали АС. Аналогично рассматривается AABD. Теорема доказана.

 

 

Задача по теме «Равнобедренный треугольник».