
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача по теме «подобие треугольников».Содержание книги
Поиск на нашем сайте
65. Формулы для радиусов вписанных и описанных окружностей правильного треугольника, правильного четырехугольника, правильного шестиугольника (формулы и примеры).
Свойство диагоналей прямоугольника. Прямоугольник — это параллелограмм, у которого все углы прямые (рис. 62).
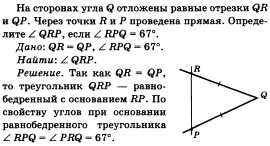
Задача по теме «Равнобедренный треугольник».
Задача по теме «Параллельные прямые».
Первый признак равенства треугольников. [П] Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Задача по теме «Площадь». ABCD — трапеция. Докажите, что треугольники ABD и ACD имеют равные площади.
Задача по теме «Многоугольники».
72. Формулы площади треугольника (формулы и примеры).
Признак параллелограмма. Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны, т. е. лежат на параллельных прямых.
Задача по теме «Равнобедренный треугольник».
Задача по теме «Углы, вписанные в окружность».
76. Формулы площади прямоугольника и параллелограмма (формулы и примеры). I. Площадь прямоугольника со сторонами а и b равна произведению их сторон S = аЬ.
Второй признак равенства треугольников.
Задача по теме «Средняя линия треугольника».
79. Формула площади трапеции (формула и пример).
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.008 с.) |









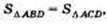
 , что и требовалось доказать.
, что и требовалось доказать.
















