
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение треугольника по стороне и двум углам.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ответы по геометрии для 9 класса
1. Признаки параллельности прямых (формулировки и примеры). Решение треугольника по стороне и двум углам. Задача по теме «Углы, вписанные в окружность». Задача по теме «Длина окружности». 5. Свойство углов, образованных при пересечении двух параллельных прямых третьей прямой (формулировки и примеры). Решение треугольника по двум сторонам и углу между ними. Задача по теме «Неравенство треугольника». 8. Третий признак равенства треугольников (формулировка и пример). Теорема об углах, вписанных в окружность. Задача по теме «Площадь». Задача по теме «Трапеция». 12. Теорема о сумме углов треугольника (формулировка и пример). Решение треугольника по трем сторонам. Задача по теме «Средняя линия трапеции». Определение синуса острого угла прямоугольного треугольника. Пример его применения для решения прямоугольных треугольников. Свойство углов равнобедренного треугольника. Задача по теме «Подобие треугольников». Задача по теме «Параллелограмм». Определение косинуса острого угла прямоугольного треугольника. Пример его применения для решения прямоугольных треугольников. Признак равнобедренного треугольника. Задача по теме «Подобие треугольников». Задача по теме «Прямоугольник». Определение тангенса острого угла прямоугольного треугольника. Пример его применения для решения прямоугольных треугольников. Свойство медианы равнобедренного треугольника. Задача по теме «Подобие треугольников». Задача по теме «Ромб. Квадрат». Теорема косинусов. Пример ее применения для решения треугольников. Окружность, вписанная в треугольник. Задача по теме «Параллельные прямые». Задача по теме «Теорема Пифагора». Теорема синусов. Пример ее применения для решения треугольников. Окружность, описанная около треугольника. Задача по теме «Сумма углов треугольника». Задача по теме «Трапеция». Построение с помощью циркуля и линейки треугольника по трем сторонам. Сложение векторов. Свойства сложения векторов. Задача по теме «Многоугольники». Умножение вектора на число. Свойство произведения вектора на число. Задача по теме «Многоугольники». 40. Задача по теме «Свойства прямоугольного треугольника, у которого один угол равен 30°». Построение с помощью циркуля и линейки биссектрисы угла. Неравенство треугольника. Задача по теме «Параллелограмм». Задача по теме «Углы, вписанные в окружность». Построение с помощью циркуля и линейки перпендикулярной прямой. Признаки подобия треугольников (доказательство одного из них). Задача по теме «Прямоугольник». Задача по теме «Углы, вписанные в окружность». Деление отрезка пополам с помощью циркуля и линейки. Теорема о средней линии треугольника. Задача по теме «Ромб. Квадрат». Задача по теме «Равнобедренный треугольник». 53. Свойство параллелограмма (формулировки и примеры). Теорема о внешнем угле треугольника. Задача по теме «Признаки равенства треугольников». Задача по теме «Площадь». 57. Теорема о средней линии трапеции (формулировка и пример). Теорема о сумме углов выпуклого многоугольника. Задача по теме «Признаки равенства треугольников». Задача по теме «Решение прямоугольных треугольников». 61. Формулы для радиусов вписанных и описанных окружностей правильного n-угольника (формулы и примеры). Свойство диагоналей ромба. Задача по теме «Равнобедренный треугольник». Задача по теме «Подобие треугольников». 65. Формулы для радиусов вписанных и описанных окружностей правильного треугольника, правильного четырехугольника, правильного шестиугольника (формулы и примеры). Свойство диагоналей прямоугольника. Задача по теме «Равнобедренный треугольник». Задача по теме «Параллельные прямые». Первый признак равенства треугольников. Задача по теме «Площадь». Задача по теме «Многоугольники». 72. Формулы площади треугольника (формулы и примеры). Признак параллелограмма. Задача по теме «Равнобедренный треугольник». Задача по теме «Углы, вписанные в окружность». 76. Формулы площади прямоугольника и параллелограмма (формулы и примеры). Второй признак равенства треугольников. Задача по теме «Средняя линия треугольника». 79. Формула площади трапеции (формула и пример). Признак равенства прямоугольных треугольников. Задача по теме «Векторы». Задача по теме «Окружность, вписанная в треугольник». 83. Формула площади круга (формула и пример). Теорема Пифагора. Задача по теме «Окружность, описанная около треугольника». Решение треугольника по стороне и двум углам. Решить треугольник по стороне и двум прилежащим к ней углам — это значит при заданных стороне и двум прилежащим к ней углам найти третий угол и две другие стороны.
Задача по теме «Площадь». Найдите площадь ромба, если его диагонали равны 6 см и 8 см.
Задача по теме «Трапеция».
12. Теорема о сумме углов треугольника (формулировка и пример). Примеры.
Определение синуса острого угла прямоугольного треугольника. Пример его применения для решения прямоугольных треугольников. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
Определение косинуса острого угла прямоугольного треугольника. Пример его применения для решения прямоугольных треугольников. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
Определение тангенса острого угла прямоугольного треугольника. Пример его применения для решения прямоугольных треугольников. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего
Теорема косинусов. Пример ее применения для решения треугольников. Квадрат любой стороны треугольника равен сумме квадратов катетов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Теорема синусов. Пример ее применения для решения треугольников. Стороны треугольника пропорциональны синусам противолежащих углов (рис. 29):
Задача по теме «Трапеция». Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям трапеции и равен полуразности оснований.
Неравенство треугольника. Если точки А и В различны, то расстоянием между ними называется длина отрезка АВ. Если точки А и В совпадают, то расстояние между ними принимается равным нулю.
Задача по теме «Площадь».
57. Теорема о средней линии трапеции (формулировка и пример). Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.
Свойство диагоналей ромба.
Задача по теме «Площадь». ABCD — трапеция. Докажите, что треугольники ABD и ACD имеют равные площади.
Признак параллелограмма. Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны, т. е. лежат на параллельных прямых.
Задача по теме «Векторы».
Теорема Пифагора.
Ответы по геометрии для 9 класса
1. Признаки параллельности прямых (формулировки и примеры). Решение треугольника по стороне и двум углам.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 604; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.51.72 (0.011 с.) |









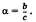









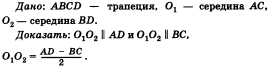







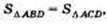
 , что и требовалось доказать.
, что и требовалось доказать.






