VIII. Дополнительные сведения о треугольниках

 

Равнобедренный треугольник

 

С основными свойствами всякого треугольника мы познакомились в §§ 15–22. Самые главные из них следующие: сумма углов треугольника равна 180°; треугольники равны друг другу или по трем сторонам, или по двум сторонам и углу между ними, или по одной стороне и двум углам (для краткости мы обозначили эти случаи так: ССС, СУС, УСУ). Теперь познакомимся с некоторыми новыми свойствами треугольников.

Предварительные упражнения

Укажите равные треугольники в фигуре черт. 134, где АВ = АС, a AD – равноделящая угла А.

Каковы углы ADB и ADС на черт. 134: острые или тупые?

Мы знаем, что в р а в н ы х треугольниках против равных сторон лежат равные углы. Покажем, что и

в о д н о м и т о м ж е т р е у г о л ь н и к е п р о т и в р а в н ы х с т о р о н л е ж а т р а в н ы е у г л ы.

 

Пусть у нас взят треугольник ABC (черт. 135), в котором сторона АВ равна стороне АС. Легко убедиться, что в таком треугольнике углы В и С, лежащие против равных сторон, равны между собой. Если в нашем треугольнике проведем (черт. 136) равноделящую АD угла А, она разобьет ABC на два треугольника: АDB и АDС, которые равны между собой (СУС). По этому угол В, лежащий против AD, равен углу С, лежащему против той же общей стороны.

Треугольник с двумя равными сторонами называетс я р а в н о б е д р е н н ы м; его равнее стороны называются б о к о в ы м и с т о р о н а м и этого треугольника, а третья сторона – его о с н о в а н и е м.

Поэтому рассмотренное сейчас свойство треугольника можно высказать короче так:

в р а в н о б е д р е н н о м т р е у г о л ь н и к е у гл ы п р и о с н о в а н и и р а в н ы.

Можно удостовериться и в обратном соотношении: если в треугольнике имеются равные углы, то стороны, лежащие против этих углов, – равны; или-короче сказать:

в т р е у г о л ь н и к е п р о т и в р а в н ы х у г л о в л е ж а т р а в н ы е с т о р о н ы.

 

Чтобы убедиться в этом, возьмем треугольник (черт. 135), в котором два угла равны: уг. B = уг. C. Проведем (черт. 136) равноделящую AD; в образовавшихся двух треугольниках ADB и ADC сторона AD – общая, уг. BAD = уг. CAD, уг. В = уг. C; следовательно, треугольники равны (УСУ), и потому АВ = АС.

Применения

52. Огород имеет форму равнобедренного треугольника, одна сторона которого на 40 м длиннее другой. Обвод огорода 200 м. Какова длина каждой стороны? Сколько решений имеет эта задача?

Р е ш е н и е. Если оcнование этого треуголь ника больше боковых сторон, то, обозначив его через х, имеем уравнение

х + х – 40 + х – 40 = 200,

из которого находим: х =280/3 = 93 1/3 м.

Значит, в таком случае стороны треугольника имеют длину: 93 1/3 м, 531/3 м и 531/3 м.

Если же основание к о р о ч е боковых сторон, то составляем уравнение

y + y + 40 + y + 40 = 200,

из которого y = 40 м. Следовательно, второе решение задачи 40 м, 80 м и 80 м.

 

53. Кровля, в зависимости от материала, из которого она сделана, должна составлять с горизонтальной линией следующие углы (черт. 137):

Железная и цинковая... 30°

Толевая.......... 18°

Черепичная........ 40°

Тесовая.......... 45°

Соломенная........ 60°

Зная это, определите, какой угол должны составлять между собой стропильные ноги двускатной крыши в каждом случае.

Р е ш е н и е. Для железной кровли искомый угол равен 180° – 2? 300 = 120°; для толевой 180° – 2? 18° = 144°; для черепичной 180° – 2? 40° = 100°; для тесовой 180° – 2? 45° = 90°; для соломенной 180° – 2? 60° = 60°.

 

Угол, опирающийся на диаметр

 

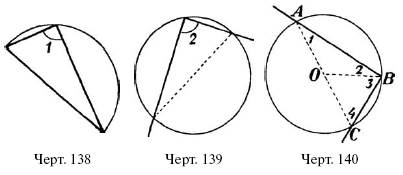
Из свойств равнобедренного треугольника вытекает следующая особенность угла, вписанного в полукруг (черт. 138) или: как его иначе называют – «опирающего на диаметр»:

 

У г о л, о п и р а ю щ и й с я н а д и а м е т р, р а в е н п р я м о м у.

 

«Опирающимся на диаметр», или «вписанным в полукруг» называют такой угол, вершина которого лежит на дуге окружности, а стороны проходят через концы диаметра; таковы углы: 1 на черт. 138 и 2 на черт. 139. Желая удостовериться, что такой угол во всех случаях равен 90°, мы соединяем центр О полукруга (черт. 140) с вершиной В угла. Получаем два равнобедренных треугольника АОВ и ВОС (почему они равнобедренные?). В них

уг. 2 = уг. 1

уг. 3 = уг. 4.

 

Отсюда уг. 2 + уг. 3 (т. е. уг. АВС) = уг. 1 + уг. 4. Но так как уг. АВС + уг. 1 + уг. 4 = 180°, то уг. ABC = 90°.

Этим свойством окружности пользуются нередко для того, чтобы в изделиях проверять полуокружность помощью чертежного треугольника (как?).

 

Прямоугольный треугольник

 

В треугольнике, мы знаем, может быть только один прямой угол. Такой треугольник называется п р я м о у г о л ь н ы м. Стороны прямоугольного треугольника имеют особые названия: каждая из сторон, между которыми лежит прямой угол, называется к а т е т о м, а сторона против прямого угла называется г и п о т е-н у з о й.

Применения

54. Через точку С (черт. 141) на прямой MN нужно провести перпендикуляр. Как это сделать?

Р е ш е н и е. Отложив (черт. 142) от С в обе стороны по какому-нибудь равному отрезку, т. е. CA = CB, описываем около А и В, как центров, каким-нибудь радиусом дуги; прямая PC, соединяющая точку Р пересечения дуг с точкой С, перпендикулярна к МN. Действительно, треугольники АР С и ВРС, получающиеся после соединения А и В с P, равны (СУС); следовательно, уг. АСР = уг. ВСР, а так как эти углы смежные, то они – прямые.

55. Через точку С (черт. 143) вне прямой МN про вести к этой прямой перпендикуляр.

Р е ш е н и е. Около точки С, как около центра, описываем каким-нибудь радиусом дугу АВ (черт. 144);

 

затем около точек А и В каким-нибудь радиусом описываем дуги D. Прямая DС перпендикулярна к МN. Чтобы убедиться в этом, соединим С и D с А и В.

Треугольники ACD и ВCD равны (ССС), следовательно, уг. ACD = уг. DCВ, и значит, треугольник АСО = ВСО (СУС). Отсюда уг. AОС = уг. ВОС, а так как эти углы смежные, то они прямые.

 

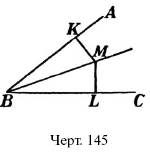
56. Объясните, почему каждая точка М прямой ВM, делящей пополам угол АВС (черт. 145) одинаково отстоит от сторон АВ и ВС угла (т. е. почему, например, MK = ML?).

Р е ш е н и е. Треугольники ВML и ВМК равны (УСУ).

 

Равносторонний треугольник

 

Треугольник с тремя равными сторонами называется р а в н о с т о р о н н и м. Так как против равных сторон в одном и том же треугольнике лежат равные углы, то все углы равностороннего треугольника равны, и, следовательно, каждый из них равен. 180°: 3 = 60°.

Обратно: если каждый угол треугольника равен 60°, то все стороны такого треугольника одинаковы, – потому что, против равных углов в одном и том же треугольнике лежат, равные стороны.

Применения

57. Без транспортира построить угол в 60°. В 30°. В 15°. В 120°. В 75°.

Р е ш е н и е. Строим равносторонний треугольник произвольных размеров; каждый его угол = 60°. Разделив угол этого треугольника пополам, получим угол в 30°. Разделив еще раз пополам, будем иметь угол в 15°. Угол в 120° = 90° + 30°. Угол в 75° =60° + 15° = 90° – 15°.

 

§ 52. Катет против угла в 30°

 

Предварительное упражнение

Равносторонний треугольник разбит равноделящей одного из углов на два треугольника. Определить их углы.

уг. D = 60°; а так как и уг. ABD = 60°, то треугольник ABD – равносторонний, и следовательно, AD = АВ. Но АС = 1/2 АD (почему?); отсюда АС = 1/2 АВ.

 

Итак, мы убедились, что

к а т е т п р о т и в у г л а в 30° р а в е н п о л о в и н е г и п о т е н у з ы.

Применения

58. Лестница длиною 6 м приставлена к фонарному столбу под углом 30° к нему (черт 148). Каково расстояние от основания лестницы до основания фонаря?

Р е ш е н и е. Так как катет против 30° равен половине гипотенузы, то искомое расстояние = 3 м.

59. Длина стропильной ноги АС (черт. 137) вдвое больше высоты AD стропильной фермы. Определить угол наклона этой кровли к горизонту.

Р е ш е н и е. Искомый угол СAD = 30°, так как только при таком условии CD равно половине АС.

Пусть у нас имеется прямоугольный треугольник (черт. 146) ABC, один угол которого, именно В, равен 30°. Перегнем мысленно треугольник по катету ВС. Тогда займет положение ВСD (черт. 147), при чем CD составит продолжение АС, потому что уг. ВСD + ВСА = развернутому. Уг. СВD = уг. ABC = 30°; значит, уг. А = 60°;

 

Неравные стороны и углы

 

Мы знаем, что если в треугольнике есть равные стороны, то углы, лежащие против них, тоже равны. Рассмотрим теперь, каково соотношение между сторонами и углами в случае н е р а в н ы х сторон.

 

Предварительное упражнение

В фигуре черт. 149 укажите какой угол больше: уг. 1 или у г. 2?

В фигуре черт. 151 АВ = AD. Какой угол больше; уг. С или у г. 1?

Покажем, что в

т р е у г о л ь н и к е с н е р а в н ы м и с т о р о н а м и п р о т и в б о л ь ш е й с т о р о н ы л е ж и т б о л ь ш и й у г о л. Пусть в треугольнике АВС (черт. 150) сторона АС больше «стороны АВ. Отложим от вершины образуемого ими угла меньшую сторону АВ на большей АС получим точку D. Соединив D с В, имеем равнобедренный треугольник ABD, в котором угол 1 = уг. 2. Угол С меньше угла 1, а значить, подавно меньше угла. ABC. Таким образом мы убеждаемся, что против большей стороны [АС] лежит больший угол [ABC].

Нетрудно удостовериться, что и обратно: если в треугольнике имеются неравные углы, то

п р о т и в б о л ь ш е г о у г л а л е ж и т б о л ь ш а я с т о р о н а.

 

Пусть мы знаем, что в треугольнике (черт. 151) ABC уг. А больше угла С. Тогда сторона ВС не может быть равна АВ: иначе уг. А равнялся бы углу С; не может сторона ВС быть и м е н ь ш е: АВ – тогда уг. А был бы м е н ь ш е угла С (а мы знаем, что уг. А б о л ь ш е уг. С). Не равен и не меньше, значит – больше.

Применения

60. Что больше: гипотенуза или катет?

Р е ш е н и е. Гипотенуза, как сторона, лежащая против самого большого угла треугольника, длиннее каждого катета.

61. Угол при вершине равнобедренного треугольника = 70°. Что длиннее: основание или боковая сторона?

Р е ш е н и е. Углы при основании равны (180°-70°) / 2 = 65°.

Так как угол прш вершине больше, то основание больше боковых сторон.

Повторительные вопросы к §§ 48–53

Каково соотношение между углами треугольника, две стороны которого равны? – каково соотношение между сторонами треугольника, имеющего два равных угла? – Каковы соотношения в треугольнике с неравными сторонами? – С нерав-нымиуглами? – Какой треугольник называется равнобедренным? – Какая сторона такого треугольника называется боковой? – Какая называется основанием? – Как называется треугольник, имеющий два равных угла? – Сколько градусов в угле, опирающемся на диаметр? – Какой треугольник называется прямоугольным? – Что называется гипотенузой? – Катетами? – По каким признакам можно установить равенство прямоугольных треугольников? – Какой треугольник называется равносторонним? – Как велики его углы? – Каково соотношение между гипотенузой и катетом, лежащим против угла в 1/3 прямого?