
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: подобие треугольников.Содержание книги Поиск на нашем сайте
Теоретическая часть Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне. D BC A KLM Теорема о пропорциональных отрезках. Если параллельные прямые, пересекающие стороны угла, то отрезки образованные на одной стороне угла, пропорциональны соответствующим отрезкам, образовавшемся на другой стороне угла. Т.е. если BK || CL || DM, то Определение. Два треугольника называются подобным, если их углы соответственно равны и стороны одного треугольника пропорциональны сторонам другого треугольника.
Признаки подобия треугольников
Практическая часть 1. Начертите произвольный отрезок и разделите его на семь равных частей. 2. На рисунке 1 ВD || СЕ, АВ =16 см, ВС = 6 см, АD = 8 см. Найдите отрезок DЕ. B 6 C 16 A рис.1 8 D E 3. Прямая, парaллельнаястороне ВС треугольника АВС, пересекает его сторону АВ в точке М, а сторону АС -в точке К. АМ = 9 см, ВМ = 6 см, КС = 8 см.Найдите отрезок АК. 4. Стороны МК и DЕ КТ и EF — соответственные стороны подобных треугольников МКТ и DEF, МК = 18 см, КТ = 16 см, МТ = 28 см, МК: DЕ =4:5. Найдите стороны треугольника DЕF. 5. На стороне СD параллелограмма АВСD отмечена точка Е, прямые ВЕ и АD пересекаются в точке F, СЕ = 8см, DE = 4см, ВЕ = 10см, АD = 9см. Найдите длину отрезков EF и FD. BC E А DF D 6. Угол между боковой стороной и основанием одного равнобедренного треугольника равен углу между боковой стороной и основанием другого равнобедренного треугольника. Боковая сторона и основание первого треугольника равны 18 см и 10 см соответственно, а основание второго — 8 см. Найдите боковую сторону второго треугольника.
7. Стороны параллелограмма равны 20 см и 14 см, высота, проведённая к большей стороне, равна 7 см. Найдите высоту параллелограмма, проведённую к меньшей стороне. DE BC 5 4 А 8..Известно, что ВС перпендикулярно АЕ, ВА = 5, АС = 4, СЕ = 6.Найдите DE?
9.Отрезки АВ и СD пересекаются в точке О, АО = 24 см, ВО = 16 см, СО = 15 см, ОD= 10 см, <АСО = 72°.Найдите <ВDО. C В
O AD 10. На сторонах АС и ВС треугольника АВС отметили соответственно точки М и К так, что СМ = 15 см, СК -12 см. Найдите МК, если АС = 20 см, ВС = 25 см, АВ = 30 см.
В D
А С 11. ΔАВС, ΔАВD, ΔАDC – прямоугольные. Докажите, что ΔАВС ≈ ΔАВD ≈ ΔАDC. Тема: Cоотношения между сторонами и углами в прямоугольном треугольнике. Теоретическая часть
c b a Таблица значений синуса, косинуса и тангенса.
Практическая часть
1. Сторона прямоугольника равна 8см, а диагональ – 10см. Найдите соседнюю к исходной сторону прямоугольника. Замечание: Треугольник с соотношением сторон 3: 4: 5 называется египетским.
2. Высота равнобедренного треугольника, проведённая к основанию, равна 35см, а его основание – 24см. Чему равна боковая сторона треугольника?
3. Сторона ромба равна 26см, а одна из диагоналей - 48см. Найдите другую диагональ ромба.
4. Гипотенуза прямоугольного треугольника равна 15см, а катеты относятся 4: 3. Найдите катеты этого треугольника.
5. В ΔАВС известно, что АВ = 17см, ВС = 9см, <С – тупой, высота АD = 8cм. Найдите сторону АС.
6. Найдите диагональ квадрата со стороной а.
7. Катеты прямоугольного треугольника равны 3см и 2см. Найдите: А) тангенс угла, прилежащего к большему катету; Б) синус угла, противолежащего меньшему катету; В) косинус угла, прилежащего к большему катету;
8. Найдите значение выражения:
9. В ΔАВС известно, что<С = 90°, ВС = 41см, АС = 20см. Найдите косинусы острых углов треугольника.
10. Найдите
11. Боковая сторона равнобедренного треугольника равна 17см, а высота, проведённая к основанию - 8см. Найдите синус, косинус и тангенс угла при основании треугольника.
12. Гипотенуза прямоугольного треугольника равна 10см, а косинус одного из острых углов равен 0,8. Найдите катеты треугольника. 13. В прямоугольном треугольнике один из катетов равен 12 см, а тангенс прилежащего угла — 0,75. Найдите второй катет и гипотенузу треугольника.
14. Какой должна быть пожарная лестница, чтобы по ней можно было подняться на крышу дома, высотой 9м, если ставить ее под углом 60° к поверхности земли?
15. Основания равнобедренной трапеции равны 8 см и 12 см, а угол при основании - 45°. Найдите высоту и боковую сторону трапеции. Список литературы. 1. Алимов Ш.А., Колягин Ю.М. Алгебра 7. – М. «Просвещение» 2010. 2. Алимов Ш.А., Колягин Ю.М. Алгебра 8. – М. «Просвещение» 2010. 3. Атанасян Л.С. Геометрия 7 – 9. М. «Просвещение» 2010. 4. Мерзляк Г.А. Геометрия 7.-М. «Вентана-Граф» 2013. 5. Мерзляк Г.А. Геометрия 8.-М. «Вентана-Граф» 2013. 6. Мерзляк Г.А. Сборник задач и заданий для тематического оценивания по алгебре для 7 класса. Харьков. «Гимназия» 2010. 7. Мерзляк Г.А. Сборник задач и заданий для тематического оценивания по геометрии для 7 класса. Харьков. «Гимназия» 2010. 8. Мерзляк Г.А. Сборник задач и заданий для тематического оценивания по алгебре для 8 класса. Харьков. «Гимназия» 2010. 9. Мерзляк Г.А. Сборник задач и заданий для тематического оценивания по геометрии для 8 класса. Харьков. «Гимназия» 2010.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 632; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.40.234 (0.008 с.) |

 .
. +
+  = 1.
= 1.
 =
=  ,
,  =
=  ,
,  =
=  =
= 


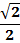








 -
-  .
. , если
, если  .
.


