
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тригонометрические функции острого угла прямоугольного треугольника.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гл.VII, §4. п.66. Сдать до 27.03.2016 Письменно ответьте на вопросы: А) Что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника? Б) Запишите основное тригонометрическое тождество.
1. Катеты прямоугольного треугольника равны 3см и 2см. Найдите: А) тангенс угла, прилежащего к большему катету; Б) синус угла, противолежащего меньшему катету; В) косинус угла, прилежащего к большему катету; Г) котангенс угла, противолежащего большему катету.
2. Заполните таблицу.
3. Найдите значение выражения:
4. В ΔАВС известно, что<С = 90°, ВС = 41см, АС = 20см. Найдите косинусы острых углов треугольника. 5. Найдите 6. Боковая сторона равнобедренного треугольника равна 17см, а высота, проведённая к основанию - 8см. Найдите синус, косинус, тангенс и котангенсугла при основании треугольника.
7*. Найдите углы между диагональю прямоугольника и его сторонами, длины которых В трапеции АВСD известно, что ВСǁAD, <A = 90°, АВ = 4см, ВС = 8см, АD = 12см,. Найдите углы трапеции. Диагностическая контрольная работа № 1
Образовательный минимум по алгебре 8 класс. Тема: Арифметический квадратный корень. Теоретическая часть Т.к. 32 = 9 и (-3)2 = 9, то числа 3 и -3 называются квадратными корнями числа 9. Т.о. любое неотрицательное число a имеет два корня (неотрицательный и отрицательный). Исключение: 0 – единственный корень из числа 0. Неотрицательный корень из числа a называют ещё арифметическим квадратным корнем, и обозначают Пример: квадратными корнями числа 17 будут Свойства арифметического квадратного корня.
Таблица квадратов чисел от 11 до 25.
Числовые множества.
 , где m – целое число, , где m – целое число,а n – натуральное; или конечной десятичной, или бесконечной периодической десятичной дробью. Пр: - Иррациональные числа (I) – бесконечныедесятичные непериодические дроби. Пр. число Действительные числа (R) – это рациональные и иррациональные числа вместе.
Практическая часть. 1. 2.
3. Вычислить:
4. Сравнить числа: 1) 7 и 5. 6. 7. 8. 9. Упростите выражение: 10.
Тема: Квадратные уравнения Теоретическая часть Уравнение вида ах2 + вх + с = 0, где а (а ≠ 0), в, с некоторые действительные числа, называется квадратным.
Практическая часть.
Тема: Квадратичная функция Определение. Функция вида y = ax2 + bx + c, где a,b и с – действительные числа (а ǂ 0), x, y – переменные величины, называется квадратичной функцией. График квадратичной функции (парабола). 1) Функция у = х2. 2) Функция у = ах2.
Основные свойства функции у = ах2 1) Если а > 0, то функция при (х ǂ 0) принимает положительные значения (а > 0, ветви вверх), если а < 0, то функция при (х ǂ 0) принимает отрицательные значения (а < 0 ветви вниз); 2) Функция у = ах2 симметрична относительно оси у; 3) Если а > 0, то функция у = ах2возрастает при х ≥ 0 и убывает при х ≤ 0, если а < 0, то функция у = ах2убывает при х ≥ 0 и возрастает при х ≤ 0.
Построение графика функции y = ax2 + bx + c. 1) Строим вершину параболы (х0, у0), вычислив х0, у0 по формулам
2) Проводим через вершину параболы ось симметрии – прямую параллельную оси ординат; 3) Решаем уравнение ax2 + bx + c = 0 и находим его корни х1, х2 – точки пересечения графика функции с осью абсцисс (нули функции). 4) Подставив в формулу y = ax2 + bx + c вместо х значение х = 0, находим точку пересечения графика функции с осью ординат. Определение. Наибольшим (наименьшим) значением функции у = f(x) на промежутке [а; b] – называется такое значение функции, при котором она достигает своего наибольшего (наименьшего) значения. Практическая часть 1. По точкам построить график функции у = х2. По графику найти приближенные значения а) значение у при х = 1,5, х = -1,5, х = 3; б) значение х при у = 3, у = 0, у = -3. 2. Найти координаты точек пересечения параболы у = 3х2 и прямой двумя способами: графически и решив систему уравнений: а) у = 6; б) у = 3 – 2х. 3. Найти координаты вершины параболы: а) у = 2х2 – 6х + 11; б) у = -3х2 + 18х – 7; в) у = -х2 – 5; г) у = -4х2 + х. 4. Найти координаты точек пересечения параболы с осями координат: а) у = х2 – 3х + 2; б) у = -2х2 + 3х – 1; в) у = 3х2 – х. 5. На одной системе координат, используя преобразования графиков, построить графики функций: а) y = x2; б) y = (x – 2)2; в) y = (x – 2)2 + 3; г) y = 2x2; д) y = - 2x2. 6. Принадлежит ли точка (1; -6) параболе у = -3х2 + 4х – 7? 7. Построить график функции: а) у = х2 +4х + 5; б) у = -х2 + 6х – 9; в) у = 2х2 – 4х +5 и по графику выяснить её свойства: 1) найти значения х, при которых значения функции положительны и отрицательны; 2) промежутки возрастания (убывания); 3) при каком значении х функция принимает наибольшее (наименьшее) значение. Образовательный минимум по геометрии 8 класс
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 590; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.91.130 (0.007 с.) |





 -
-  .
. .
. см и 3см.
см и 3см.
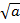 .
.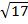 , -
, -  = │ a │.
= │ a │.
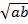 =
=  , a ≥ 0, в ≥ 0.
, a ≥ 0, в ≥ 0.
 2 = a, а ≥ 0.
2 = a, а ≥ 0.
 =
=  , a ≥ 0, в > 0
, a ≥ 0, в > 0
 ; 1,3(4)
; 1,3(4) ,
,  .
. 1)
1)  ; 2)
; 2) 





 ; 2) 5
; 2) 5  и 2
и 2  3) - 6,(39) и - 6,39.
3) - 6,(39) и - 6,39.
















 x1 =
x1 =  ,
x2 = -
,
x2 = -  , x2 = -
, x2 = -  .
.
 – дискриминант.
х1,2 =
– дискриминант.
х1,2 =  .
Замечание: если D< 0, то исходное уравнение не имеет решений, если D = 0, то - имеет одно решение, если D> 0, то имеет два решения.
Если х1, х2 – корни уравнения ах2 + bх + с = 0,
то при всех х справедливо равенство:
ах2 + bх + с = а(х – х1)(х – х2)
________________________________________
Теорема Виета
Если х1, х2 – корни приведенного квадратного уравнения х2 + pх + q = 0, то
х1 + х2 = - p, х1· х2 = q.
.
Замечание: если D< 0, то исходное уравнение не имеет решений, если D = 0, то - имеет одно решение, если D> 0, то имеет два решения.
Если х1, х2 – корни уравнения ах2 + bх + с = 0,
то при всех х справедливо равенство:
ах2 + bх + с = а(х – х1)(х – х2)
________________________________________
Теорема Виета
Если х1, х2 – корни приведенного квадратного уравнения х2 + pх + q = 0, то
х1 + х2 = - p, х1· х2 = q.
 2)
2)  3)
3)  ·
·  4)
4) 
 и
и  6) 2
6) 2  +
+  8) (
8) ( –
–  10)
10)  11)
11) 
 14) х2 = 13
15)
14) х2 = 13
15)  х2 = 0
х2 = 0









