
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выучить таблицу квадратов чисел с 11 до 25.Содержание книги
Поиск на нашем сайте
2.
3.
4.
5.
6.
7.
8.
4)
Задание 2. Тема: Свойства арифметического квадратного корня. (см. Алимов Алгебра 8.Гл.III, § 22-24). Сдать до 23.01.2016. 1. 2. 3. 4. 5. 6. Задание 3. Тема: Тождественные преобразования выражений, содержащих квадратные корни. (см. Алимов Алгебра 8.Гл.III, § 22-24). Сдать до 30.01.2016. 1.
2.
3.
4.
5.
6.
7.
8.
9.
10*.
4) 11*
Контрольная работа № 2
Задание 4. Теорема Виета. Уравнения, сводящиеся к квадратным. (см. Алимов 8.Гл.IV, § 29, § 30).Сдать до 6.02.2016 1.№450(2,4,6), 456(2,4,6), 455(2,4), 457(2,4,6,8), 458(4,6), 459*(2), 460*(4), 461*(4), 462*(2,4), 466*(1). 2. № 468(2), 469(4), 470(2), 471(2), 471*(4), 474*(2). Задание 5. Решение задач с помощью квадратных уравнений. (см. Алимов 8.Гл.IV, § 31).Сдать до 13.02.2016 1.№ 477, 478, 480, 481, 482, 483*, 484*, 485*, 486*, 491*. Задание 6. Решение простейших систем, содержащих уравнение второй степени. (см. Алимов 8.Гл.IV, § 31).Сдать до 20.02.2016 1.№ 492(4) – 497(4), 501*(2,4,6), 502*(2,4), 503*(2). 2. № 498, 499, 504*, 507*. Контрольная работа № 3
Геометрия Задание 1 Пропорциональные отрезки. Гл.VII, §1. п.56. Сдать до 24.01.2015 Письменно ответьте на следующие вопросы: А) Сформулируйте теорему Фалеса. Б) Что называют отношением двух отрезков? В) В каком случае говорят, что отрезки АВи СD пропорциональны отрезкам А1B1 и С1D1? Г) Сформулируйте теорему о пропорциональных отрезках. Д) Сформулируйте теорему о пересечении медиан треугольника. Е) Сформулируйте свойство биссектрисы треугольника.
1. Начертите произвольный отрезок и разделите его на семь равных частей. 2. Найдите отношение отрезков АВ и СО, если их длины соответственно равны 12 см и 18 см. Изменится ли это отношение, если длины данных отрезков выразить в дециметрах? в миллиметрах? 3. Среди отрезков АВ, СD, ЕР, МК, РS выберите четыре отрезка так, чтобы два из них были пропорциональны двум другим отрезкам, если АВ = 3 см, СD = 16 см, ЕF= 18 см, МК = 36 см, РS = 6 см. 4. На рисунке 123 ВD|| СЕ, АВ=16 см, ВС =6 см, АD =8 см. Найдите отрезок DЕ. B 6 C A 8 D E 5. Прямая, парaллельнаястороне ВС треугольника АВС, пересекает его сторону АВ в точке М, а сторону АС -в точке К. АМ= 9 см, ВМ= 6 см, КС =8 см.Найдите отрезок АК.
6. Расстояние от точки пересечения диагоналей прямоугольника до его большей стороны равно 7 см. Найдите длину меньшей стороны прямоугольника.
7. Медиана СD треугольника АВСравна 9 см. Найдите отрезки СО и ОD. где О— точка пересечения медиан треугольника АВС.
8. Отрезок АМ —биссектриса треугольника АВС, АВ= 48 см, АС= 32 см, ВМ -18 см. Найдите сторону ВС.
9. Сторона DЕ треугольника DЕF разделена на три равных отрезка, и через точки деления проведены прямые, параллельные сторон DF. Найдите отрезки этих прямых, если DF = 15см. 10. Средняя линия МК трапеции АВСD пересекает диагональ АС в точкеЕ, МЕ = 4 см, ЕК =6 см. Найдите основания трапеции.
11*. Основания трапеции равны 12 см и 22 см. Найдите отрезки, на которые диагонали трапеции делят её среднюю линию.
12*. Через точку О, отмеченную на стороне АС треугольника АВС, проведена прямая, которая параллельна стороне АВ и пересекает сторону ВС в точке Е, АО: ОС= 5:7, ВС = 36 см. Найдите отрезок ВЕ.
13*. Через точку D, отмеченную на стороне АС треугольника АВС, проведена прямая, которая параллельна стороне АВ и пересекает сторону ВС в точке Е, АD:DС= 5:7, ВС = 36 см. Найдите отрезок ВЕ.
14*. В треугольнике АВС (АВ - ВС) проведены медиана AМ и высота ВН. Найдите ВН, если АМ= 45 см, <САМ =30°. Задание 2 Подобные треугольники. Гл.VII, §1. п.57. Сдать до 31.01.2015 Письменно ответьте на следующие вопросы: a) Какие два треугольника называются подобными? b) Как найти коэффициент подобия двух подобных треугольников? c) Сформулируйте лемму о подобных треугольниках (задача 556 из учебника). 1. Найдите углы треугольника А]В]С1, если ΔАВС ~ΔА1В1С1 причём стороне АВ соответствует сторона А1В1 и стороне ВСсоответствует сторона В1С1<А = 25, <В= 70°.
2. Стороны МК и DЕ КТи EF — соответственные стороны подобных треугольников МКТи DEF, МК= 18 см, КТ= 16 см, МТ= 28 см, МК:DЕ=4:5. Найдите стороны треугольника DЕF.
3. В треугольнике АВС известно, что АВ = 6 см. Через точку М стороны АВ проведена прямая, которая параллельна стороне ВС и пересекает сторону АС в точке К. Найдитенеизвестные стороны треугольника АВС, если АМ = 4 см, МК= 8 см, АК = 9 см. 4. Продолжения боковых сторон АВ и СD трапеции АВСD пересекаются в точке М. Найдите меньшее основание трапеции, если большее основание АD равно 42 см, АВ= 9 см, ВМ = 54 см.
5. Точки М иК — середины сторон СD н АD квадрата АВСD соответственно. Пользуясь определением подобных треугольников, докажите, что ΔМDК ~ ΔВСD.
6. Стороны треугольника равны 15 см, 25 см и 35 см. Найдите стороны подобного ему треугольника, у которого: а) периметр равен 45 см; б) разность наибольшей и наименьшей сторон равна 16 см.
7. На рисунке изображеныпрямоугольный треугольник АВС (АВ= 90°) и вписанный в него квадрат ВМКN. Найдите СN если ВМ= 6 см, АВ= 10 см.
А М К
В NC
Задание 3 Первый признак подобия треугольников. Гл.VII, §2. п.59. Сдать до 6.02.2016 1. На рисунке DЕперпендикулярно АВ, ВС перпендикулярно АD. Укажите на этом рисунке все пары подобных треугольников. DC F BЕA 2. На стороне СD параллелограмма АВСD отмечена точка Е, прямые ВЕ и АD пересекаются в точке F, СЕ = 8см, DE = 4см, ВЕ = 10см, АD = 9см.Найдите длину отрезков EF и FD. BC E А F D 3. На рисунке DЕперпендикулярно АВ, ВС перпендикулярно АD. Укажите на этом рисунке все пары подобных треугольников. DC F BEA 4. На стороне СD параллелограмма АВСD отмечена точка Е, прямые ВЕ и АD пересекаются в точке F, СЕ = 8см, DE = 4см, ВЕ = 10см, АD = 9см.Найдите длину отрезков EF и FD. BC E А DF 5. Угол между боковой стороной и основанием одного равнобедренного треугольника равен углу между боковой стороной и основанием другого равнобедренного треугольника. Боковая сторона и основание первого треугольника равны 18 см и 10 см соответственно, а основание второго — 8 см. Найдите боковую сторону второго треугольника.
6. Стороны параллелограмма равны 20 см и 14 см, высота, проведённая к большей стороне, равна 7 см. Найдите высоту параллелограмма, проведённую к меньшей стороне.
7*. В трапеции АВСD (ВСǁАD) известно, что АD = 18 см, ВС = 14 см, АС = 24 см. Найдите отрезки, на которые диагональ АС делится точкой пересечения диагоналей.
8*. Докажите, что в подобных треугольниках высоты, проведённые из вершин соответственных углов, относятся как соответственные стороны.
9*. На стороне АС треугольника АВС отметили точку D такую, что <АВD = <С, AВ= 20 см. ВС =28 ем, АС= 40 см. Найдите неизвестные стороны треугольника AВD. Задание 4 Второй и третий признаки подобия треугольников. Гл.VII, §2. п.60, 61. Сдать до 13.02.2016 1. Отрезки АВи СDпересекаются в точкеО, АО =24 см, ВО= 16 см,СО= 15 см, ОD=10 см, <АСО= 72°.Найдите <ВDО. C В O
AD
2. На сторонах АС и ВСтреугольника АВСотметили соответственно точки МиКтак, что СМ =15 см,СК -12 см. Найдите МК,если АС =20 см, ВС= 25 см, АВ= 30 см. 3. Подобны ли два треугольника, если стороны одного относятся как 3:8: 9, а стороны другого равны 24 см, 9 см, 27 см?
4. В треугольниках DEFи МКN известно, что<Е = <К, а каждая из сторон DЕи ЕFв 2,5 раза больше сторон МК и КN соответственно. Найдите стороны DFи МN, если их разность равна 30 см. Задание 5 Метрические соотношения в прямоугольном треугольнике. Теорема Пифагора. Гл.VI, §3. п.54,55. Сдать до 20.03.2016 1.Катет прямоугольного треугольника равен 6 см, а его проекция на гипотенузу — 4 см. Найдите гипотенузу.
2. Высота прямоугольного треугольника, проведённая из вершины прямого угла, равна 48 см, а проекция одного из катетов на гипотенузу — 36см.
3. Найдите меньший катет прямоугольного треугольника и его высоту, проведённую к гипотенузе, если больший катет меньше гипотенузы па 10 см и больше своей проекции на гипотенузу на 8 см. 4. Запишите теорему Пифагора, если a и b катеты прямоугольного треугольника, а с – гипотенуза. Найдите неизвестную сторону прямоугольного треугольника, если: 1) а = 5см, b = 12см; 2) b = 3cм, с =
5. Сторона прямоугольника равна 7см, а диагональ – 25см. Найдите соседнюю к исходной сторону прямоугольника.
6. Высота равнобедренного треугольника, проведённая к основанию, равна 35см, а его основание – 24см. Чему равна боковая сторона треугольника?
7. Сторона ромба равна 26см, а одна из диагоналей - 48см. Найдите другую диагональ ромба. Гипотенуза прямоугольного треугольника равна 26см, а катеты относятся 5: 12. Найдите катеты этого треугольника. 8. В ΔАВС известно, что АВ = 17см, ВС = 9см, <С – тупой, высота АD = 8cм. Найдите сторону АС.
9. Найдите диагональ квадрата со стороной а. 10*. Найдите катеты прямоугольного равнобедренного треугольника, гипотенуза которого равна 10см.
11*. Высота равнобедренного треугольника, опущенная на боковую сторону, делит её на отрезки длиной 4см и 16см, считая от вершины угла при основании. Найдите основание равнобедренного треугольника. 12*. Стороны треугольника равны 36см, 29см и 25см. 13*. Найдите высоту треугольника, проведённую к большей стороне. Задание 6
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 483; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.126.241 (0.007 с.) |


















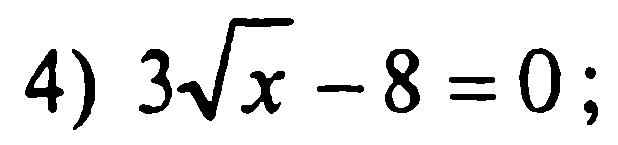 5)
5)  6*)
6*) 





 4*)
4*) 




 5)
5) 


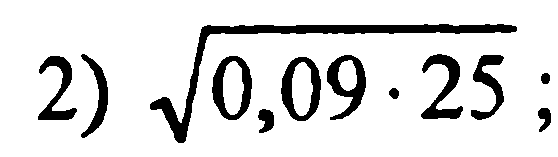




 4)
4)  ;
;




































 4*)
4*) 







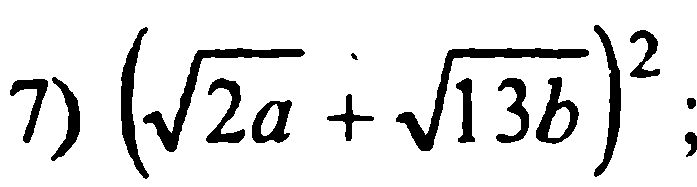

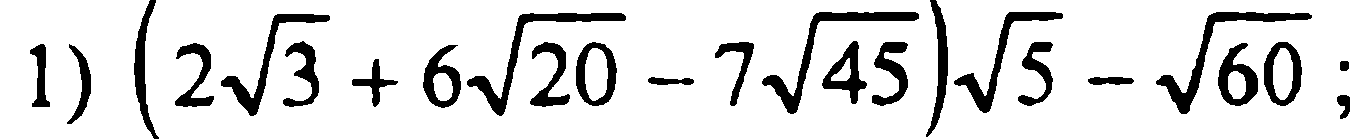














 3)
3) 
 5)
5) 








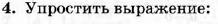











 см.
см.


