
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторное произведение в координатной формеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если (11.1) Выведем эту формулу:
= х1x2×( + y1x2×( + z1x2×( Векторы тогда при учете свойства 8.5 получим
+ y1x2×(- + z1x2×
Если дополнительно заменить каждую скобку соответствующим определителем второго порядка
то получим правило раскрытия определителя третьего порядка по первой строке (не вдаваясь в смысл Получили правило, по которому легко запомнить правило нахождения векторного произведения векторов в координатной форме: (11.2) Если векторы двумерные, то можно считать их третью координату нулевой,
8.5 Синус угла между векторами, заданными в координатной форме (12) sin ( 8.6 Двойное векторное произведение компланарный с (13) Двойное векторное произведение не обладает ни коммутативностью, ни дистрибутивностью. Пример 6 Базисом являются векторы В этом базисе заданы векторы Найти модуль векторного произведения векторов Решение: Составим векторное произведение векторов
= = 3×( = 3×( = 3×0 +14( Получили По определению | Ответ: |
Пример 7 Найти площадь треугольника АВС с вершинами в точках пространства А(2; 4; -1), В(3; 1; 1), С(0; 4; 2). Найти внутренний угол треугольника при вершине А и синус этого угла. Решение: 1) Найдем векторы Координаты вектора находятся вычитанием из координат конечной точки соответствующих координат начальной точки:
2) Площадь треугольника равна половине модуля векторного произведения образующих треугольник векторов, т.е. Векторное произведение векторов
=
Модуль векторного произведения следовательно
3) Угол при вершине А равен углу между отрезками АВ и АС, следовательно и между соответствующими векторами Угол между векторами можно найти по его косинусу, используя скалярное произведение векторов: cos( При этом синус угла можно найти из основного тригонометрического тождества В данном случае синус угла между векторами вычислим непосредственно, используя модуль векторного произведения (который уже найден): sin(
Найдём угол между векторами: ( Ответ: S=6,44, sin(ВАС)=0,883, (ВА^ВС)
|
|||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 528; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.160.135 (0.01 с.) |

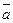 =(x1; y1; z1) и
=(x1; y1; z1) и 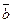 =(x2; y2; z2), то
=(x2; y2; z2), то .
.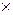
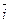 +y1×
+y1× 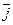 +z×
+z×  )
)  )+
)+ )+
)+ )+ z1y2×(
)+ z1y2×( ) + z1z2×(
) + z1z2×( .
. ,
, ;
; .
. =
=  ;
; или
или  - вектор,
- вектор, и
и  , он может быть найден по правилу
, он может быть найден по правилу .
. ,
,  .
. ,
, 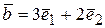 .
.
 – 4
– 4  )
) 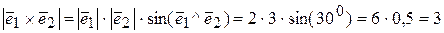 ,
, и
и  , образующие данный треугольник.
, образующие данный треугольник. .
. =
= ,
, =
=  ,
, ;
;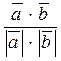 =
= 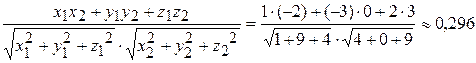 .
. .
. .
. 73 0.
73 0.


