
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Элементы векторной алгебры (12 часов, 6 лекций)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЛЕКЦИИ ПО ДИСЦИПЛИНЕ «Линейная алгебра» для направления 080100 «Экономика»
Рязань 2012 Тема 4. Элементы векторной алгебры (12 часов, 6 лекций) Лекция 1 Понятие геометрического вектора, его характеристики. Виды векторов В физике и других науках встречаются два типа величин: скалярные и векторные. Скалярные величины характеризуются численным значением в выбранной системе единиц. Это масса, температура, объем. Векторные величины характеризуются численным значением и направлением. Это сила, скорость, ускорение. Определение 1. Геометрический вектор - это направленный отрезок.
Определение 2. Модуль вектора, или длина вектора – это расстояние между на Определение 3. Два вектора называются равными, если они имеют одинаковую длину и одинаково направлены (параллельны и направлены в одну сторону).
Рис. 1 На рис. 1 векторы Определение 4. Два вектора называются коллинеарными, если они лежат на одной прямой или параллельны одной прямой ( Определение 5. Три вектора называются компланарными, если они лежат в одной плоскости или параллельны одной плоскости. Линейные операции над векторами в геометрической форме, Их свойства Сложение. а) правило параллелограмма: если векторы имеют общее начало, то сумма векторов – это вектор, являющийся диагональю параллелограмма, построенного на данных векторах.
Из рисунка видно, что
Рис. 1 б) правило треугольника: если векторы расположены последовательно, то есть конец первого является началом второго, то сумма векторов – это вектор, начало которого является началом первого, конец – это конец второго.
Рис. 2 Используя это правило, легко доказать, что
в) правило многоугольника: это обобщение правила треугольника, используется при последовательном расположении нескольких векторов, сумма нескольких последовательных векторов – это вектор, начало которого – это начало первого, а конец – это конец последнего.
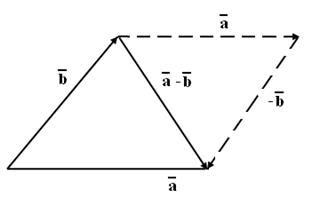
Определение 1. Вектор, начало и конец которого совпадают, называется нулевым, его длина равна нулю, направление любое. Определение 2. Если поменять начало и конец вектора местами, то получится вектор, противоположный данному. Вычитание.
Вычесть из одного вектора другой – это значит к данному вектору прибавить вектор, противоположный второму: Умножение вектора на число. Если данный вектор если если Если
Свойства операции 1. 3. 4. 5. 6. 7. Доказательство 4. Если если если 5.
Определение 3. Единичный вектор, направление которого совпадает с направлением вектора
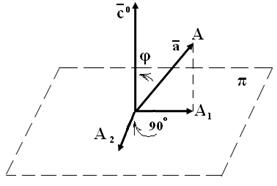
Лекция 2 Проекция вектора на вектор (ось), ее свойства. Направляющие косинусы вектора Рассмотрим вектор
Опустим из точек Определение. Проекцией вектора
Для рис. 1 имеем Найдем связь между проекцией вектора
но так как
Рассмотрим некоторые простейшие свойства проекции вектора 1) Из формулы (3.2) следует, что: если угол если угол если угол если угол 2) 3)
Координаты вектора (в базисе), разложение вектора по базису. Лекция 3 Понятие линейной зависимости и независимости системы векторов. Основные критерии (свойства) линейной зависимости, Доказательство. а) Пусть векторы
то есть вектор б) Пусть какой-то из векторов линейно выражается через остальные, например, вектор
тогда Теорема 2. Для того, чтобы два вектора были линейно зависимыми, необходимо и достаточно, чтобы они были коллинеарными. Доказательство. а) Пусть векторы б) Пусть векторы Теорема 3. Для того, чтобы три вектора были линейно зависимыми, необходимо и достаточно, чтобы они были компланарными. Доказательство. а)Пусть векторы б) Пусть векторы
что векторы линейно зависимы; если векторы
линейно зависимы.
Определение 2. Совокупность линейно независимых векторов таких, что любой вектор линейно выражается через эти векторы, называется базисом. Из приведенных теорем следует, что на плоскости базисом могут быть любые два неколлинеарных вектора, в пространстве базисом могут служить любые три некомпланарных вектора. Если векторы
тогда числа Лекция 4 Лекция 5 Доказательство.
3). Доказательство. а) Для б) для в) для 4).
Доказательство. Возьмем единичный вектор б) в)
Вектор получим Так как
5). 6). Для того, чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение было равно нулю. Доказательство. а) Пусть векторы
б) Пусть
7). 8). Векторные произведения базисных ортов можно представить в виде таблицы:
Пояснение: векторное произведение
Вычисление площадей. Если на векторах
Если на векторах
На плоскости векторное произведение не определено, а площадь параллелограмма вычисляется следующим образом:
Пример. Найти площадь параллелограмма, построенного на векторах Решение. Воспользуемся формулой. Для этого сначала вычислим векторное произведение данных векторов
Лекция 6 Свойства 1). Если в смешанном произведении поменять местами какие-то два множителя, то смешанное произведение изменит знак, то есть
2). Если в смешанном произведении сделать циклическую перестановку множителей, то произведение не изменится, то есть
3). Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю. Доказательство. 1) Пусть векторы а) один из векторов нулевой, например, плоскости двух других векторов(значит векторы компланарны), тогда
б) какие-то два вектора коллинеарны, например, кости, построенной на векторах есть векторы компланарны, тогда в) все векторы ненулевые и нет коллинеарных векторов, тогда
2) Пусть
ЛЕКЦИИ ПО ДИСЦИПЛИНЕ «Линейная алгебра» для направления 080100 «Экономика»
Рязань 2012 Тема 4. Элементы векторной алгебры (12 часов, 6 лекций) Лекция 1
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 669; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |



 ,
,  .
.
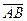 и
и  равные, векторы
равные, векторы  и
и 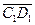 имеют разную длину, а векторы
имеют разную длину, а векторы  и
и  ,
, 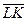 и
и  имеют разные направления.
имеют разные направления. ).
).

 .
.








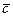


 .
. , получится следующий вектор
, получится следующий вектор  :
: , то
, то 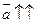
 ,
,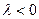 , то
, то  .
. , то длина вектора увеличится в
, то длина вектора увеличится в  раз, если
раз, если  , то длина уменьшается в
, то длина уменьшается в 
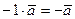 2.
2. 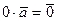





 , то
, то  ;
; , то
, то  ;
; и имеют разные знаки, то в обеих частях равенства будут нули.
и имеют разные знаки, то в обеих частях равенства будут нули.
 , называется ортом и обозначается
, называется ортом и обозначается  .
.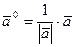 .
. и вектор (ось)
и вектор (ось)  (см. рис. 1). Осью называется прямая, на которой задано направление.
(см. рис. 1). Осью называется прямая, на которой задано направление.

 перпендикуляры на ось
перпендикуляры на ось  ,
,  (основания перпендикуляров) и соответствующий вектор
(основания перпендикуляров) и соответствующий вектор  . Параллельным переносом поместим вектор
. Параллельным переносом поместим вектор  , причем
, причем  угол между векторами
угол между векторами 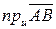 и равное длине вектора
и равное длине вектора  ) и
) и  , если вектор
, если вектор  ). Итак,
). Итак, (3.1)
(3.1) , так как
, так как  , так как
, так как 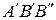 (он прямоугольный, так как
(он прямоугольный, так как 
 ). Тогда
). Тогда ,
, , то
, то  . Итак,
. Итак, на ось
на ось 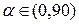 ), то
), то  , так как при
, так как при 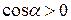 ;
; ), то
), то  , так как при
, так как при  ;
;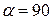 , то
, то  , так как при
, так как при 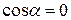 ;
; , то
, то  , так как при
, так как при  ;
;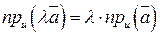 ;
; (
( – некоторый произвольный вектор).
– некоторый произвольный вектор). линейно зависимы, тогда в равенстве (2.2) хотя бы один из коэффициентов отличен от нуля, например,
линейно зависимы, тогда в равенстве (2.2) хотя бы один из коэффициентов отличен от нуля, например, 
 .В этом случае получаем
.В этом случае получаем ,
, линейно выражается через остальные.
линейно выражается через остальные. ,
, , коэффициент при
, коэффициент при  , а это и означает, что векторы коллинеарны.
, а это и означает, что векторы коллинеарны. , коэффициент при
, коэффициент при 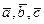 линейно зависимы, тогда один из них линейно выражается через остальные, например,
линейно зависимы, тогда один из них линейно выражается через остальные, например,  , отнесем эти векторы к одному началу, проведем через векторы
, отнесем эти векторы к одному началу, проведем через векторы  , тогда векторы
, тогда векторы  и
и 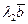 будут тоже принадлежать этой плоскости, следовательно, вектор
будут тоже принадлежать этой плоскости, следовательно, вектор  , значит вектор
, значит вектор 
 линейно выражается через эти векторы, то есть
линейно выражается через эти векторы, то есть ,
, являются координатами вектора
являются координатами вектора  .
.

 очевидно;
очевидно;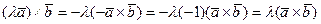 .
. .
.
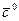 , перпендикулярный плоскости
, перпендикулярный плоскости  ,
,  . Спроектируем вектор
. Спроектируем вектор  , повернем его в плоскости
, повернем его в плоскости  по часовой стрелке на
по часовой стрелке на  : а)
: а)  ;
; (так как
(так как  ,
,  (так как
(так как 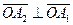 , а
, а  - правая тройка, следовательно,
- правая тройка, следовательно,  .
.
 . В
. В 
 . Спроектируем данный треугольник на плоскость
. Спроектируем данный треугольник на плоскость  , повернем его в плоскости
, повернем его в плоскости 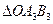 .
.  .
. , то
, то  .
. , тогда
, тогда  , следовательно,
, следовательно,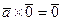 .
. или
или , тогда
, тогда 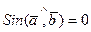 и
и 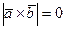 , нулевую длину имеет только нулевой вектор, то есть
, нулевую длину имеет только нулевой вектор, то есть  ;
; , тогда
, тогда  , следовательно,
, следовательно, .
.

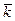


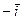
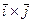 - это вектор, перпендикулярный векторам
- это вектор, перпендикулярный векторам  - правая тройка, отсюда следует, что
- правая тройка, отсюда следует, что 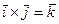 . Остальные произведения можно получить, используя свойства векторного произведения.
. Остальные произведения можно получить, используя свойства векторного произведения.
 .
. .
.
 .
. и
и  .
. , тогда
, тогда .
.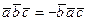 .
. .
.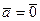 , у него любое направление, поэтому он лежит в
, у него любое направление, поэтому он лежит в ;
; , тогда вектор
, тогда вектор 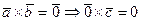 .
.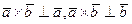 , то есть вектор
, то есть вектор  перпендикулярен плоскости векторов
перпендикулярен плоскости векторов  , тогда
, тогда  (свойство скалярного произведения).
(свойство скалярного произведения). , векторы ненулевые и нет коллинеарных векторов, отсюда следует, что
, векторы ненулевые и нет коллинеарных векторов, отсюда следует, что


