
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное произведение векторов: определение, свойства, вычислениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение 1. Углом между векторами
Определение 2. Скалярным произведением векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначения
Свойства скалярного произведения. 1). Коммутативность: 2). Доказательство. 3). Доказательство. 4). Доказательство. Из этого свойства следует, что
5). Для того, чтобы векторы были перпендикулярны Доказательство. а) Пусть векторы перпендикулярны и б) Пусть 6).
7.Для базисных ортов имеют место следующие соотношение
Скалярное произведение векторов в декартовой системе координат Пусть даны два вектора
воспользуемся свойством 7, получим формулу
Приложения скалярного произведения 1.Вычисление проекции
2.Вычисление косинуса угла между векторами
3.Условие перпендикулярности векторов
Пример. Даны векторы Решение. Воспользуемся формулой (2.19): вычисляем
Получаем Лекция 5 Векторное произведение векторов: определение, свойства, вычисление. Даны три вектора Определение 1. Тройка векторов
Если в тройке поменять местами какие-то два вектора, а третий оставить на своем месте, то тройка изменит свою “ориентацию”. Например, если Смысл декартовой тройки
Определение 2. Векторным произведением двух векторов 1. он перпендикулярен векторам 2. длина этого вектора равна площади параллелограмма, построенного на векторах 3. тройка Обозначения
Свойства векторного произведения 1) Антикоммутативность: Доказательство. Пусть
длины векторов
2). Если в векторном произведении изменить знак одного из множителей, то произведение тоже изменит знак: Доказательство.
3). Доказательство. а) Для б) для в) для 4).
Доказательство. Возьмем единичный вектор б) в)
Вектор получим Так как
5). 6). Для того, чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение было равно нулю. Доказательство. а) Пусть векторы
б) Пусть
7). 8). Векторные произведения базисных ортов можно представить в виде таблицы:
Пояснение: векторное произведение
Векторное произведение в декартовой системе координат Пусть
Приложения векторного произведения Вычисление площадей. Если на векторах
Если на векторах
На плоскости векторное произведение не определено, а площадь параллелограмма вычисляется следующим образом:
Пример. Найти площадь параллелограмма, построенного на векторах Решение. Воспользуемся формулой. Для этого сначала вычислим векторное произведение данных векторов
Лекция 6
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1276; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.34.105 (0.009 с.) |

 и
и  называется наименьший угол между этими векторами, отнесенными к общему началу.
называется наименьший угол между этими векторами, отнесенными к общему началу.

 (1)
(1) или
или  .
.


 , следует из определения.
, следует из определения. .
. .
.

 .
.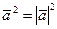
 .
. ,
,  .
.
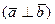 , необходимо и достаточно, чтобы их скалярное произведение было равно нулю
, необходимо и достаточно, чтобы их скалярное произведение было равно нулю  .
. , тогда
, тогда  ,следовательно,
,следовательно,  и
и  .
. - острый;
- острый; - тупой.
- тупой.
 , найдем их скалярное произведение
, найдем их скалярное произведение

 (2)
(2) (3)
(3) (4)
(4)
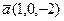 и
и 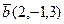 . Найти косинус угла между векторами.
. Найти косинус угла между векторами.
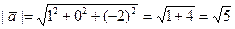 ,
,  ,
, .
.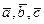 с общим началом и не лежащие в одной плоскости.
с общим началом и не лежащие в одной плоскости.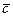 происходящим против (по) часовой стрелки.
происходящим против (по) часовой стрелки.
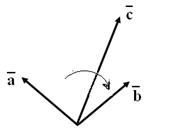
 - левая тройка. При циклической перестановке векторов в тройке “ориентация” тройки не меняется. Например, если
- левая тройка. При циклической перестановке векторов в тройке “ориентация” тройки не меняется. Например, если  - тоже правая тройка.
- тоже правая тройка. должен соответствовать выбранному правилу.
должен соответствовать выбранному правилу.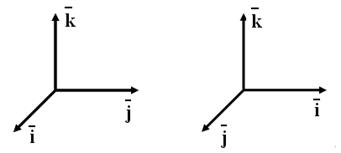
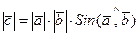 ;
; или
или  .
.
 .
.  , то есть
, то есть
 равны, но чтобы тройка векторов
равны, но чтобы тройка векторов  была правой, вектор
была правой, вектор  .
. .
.

 очевидно;
очевидно; : если длина одной из сторон параллелограмма изменяется в
: если длина одной из сторон параллелограмма изменяется в  раз, то площадь параллелограмма тоже изменится в
раз, то площадь параллелограмма тоже изменится в 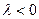 :
: 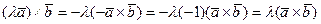 .
. .
.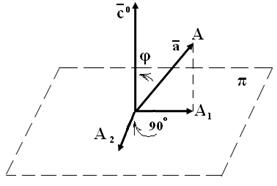
 , перпендикулярный плоскости
, перпендикулярный плоскости  ,
,  . Спроектируем вектор
. Спроектируем вектор  , повернем его в плоскости
, повернем его в плоскости  по часовой стрелке на
по часовой стрелке на  : а)
: а)  ;
; (так как
(так как  ,
,  (так как
(так как 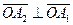 , а
, а  - правая тройка, следовательно,
- правая тройка, следовательно,  .
.
 . В
. В 
 . Спроектируем данный треугольник на плоскость
. Спроектируем данный треугольник на плоскость  , повернем его в плоскости
, повернем его в плоскости 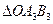 .
.  .
. , то
, то  .
. , тогда
, тогда  , следовательно,
, следовательно,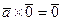 .
. или
или , тогда
, тогда 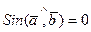 и
и 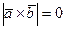 , нулевую длину имеет только нулевой вектор, то есть
, нулевую длину имеет только нулевой вектор, то есть  ;
; , тогда
, тогда  , следовательно,
, следовательно, .
.

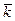


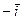
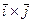 - это вектор, перпендикулярный векторам
- это вектор, перпендикулярный векторам 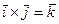 . Остальные произведения можно получить, используя свойства векторного произведения.
. Остальные произведения можно получить, используя свойства векторного произведения.



 .
. .
. .
.
 .
. и
и  .
. , тогда
, тогда .
.


