Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное произведение Дубль ДваСодержание книги
Поиск на нашем сайте
Скалярное произведение
Скалярное произведение векторов
где Из определения скалярного произведения следует, что Скалярный квадрат вектора: Свойства скалярного произведения:
Если
Векторное произведение векторов 1) 2) 3) тройка Свойства векторного произведения:
TRIPPLE VECT ОЙКИ МАТЬ ИХ 11.1. Правые и левые тройки векторов и системы координат. Определение. Три вектора называются упорядоченной тройкой (или просто трой- кой), если указано, какой из этих векторов является первым, какой - вторым и какой - третьим. При записи тройки векторов мы всегда будем располагать эти векторы в порядке их следования. Так, запись bac означает, что первым элементом тройки является вектор b, вторым - вектор a и третьим - вектор c. Определение. Тройка не компланарных векторов abc называется правой (левой), если выполнено одно из следующих трех условий: 1. если, будучи приведены к общему началу, эти векторы распо- лагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки; 2. если после приведения к общему началу вектор c располагает- ся по ту сторону от плоскости, определяемой векторами a и b, откуда кратчайший поворот от a к b кажется совершаю- щимся против часовой стрелки (по часовой стрелке); 3. если, находясь внутри телесного угла, образованного приведен- ными к общему началу векторами a, b, c, мы видим поворот от a к b и от него к c совершающимся против часовой стрелки (по часовой стрелке). Легко проверить, что условия 1, 2 и 3 эквивалентны между собой. Заметим также, что понятие правой и левой тройки теряет смысл для компланарных векторов. Если две тройки векторов либо обе являются правыми, либо обе являются левыми, то говорят, что эти тройки одной ориентации. В противном случае
говорят, что рассматриваемые две тройки противоположной ориентации. Всего из трех векторов a, b и можно составить следующие шесть троек: abc, bca, cab, bac, acb, cba. Тройки abc, bca, cab - правые, а bac, acb, cba - левые.
Векторное произведение Векторным произведением вектора
Векторное произведение обозначается квадратными скобками:
Свойства векторного произведения:
27. Смешанным произведением трех векторов Геометрический смысл смешанного произведения: если тройка векторов Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах
Объем пирамиды, построенной на этой тройке векторов равен
1° 2° 3° Три вектора компланарны тогда и только тогда, когда 4° Тройка векторов является правой тогда и только тогда, когда 5° 6° 7° 8° 9° 10° Тождество Якоби: Если векторы
|
||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.250 (0.009 с.) |

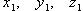 и
и 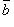 :
: 
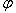 - угол между векторами
- угол между векторами  и
и 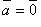 либо
либо  , то
, то 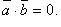
 где, например,
где, например, 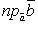 есть величина проекции вектора
есть величина проекции вектора 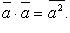

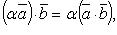



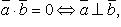


 то
то 
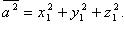
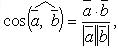
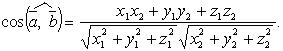
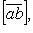
 или
или 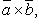 для когорого:
для когорого: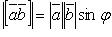 (
(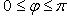 );
);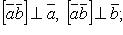

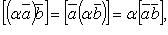
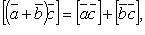
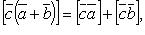
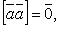
 если
если  , то
, то 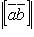 равен площади параллелограмма, построенного на приведенных к общему началу векторах
равен площади параллелограмма, построенного на приведенных к общему началу векторах  на вектор
на вектор  называется третий вектор
называется третий вектор 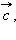 который обладает следующими свойствами:
который обладает следующими свойствами: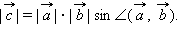
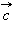 перпендикулярен к плоскости, в которой лежат вектора
перпендикулярен к плоскости, в которой лежат вектора 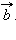
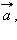
 и
и 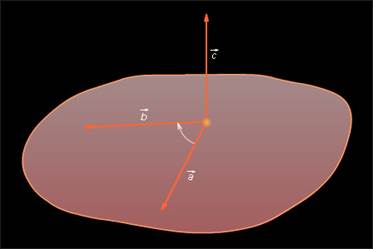
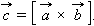
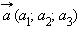 и
и 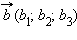 следующие
следующие 
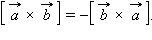
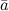 ,
, 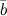 ,
, 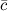 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 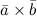 на вектор
на вектор 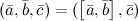
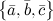 правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах:
правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: 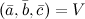 . В случае левой тройки
. В случае левой тройки 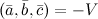 . Если
. Если 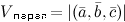

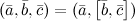
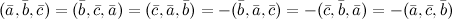
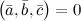
 . Если же
. Если же  , то векторы
, то векторы 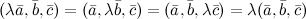
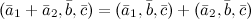


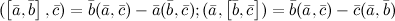

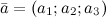 ,
,  и
и 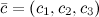 заданы своими координатами, то их смешанное произведение вычисляется по формуле
заданы своими координатами, то их смешанное произведение вычисляется по формуле