Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрицы, сложения, вычитание, умножениеСодержание книги
Поиск на нашем сайте
1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу). Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак: 2) Действие второе. Умножение матрицы на число.
Единственное, что желательно сделать в этом примере – это внести минус в матрицу: А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить. 3) Действие третье. Транспонирование матрицы. Потом переписываем вторую строку во второй столбец: 4) Действие четвертое. Сумма (разность) матриц. НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Действие пятое. Умножение матриц Чтобы матрицу
Умножить матрицу Формула:
Обратите внимание, что Таким образом, при умножении переставлять матрицы нельзя!
Определители, свойства, алгебраические дополнения, вычисления Обозначения: Если дана матрица
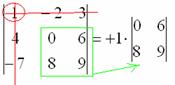
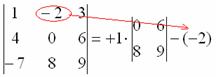
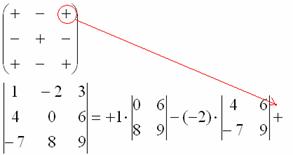
Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ. Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький. Коль скоро выбран способ разложения определителя по первой строке, очевидно, что всё вращается вокруг неё: 1) Из матрицы знаков выписываем соответствующий знак: 2) Затем записываем сам элемент: 3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент: Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы). Переходим ко второму элементу строки. 4) Из матрицы знаков выписываем соответствующий знак:
5) Затем записываем второй элемент: 6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент: Ну и третий элемент первой строки. Никакой оригинальности:
7) Из матрицы знаков выписываем соответствующий знак: 8) Записываем третий элемент: 9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:
1. Определитель выгоднее раскрывать по ТОЙ строке (столбцу), где: 1) нулей побольше; Из чего следует важный факт: строки и столбцы определителя равноправны. 2. Если две строки (или два столбца) определителя поменять местами, То есть, любая парная перестановка строк (столбцов) влечёт изменение знака определителя на противоположный. 3. Из строки (столбца) определителя можно вынести общий множитель !!! Внимание! В правиле речь идёт об ОДНОЙ строке или об ОДНОМ столбце определителя. Пожалуйста, не путайте с матрицами, в матрице множитель выносится/вносится у ВСЕХ чисел сразу. Справедливо и обратное правило – множитель можно не только вынести, но и внести, причём, в ЛЮБУЮ строку или в ЛЮБОЙ столбец определителя. 4. Если две строки (столбца) определителя пропорциональны Определитель с нулевой строкой (столбцом) равен нулю Какие свойства определителей полезно знать? 1) Величина определителя не меняется при транспонировании. Свойство запоминаем. 2) Любая парная перестановка строк (столбцов) меняет знак определителя на противоположный. Свойство тоже запоминаем и стараемся не использовать во избежание путаницы. 3) Из строки (столбца) определителя можно вынести множитель (и внести его обратно). Используем там, где это выгодно. Если строки (столбцы) определителя пропорциональны, то он равен нулю. Определитель с нулевой строкой (столбцом) равен нулю.
Система линейных уравнений теорема Крамера Запись систем линейных уравнений в матричной форме
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 411; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.82.70 (0.009 с.) |






 можно было умножить на матрицу
можно было умножить на матрицу  нужно, чтобы число столбцов матрицы
нужно, чтобы число столбцов матрицы
 – попытайтесь сразу уловить закономерность.
– попытайтесь сразу уловить закономерность.
 на матрицу
на матрицу 


 ! Это почти всегда так!
! Это почти всегда так!
 , то ее определитель обозначают
, то ее определитель обозначают 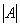 . Также очень часто определитель обозначают латинской буквой
. Также очень часто определитель обозначают латинской буквой  или греческой
или греческой  .
.