
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Угол между двумя плоскостями. Параллельность и перпендикулярность двух плоскостей. Взаимное расположение трех плоскостейСодержание книги
Поиск на нашем сайте
Зададим две плоскости
Мы знаем, что векторы
поэтому
Достаточно считать, что Отметим, что две пересекающиеся плоскости на самом деле образуют два двугранных угла Две плоскости (14) перпендикулярны тогда и только тогда, когда
Две плоскости (14) параллельны тогда и только тогда, когда (перпендикулярные к ним) векторы
Если дополнительно к этому выполняются расширенные условия пропорциональности
то это говорит о том, что плоскости (14) совпадают, т.е. оба уравнения (14) определяют одну и ту же плоскость. Хотя на нуль делить нельзя, но удобно писать символические пропорции (17) или (18) с нулями. Но тогда, если, например, Пример 1. Уравнения
определяют пару параллельных плоскостей, а уравнения
- пару совпадающих плоскостей. Пусть относительно ПДСК заданы три плоскости π1, π2, π3 своими общими уравнениями: A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0, A3x+B3y+C3z+D3=0.
30. Прямая как линия пересечения двух плоскостей Пусть относительно ПДСК заданы две плоскости своими общими уравнениями, пересекающихся по некоторой прямой: α: A1x+B1y+C1z+D1=0. β: A2x+B2y+C2z+D2=0. Запишем канонические уравнения прямой, полученные в результате пересечения плоскостей α и β. Пусть x0, y0, z0 - какое-либо решение {A1x+B1y+C1z+D1=0. {A2x+B2y+C2z+D2=0. Точка M0(x0, y0, z0) принадлежит прямой пересечения плоскостей α и β. Покажем, что в качестве направляющего вектора прямой можно взять вектор a с координатами {B1 C1 C1 A1 A1 B1} {B2 C2,C2 A2,A2 B2}. В самом деле, в силу необходимого и достаточного условия компланарности вектора и плоскости имеем N1={A1, B1, C1}, N2={A2, B2, C2}.
Угол между двумя прямыми Угол φ между двумя прямыми, заданными общими уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, вычисляется по формуле:
4. Условия параллельности двух прямых: а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k 1 = k 2. (8) б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
5. Условия перпендикулярности двух прямых: а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
Пересекающимися, скрещивающиеся, паралельные
32. прямая м плоскость. Угол между прямой и плоскость. Паралельность и перпендикулярность прямой и плоскости. Вазимное расположение прямой и плоскости
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.231.116 (0.006 с.) |

 (14)
(14) и
и  перпендикулярны соответственно данным плоскостям, поэтому угол
перпендикулярны соответственно данным плоскостям, поэтому угол  между
между 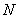 и
и  равен углу (двугранному) между данными плоскостями. Но скалярное произведение
равен углу (двугранному) между данными плоскостями. Но скалярное произведение ,
, . (15)
. (15) .
. и
и  Их сумма равна
Их сумма равна  , а их косинусы равны по абсолютной величине, но отличаются знаками (
, а их косинусы равны по абсолютной величине, но отличаются знаками ( ). Если заменить в первом уравнении (14) числа
). Если заменить в первом уравнении (14) числа  ,
, 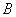 ,
,  соответственно на числа
соответственно на числа 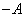 ,
, 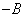 ,
,  , то полученное уравнение будет определять ту же плоскость, но угол
, то полученное уравнение будет определять ту же плоскость, но угол  .
. , т. е.
, т. е. . (16)
. (16) . (17)
. (17)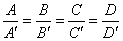 , (18)
, (18) , то надо и
, то надо и  . Или если
. Или если  , то
, то  .
.

 Введем следующие обозначения: Определим через n1, n2, n3 нормальные векторы π1, π2, π3, то есть n1={A1, B1, C1}, n2={A2, B2, C2}, n3={A3, B3, C3}. Сформулируем следующие утверждения, выражающие необходимые и достаточные условия взаимного расположения плоскостей π1, π2, π3. Если δ≠0, то плоскости π1, π2, π3 имеют единственную точку пересечения. A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0, A3x+B3y+C3z+D3=0. Если rang m=2, rang M=3 и среди векторов n1, n2, n3 нет коллинеарных, то все три плоскости попарно пересекаются, причем прямые пересечения попарно различны. Если rang m=2, rang M=3 и среди векторов n1, n2, n3 есть два неколлинеарных, то две плоскости параллельны друг другу, а третья их пересекает. Если rang m=2, rang M=2 и среди векторов n1, n2, n3 нет коллинеарных, то все три плоскости пересекаются по одной прямой. Если rang m=2, rang M=2 и среди векторов n1, n2, n3 есть два коллинеарных, то две плоскости совпадают, а третья плоскость их пересекает по одной прямой. Если rang M=1, то все три плоскости совпадают. Если rang m=1 и коэффициенты любых двух уравнений плоскостей π1, π2, π3 непропорциональны, то все три плоскости параллельны друг другу. Если rang m=1 и коэффициенты любых двух уравнений плоскостей π1, π2, π3 пропорциональны, то две плоскости совпадают, а третья им параллельна.
Введем следующие обозначения: Определим через n1, n2, n3 нормальные векторы π1, π2, π3, то есть n1={A1, B1, C1}, n2={A2, B2, C2}, n3={A3, B3, C3}. Сформулируем следующие утверждения, выражающие необходимые и достаточные условия взаимного расположения плоскостей π1, π2, π3. Если δ≠0, то плоскости π1, π2, π3 имеют единственную точку пересечения. A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0, A3x+B3y+C3z+D3=0. Если rang m=2, rang M=3 и среди векторов n1, n2, n3 нет коллинеарных, то все три плоскости попарно пересекаются, причем прямые пересечения попарно различны. Если rang m=2, rang M=3 и среди векторов n1, n2, n3 есть два неколлинеарных, то две плоскости параллельны друг другу, а третья их пересекает. Если rang m=2, rang M=2 и среди векторов n1, n2, n3 нет коллинеарных, то все три плоскости пересекаются по одной прямой. Если rang m=2, rang M=2 и среди векторов n1, n2, n3 есть два коллинеарных, то две плоскости совпадают, а третья плоскость их пересекает по одной прямой. Если rang M=1, то все три плоскости совпадают. Если rang m=1 и коэффициенты любых двух уравнений плоскостей π1, π2, π3 непропорциональны, то все три плоскости параллельны друг другу. Если rang m=1 и коэффициенты любых двух уравнений плоскостей π1, π2, π3 пропорциональны, то две плоскости совпадают, а третья им параллельна.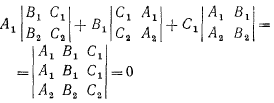 Так как определитель содержит две одинаковые строки, то направляющий вектор прямой, полученный в результате пересечения плоскостей α и β, компланарен плоскости α, а значит, и сама прямая компланарна плоскости α. Аналогично проверяем компланарность направляющего вектора прямой и плоскости β. Таким образом, вектор а можно выбрать в качестве направляющего вектора прямой, полученной в результате пересечения плоскостей α и β. Каноническое уравнение прямой имеет вид:
Так как определитель содержит две одинаковые строки, то направляющий вектор прямой, полученный в результате пересечения плоскостей α и β, компланарен плоскости α, а значит, и сама прямая компланарна плоскости α. Аналогично проверяем компланарность направляющего вектора прямой и плоскости β. Таким образом, вектор а можно выбрать в качестве направляющего вектора прямой, полученной в результате пересечения плоскостей α и β. Каноническое уравнение прямой имеет вид: 


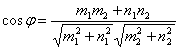



 (9)
(9)


 (10)
(10)


