
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Базис в пространстве и на плоскости. Разложение по базисуСодержание книги
Поиск на нашем сайте
где Проанализируем линейную зависимость векторов на плоскости и в пространстве. Т.1: Два вектора являются коллинеарными в том и только в том случае, когда они линейно зависимы ■ □ Поскольку согласно условию векторы Следствие: Два неколлинеарных вектора линейно независимы.
Рис. 2.5 Т.2: Пусть векторы □ Поместим начала векторов Из Т.2 и её доказательства имеем следствие. Следствие. Три вектора компланарны тогда и только тогда, когда они линейно зависимы. Т.3: Допустим, что □ Помещаем начала векторов Следствие: Любые четыре вектора в пространстве линейно зависимы.
Рис. 2.6 О: Базисом на плоскости и пространстве именуется максимальная линейно независимая на плоскости или в пространстве система векторов (при добавлении к системе ещё одного вектора система становится линейно зависимой). Следовательно, базисом на плоскости будут всякие два неколлинеарных вектора, которые взяты в определённом порядке, а базисом в пространстве будут всякие три некомпланарных вектора, которые взяты в определённом порядке. Пусть Запись через координаты линейных операций над векторами: а) сложение и вычитание:
б) Умножение на число
Формулы вытекают из свойства линейных операций. Задача. Найти координаты ◄ Стоит отметить, что если векторы
37. прямые второго порядка эллипс гипербола парабола Общий вид линии второго порядка: К кривым второго порядка относятся: окружность, эллипс, гипербола, парабола. 1. Окружность где Если центр окружности совпадает с началом координат, то уравнение имеет вид
Рис. 2 Эллипс Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (бóльшая, чем расстояние между фокусами). Каноническое (простейшее) уравнение эллипса с центром в начале координат и с фокусами в точках где
Рис. 3
Если центр эллипса находится в точке Гипербола Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами. Уравнение гиперболы с центром в начале координат и с фокусами в точках где Коэффициенты Прямые
Рис. 4 Если центр гиперболы находится в точке Парабола Параболой называется множество точек плоскости, равноудаленных от точки, называемой фокусом и прямой, называемой директрисой. Уравнение параболы с вершиной в начале координат имеет вид: где
Если вершина параболы находится в точке
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.255.58 (0.006 с.) |

 (2.1)
(2.1) представляют собой произвольные действительные числа. Векторы
представляют собой произвольные действительные числа. Векторы  являются линейно зависимыми, при условии
являются линейно зависимыми, при условии  , что линейная комбинация (2.1) равняется нулю, а в противном случае они будут линейно независимыми.
, что линейная комбинация (2.1) равняется нулю, а в противном случае они будут линейно независимыми. — коллинеарны
— коллинеарны  )
)
 и
и 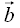 являются неколлинеарными, в этом случае любой компланарный с ними вектор
являются неколлинеарными, в этом случае любой компланарный с ними вектор  представляется исключительным образом как их линейная комбинация ■
представляется исключительным образом как их линейная комбинация ■ . Допустим, что найдутся
. Допустим, что найдутся  , для которых также
, для которых также  . Согласно свойствам линейных операций получаем
. Согласно свойствам линейных операций получаем 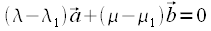 , и отсюда в силу следствия Т.1
, и отсюда в силу следствия Т.1  ,
, 
 некомпланарны, тогда всякий вектор
некомпланарны, тогда всякий вектор 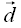 в пространстве единственным образом представляется как их линейная комбинация ■
в пространстве единственным образом представляется как их линейная комбинация ■ (рис. 2.6). В этом случае согласно Т.2 вектор
(рис. 2.6). В этом случае согласно Т.2 вектор  и
и 

 .
. — базис
— базис
 :
: .
. в базисе
в базисе  .
. в этом же базисе.
в этом же базисе. ►
► и наоборот.
и наоборот. . (1)
. (1) (2)
(2) - радиус окружности,
- радиус окружности,  и
и  - координаты центра окружности.
- координаты центра окружности. (3)
(3)
 и
и 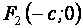 :
: (4)
(4) эллипса связаны соотношением
эллипса связаны соотношением 

 , то уравнение эллипса имеет вид:
, то уравнение эллипса имеет вид: (5)
(5) (6)
(6) и
и  гиперболы связаны соотношением
гиперболы связаны соотношением  .
. - асимптоты гиперболы.
- асимптоты гиперболы.
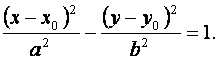 (7)
(7) , (8)
, (8)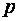 - расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты
- расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты  .
.




