
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как определить коллинеарность векторов пространства?Содержание книги
Поиск на нашем сайте
Правило очень похоже. Для того чтобы два вектора пространства 16. базис. Разложение по базису. Координатный столбец вектора. Теорема о базисе. Теорема о единственности разложения по базису. Пример!!! Разложение вектора по базису. Определение. Пусть
то говорят, что вектор Теорема. (О разложении вектора по базису.) Любой вектор векторного пространства можно разложить по его базису и притом единственным способом. Доказательство. 1) Пусть L произвольная прямая (или ось) и Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора
Так как 2) Пусть теперь Р произвольная плоскость и Теперь, по уже доказанному в первой части этого доказательства, существуют такие числа
рис.3. Теперь докажем единственность разложения по базису. Допустим противное. Пусть имеется два разложения вектора
3) Пусть Отложим все три базисных вектора
рис.4. По правилу сложения векторов получаем равенство:
По построению
и возможность разложения по базису доказана. Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора
Заметим, что по условию векторы Возможны два случая: а) Пусть
Из равенства (4) следует, что вектор б) Остается случай
Так как Теорема доказана. 18. евклидово пространство скалярное произведение. Норма. Длина. Угол. Неравество каши куниковского. Пример!!! Определение Действительное линейное пространство E называется евклидовым, если каждой паре векторов I. II. III. IV. Число
Длина вектора Свойства: 1) 2) 3) 4) Углом между векторами
Ортогональные векторы
Векторы Нормированные векторы Вектор Если Система векторов
называется ортонормированной. Во всяком пространстве
...............
Пронормировав каждый вектор
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.110.198 (0.012 с.) |

 были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны
были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны 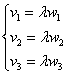 .
. – произвольный вектор,
– произвольный вектор,  – произвольная система векторов. Если выполняется равенство
– произвольная система векторов. Если выполняется равенство , (1)
, (1) называются в этом случае координатами вектора
называются в этом случае координатами вектора  –базис
–базис  . Возьмем произвольный вектор
. Возьмем произвольный вектор  . Так как оба вектора
. Так как оба вектора  и
и  коллинеарные одной и той же прямой L, то
коллинеарные одной и той же прямой L, то  . Воспользуемся теоремой о коллинеарности двух векторов. Так как
. Воспользуемся теоремой о коллинеарности двух векторов. Так как  , то найдется (существует) такое число
, то найдется (существует) такое число  , что
, что  и тем самым мы получили разложение вектора
и тем самым мы получили разложение вектора  , где
, где  . Тогда
. Тогда  и используя закон дистрибутивности, получаем:
и используя закон дистрибутивности, получаем: .
. , ч.т.д.
, ч.т.д. – базис
– базис  . Пусть
. Пусть  произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведемпрямую
произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведемпрямую  , на которой лежит вектор
, на которой лежит вектор  , прямую
, прямую  , на которой лежит вектор
, на которой лежит вектор  . Через конец вектора
. Через конец вектора  , и
, и  ,
,  ,
,  – базис
– базис  , что
, что и
и  . Отсюда получаем:
. Отсюда получаем: и возможность разложения по базису доказана.
и возможность разложения по базису доказана.
 и
и  . Получаем равенство
. Получаем равенство , откуда следует
, откуда следует  . Если
. Если 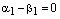 , то
, то  , а т.к.
, а т.к.  , то
, то  и коэффициенты разложения равны:
и коэффициенты разложения равны:  ,
,  . Пусть теперь
. Пусть теперь  . Тогда
. Тогда 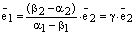 , где
, где  . По теореме о коллинеарностидвух векторов отсюда следует, что
. По теореме о коллинеарностидвух векторов отсюда следует, что  . Получили противоречие условию теоремы. Следовательно,
. Получили противоречие условию теоремы. Следовательно,  – базис
– базис  и пусть
и пусть  произвольный вектор. Проведем следующие построения.
произвольный вектор. Проведем следующие построения. и вектор
и вектор  , плоскость
, плоскость  и плоскость
и плоскость  ; далее через конец вектора
; далее через конец вектора 
 . (1)
. (1) . Отсюда, по теореме о коллинеарности двухвекторов, следует, что существует число
. Отсюда, по теореме о коллинеарности двухвекторов, следует, что существует число 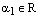 , такое что
, такое что  . Аналогично,
. Аналогично,  , где
, где  . Теперь, подставляя эти равенства в (1), получаем:
. Теперь, подставляя эти равенства в (1), получаем: (2)
(2) . Тогда
. Тогда . (3)
. (3) . (4)
. (4) , т.е. вектор
, т.е. вектор  . Тогда из равенства (3) получаем
. Тогда из равенства (3) получаем 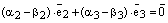 или
или . (5)
. (5) , ч.т.д.
, ч.т.д. сопоставляется число
сопоставляется число 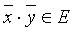 так, что
так, что  и
и  выполняются аксиомы:
выполняются аксиомы:



 называют скалярным произведением векторов
называют скалярным произведением векторов  и
и  ,
,  - скалярным квадратом вектора
- скалярным квадратом вектора 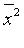 ). Введенная операция называется скалярным умножением векторов
). Введенная операция называется скалярным умножением векторов  - число
- число 


 (неравенство Коши-Буняковского);
(неравенство Коши-Буняковского); (неравенство треугольника).
(неравенство треугольника).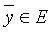 называют угол
называют угол  , для которого
, для которого
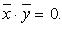

 то соответствующими этому вектору нормированными векторами будут
то соответствующими этому вектору нормированными векторами будут 
 для которой
для которой
 существует ортонормированный базис. Из произвольного базиса
существует ортонормированный базис. Из произвольного базиса  пространства
пространства 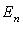 ортогональный базис может быть построен с помощью процесса ортогонализации:
ортогональный базис может быть построен с помощью процесса ортогонализации: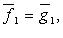
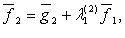 где
где 
 где
где 
 где
где 
 получим ортонормированный базис. В ортонормированном базисе (
получим ортонормированный базис. В ортонормированном базисе ( ) для векторов
) для векторов 
 имеем:
имеем:



