
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расстояние между скрещивающимися прямыми – определение.Содержание книги
Поиск на нашем сайте
Прежде чем дать определение расстояния между скрещивающимися прямыми, напомним определение скрещивающихся прямых и докажем теорему, связанную со скрещивающимися прямыми. В разделе взаимное расположение прямых в пространстве мы упоминали, что две прямые называются скрещивающимися, если они не лежат в одной плоскости. Теорема. Через каждую из скрещивающихся прямых проходит единственная плоскость, которой параллельна другая прямая. Доказательство. Пусть даны скрещивающиеся прямые a и b. Докажем, что через прямую b проходит единственная плоскость, параллельная прямой a (абсолютно аналогично можно будет доказать, что через прямую a проходит плоскость, параллельная прямой b, притом только одна). Это будет служить доказательством теоремы. Отметим на прямой b некоторую точку Q. В статье параллельные прямые, параллельность прямых была доказана теорема, гласящая, что через произвольную точку пространстве проходит единственная прямая, параллельная заданной прямой. Следовательно, через точку Q можно провести единственную прямую, параллельную прямой a. Обозначим ее a1. В разделе способы задания плоскости мы упоминали, что через две пересекающиеся прямые проходит единственная плоскость (что следует из аксиомы о плоскости, проходящей через три различные точки, не лежащие на одной прямой). Следовательно, через пересекающиеся прямые b и a1 проходит единственная плоскость. Обозначим ее Признак параллельности прямой и плоскости позволяет утверждать, что прямая a параллельна плоскости Единственность плоскости
Теперь можно переходить непосредственно к определению расстояния между скрещивающимися прямыми. Определение расстояния между скрещивающимися прямыми дается через расстояние между прямой и параллельной ей плоскостью. Определение. Расстояние между скрещивающимися прямыми – это расстояние между одной из скрещивающихся прямых и параллельной ей плоскостью, проходящей через другую прямую. В свою очередь расстояние между прямой и параллельной ей плоскостью есть расстояние от некоторой точки прямой до плоскости. Тогда справедлива следующая формулировка определения расстояния между скрещивающимися прямыми.
Определение. Расстояние между скрещивающимися прямыми – это расстояние от некоторой точки одной из скрещивающихся прямых до плоскости, проходящей через другую прямую параллельно первой прямой. Рассмотрим скрещивающиеся прямые a и b. Отметим на прямой a некоторую точку М1, через прямую b проведем плоскость
К началу страницы Нахождение расстояния между скрещивающимися прямыми – теория, примеры, решения. При нахождении расстояния между скрещивающимися прямыми основная сложность часто заключается в том, чтобы увидеть или построить отрезок, длина которого равна искомому расстоянию. Если такой отрезок построен, то в зависимости от условий задачи его длина может быть найдена с помощью теоремы Пифагора, признаков равенства или подобия треугольников и т.п. Так мы и поступаем при нахождении расстояния между скрещивающимися прямыми на уроках геометрии в 10-11 классах. Если же в трехмерном пространстве введена прямоугольная система координат Oxyz и в ней заданы скрещивающиеся прямые a и b, то справиться с задачей вычисления расстояния между заданными скрещивающимися прямыми позволяет метод координат. Давайте его подробно разберем. Пусть Теперь подробно. Задача сводится к получению координат точки М1, лежащей на прямой a, и к нахождению нормального уравнения плоскости С определением координат точки М1 сложностей не возникает, если хорошо знать основныевиды уравнений прямой в пространстве. А вот на получении уравнения плоскости
Если мы определим координаты В качестве точки М2 можно взять любую точку, лежащую на прямой b, так как плоскость Осталось получить координаты нормального вектора плоскости Плоскость Итак, мы имеем общее уравнение плоскости Остается только привести общее уравнение плоскости к нормальному виду Таким образом, чтобы найти расстояние между скрещивающимися прямыми a и b нужно: · определить координаты · получить координаты · найти координаты · записать общее уравнение плоскости · привести полученное уравнение плоскости · вычислить расстояние Разберем решение примера. Пример. В трехмерном пространстве в прямоугольной системе координат Oxyz заданы две скрещивающиеся прямые a и b. Прямую a определяют параметрические уравнения прямой в пространстве вида Решение. Очевидно, прямая a проходит через точку Вычислим векторное произведение векторов Таким образом, нормальный вектор Тогда уравнение плоскости Нормирующий множитель для общего уравнения плоскости Осталось воспользоваться формулой для вычисления расстояния от точки Это и есть искомое расстояние между заданными скрещивающимися прямыми.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 634; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.239.65 (0.007 с.) |

 .
.

 некоторой точки М1, лежащей на прямой a, и получимнормальное уравнение плоскости
некоторой точки М1, лежащей на прямой a, и получимнормальное уравнение плоскости  , то мы сможем вычислить расстояние
, то мы сможем вычислить расстояние 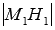 от точки
от точки  до плоскости
до плоскости  (эта формула была получена в статьенахождение расстояния от точки до плоскости). А это расстояние равно искомому расстоянию между скрещивающимися прямыми.
(эта формула была получена в статьенахождение расстояния от точки до плоскости). А это расстояние равно искомому расстоянию между скрещивающимися прямыми. некоторой точки М2, через которую проходит плоскость
некоторой точки М2, через которую проходит плоскость  , то мы сможем написать общее уравнение плоскости
, то мы сможем написать общее уравнение плоскости  .
.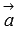 ), и направляющему вектору прямой b (обозначим его
), и направляющему вектору прямой b (обозначим его  ). Тогда в качестве вектора
). Тогда в качестве вектора  можно взять векторное произведение векторов
можно взять векторное произведение векторов  . Определив координаты
. Определив координаты  и
и  направляющих векторов прямых a и b и вычислив
направляющих векторов прямых a и b и вычислив  , мы найдем координаты
, мы найдем координаты  нормального вектора
нормального вектора  , а прямую b – канонические уравнения прямой в пространстве
, а прямую b – канонические уравнения прямой в пространстве  . Найдите расстояние между заданными скрещивающимися прямыми.
. Найдите расстояние между заданными скрещивающимися прямыми. и имеет направляющий вектор
и имеет направляющий вектор  . Прямая b проходит через точку
. Прямая b проходит через точку  , а ее направляющим вектором является вектор
, а ее направляющим вектором является вектор  .
.
 .
. :
:
 равен
равен  . Следовательно, нормальное уравнение этой плоскости имеет вид
. Следовательно, нормальное уравнение этой плоскости имеет вид  .
.



