
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операции над векторами в координатной формеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим в пространстве прямоугольную декартову систему координат (ПДСК)
Разложение вида
называется разложением вектора Введя координаты вектора, можно определить линейные операции над векторами в координатной форме. Пусть
Векторы
Пример. Даны векторы Решение. Согласно формулам имеем
Итак, вектор Вектор
Очевидно, что это условие не выполняется:
Длину вектора можно найти по формулам:
Рассмотрим задачу деления отрезка в заданном отношении. Пусть точка
или в координатной форме
Если точка
Лекция 3 Понятие линейной зависимости и независимости системы векторов. Основные критерии (свойства) линейной зависимости, Независимости системы векторов Определение 1. Векторы
выполняется только при условии
Теорема 1. Система ненулевых векторов зависима тогда и только тогда, когда некоторый вектор линейно выражается через остальные. Доказательство. а) Пусть векторы
то есть вектор б) Пусть какой-то из векторов линейно выражается через остальные, например, вектор
тогда Теорема 2. Для того, чтобы два вектора были линейно зависимыми, необходимо и достаточно, чтобы они были коллинеарными. Доказательство. а) Пусть векторы б) Пусть векторы Теорема 3. Для того, чтобы три вектора были линейно зависимыми, необходимо и достаточно, чтобы они были компланарными. Доказательство. а)Пусть векторы б) Пусть векторы
что векторы линейно зависимы; если векторы
линейно зависимы.
Определение 2. Совокупность линейно независимых векторов таких, что любой вектор линейно выражается через эти векторы, называется базисом. Из приведенных теорем следует, что на плоскости базисом могут быть любые два неколлинеарных вектора, в пространстве базисом могут служить любые три некомпланарных вектора. Если векторы
тогда числа Лекция 4
|
||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 778; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.99.39 (0.007 с.) |

 (см. рис. 3) и в ней вектор
(см. рис. 3) и в ней вектор  .
.
 рассмотрим соответственно единичные векторы
рассмотрим соответственно единичные векторы 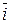 ,
,  ,
,  (
(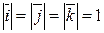 ,
, 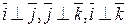 ), которые назовем ортами ПДСК
), которые назовем ортами ПДСК  вектора
вектора  .
.

 (4.1)
(4.1) по базису
по базису  ,
, 
 – векторы, заданные своими координатами. Тогда
– векторы, заданные своими координатами. Тогда
 ,
,
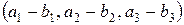 ,
,
 ,
,
 .
. (
( – коэффициент пропорциональности). (4.2)
– коэффициент пропорциональности). (4.2) ,
,  ,
, 
 . Найти координаты вектора
. Найти координаты вектора  . Проверить, являются ли коллинеарными (параллельными) векторы
. Проверить, являются ли коллинеарными (параллельными) векторы  .
. 2
2 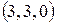 –3
–3  +
+  = =
= =  –
–  .
.
 , вектор
, вектор  . Составляем условие (4.2) и проверим, будет ли оно выполняться или нет для векторов
. Составляем условие (4.2) и проверим, будет ли оно выполняться или нет для векторов  .
.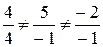 , значит, векторы
, значит, векторы  Пусть заданы координаты начальной и конечной точек вектора, надо найти координаты вектора. Начальная точка
Пусть заданы координаты начальной и конечной точек вектора, надо найти координаты вектора. Начальная точка  , конечная точка ─
, конечная точка ─ 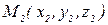 .
.  , следовательно,
, следовательно,  .
.

 делит отрезок так, что
делит отрезок так, что или
или  , тогда
, тогда ,
, 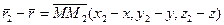 , отсюда следует, что
, отсюда следует, что , если из этого равенства выразить
, если из этого равенства выразить  , получим формулу
, получим формулу


 , то
, то .
.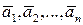 называются линейно независимыми, если равенство
называются линейно независимыми, если равенство (1)
(1) . Если в равенстве (1) хотя бы один из коэффициентов отличен от нуля, то векторы
. Если в равенстве (1) хотя бы один из коэффициентов отличен от нуля, то векторы  называются линейно зависимыми.
называются линейно зависимыми.
 .В этом случае получаем
.В этом случае получаем ,
, линейно выражается через остальные.
линейно выражается через остальные. ,
, , коэффициент при
, коэффициент при  и
и  линейно зависимы, тогда один из векторов линейно выражается через другой, например,
линейно зависимы, тогда один из векторов линейно выражается через другой, например,  , а это и означает, что векторы коллинеарны.
, а это и означает, что векторы коллинеарны. , коэффициент при
, коэффициент при 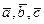 линейно зависимы, тогда один из них линейно выражается через остальные, например,
линейно зависимы, тогда один из них линейно выражается через остальные, например,  , отнесем эти векторы к одному началу, проведем через векторы
, отнесем эти векторы к одному началу, проведем через векторы  , тогда векторы
, тогда векторы  и
и 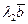 будут тоже принадлежать этой плоскости, следовательно, вектор
будут тоже принадлежать этой плоскости, следовательно, вектор 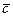 принадлежит плоскости
принадлежит плоскости  , значит вектор
, значит вектор 
 линейно выражается через эти векторы, то есть
линейно выражается через эти векторы, то есть ,
, являются координатами вектора
являются координатами вектора  .
.


