Модели регрессии, нелинейные по оцениваемым коэффициентам

Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели β0…βn.

К моделям регрессии, нелинейными по оцениваемым параметрам, относятся:

1) степенная функция:

2) показательная или экспоненциальная функция:

3) логарифмическая парабола:

4) экспоненциальная функция:

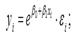
5) обратная функция:

6) кривая Гомперца:

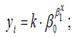
7) логистическая функция или кривая Перла-Рида:

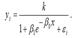
Кривыми насыщения называются показательная, логарифмическая и экспоненциальная функции, т. к. будущий прирост результативной переменной зависит от уже достигнутого уровня функции.

Кривые насыщения применяются для характеристики явлений и процессов, величина роста которых является ограниченной величиной (например, в демографии).

Определение. S-образными кривыми называются кривая Гомперца и кривая Перла-Рида. Данные кривые представляют собой кривые насыщения с точкой перегиба.

S-образные кривые применяются для характеристики явлений, включающий в себя два последовательных процесса – ускорения и замедления достигнутого уровня развития. Подобные явления характерны для демографии, страхования и других областей.

Модели регрессии, нелинейные по оцениваемым коэффициентам, делятся на два класса:

1) модели регрессии, которые можно с помощью преобразований привести к линейному виду;

2) модели регрессии, которые невозможно привести к линейному виду.

Рассмотрим первый класс моделей регрессии.

Показательная функция вида

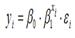
является нелинейной по коэффициенту β1 и относится к классу моделей регрессии, которые можно с помощью преобразований привести к линейному виду. Данная модель характеризуется тем, что случайная ошибка εi мультипликативно связана с факторной переменной хi.

Данную модель можно привести к линейному виду с помощью логарифмирования:

Log yi=log β0+ хi* logβ1+ logεi.

Для более наглядного представления данной модели регрессии воспользуемся методом замен:

log yi=Yi;

log β0=A;

logβ1=B;

logεi=E.

В результате произведённых замен получим окончательный вид показательной функции, приведённой к линейной форме:

Yi=A+Bхi+E.

Таким образом, можно сделать вывод, что рассмотренная показательная функция является внутренне линейной, поэтому оценки неизвестных параметров её линеаризованной формы можно рассчитать с помощью классического метода наименьших квадратов.

Другим примером моделей регрессии первого класса является степенная функция вида:

Данная модель характеризуется тем, что случайная ошибка βi мультипликативно связана с факторной переменной хi.

Данную модель можно привести к линейному виду с помощью логарифмирования:

lnyi=lnβ0+β1 lnхi + lnεi.

Для более наглядного представления данной модели регрессии воспользуемся методом замен:

ln yi=Yi;

ln β0=A;

lnхi=Xi;

lnεi=E.

В результате произведённых замен получим окончательный вид показательной функции, приведённой к линейной форме:

Yi=A+β1Xi+E.

Таким образом, можно сделать вывод, что рассмотренная степенная функция является внутренне линейной, поэтому оценки неизвестных параметров её линеаризованной формы можно рассчитать с помощью классического метода наименьших квадратов.

Рассмотрим второй класс моделей регрессии, нелинейных по оцениваемым коэффициентам.

Показательная функция вида

относится к классу моделей регрессии, которые невозможно привести к линейной форме путём логарифмирования. Данная модель характеризуется тем, что случайная ошибка βi аддитивно связана с факторной переменной хi.

Степенная функция вида

относится к классу моделей регрессии, которые невозможно привести к линейной форме путём логарифмирования. Данная модель характеризуется тем, что случайная ошибка εi аддитивно связана с факторной переменной хi.

Таким образом, для оценки неизвестных параметров моделей регрессии, которые нельзя привести к линейному виду, нельзя применять классический метод наименьших квадратов. В этом случае используются итеративные процедуры оценивания (квази-ньютоновский метод, симплекс-метод, метод Хука-Дживса, метод Розенброка и др.).